1) На произвольном расстоянии от проекции А′B′ проводим новую ось проекций Х1.
2) Чтобы построить на новой плоскости П2′ проекции точек А и В необходимо из точек А′ и B′ провести линии связи к новой оси проекций Х1.
3) На этих линиях связи на П2′, от новой оси Х1 откладываем отрезки, измененные от старой оси Х до точек, расположенных на П2 и получаем проекции А1′′ и В1′′.
4) Соединяем эти точки, получаем натуральную величину прямой.
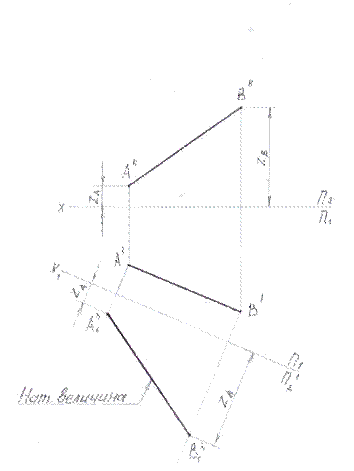
Рисунок 15
3.3 Контрольное задание № 2
1) По данным координатам (таблица 2) построить проекции плоскости и прямой.
2) Найти точку пересечения К прямой CD с плоскостью АВС
3) Определить видимость прямой.
4) Построить натуральную величину отрезка АВ способом перемены плоскостей.
3.3.1 Указания к решению контрольного задания
(Образец выполнения – рисунок 16)
1) Чертеж выполняется на формате А – 3.
2) Изучить темы
а) Ортогональные проекции точки.
б) Построение проекций точки по данным координатам.
3) Согласно своим вариантам, построить проекции плоскости и прямой.
4) Найти точку пересечения К прямой СD и плоскости АВС, согласно подразделу 3.1 данного пособия.
5) Определить видимость прямой, используя конкурирующие точки.
6) Найти натуральную величину отрезка АВ, изучив подраздел 3.2 данного пособия.
Таблица 2 – Исходные данные к контрольному заданию №2
| № варианта | Точки |
Координаты
| № варианта | Точки |
Координаты
| ||||
| Х | Y | Z | Х | Y | Z | ||||
| 1 | A | 145 | 80 | 105 | 6 | A | 120 | 110 | 100 |
| B | 100 | 0 | 20 | B | 70 | 10 | 15 | ||
| C | 10 | 40 | 0 | C | 20 | 65 | 70 | ||
| D | 90 | 80 | 10 | D | 130 | 0 | 50 | ||
| E | 30 | 10 | 65 | E | 10 | 85 | 50 | ||
| 2 | A | 120 | 50 | 0 | 7 | A | 90 | 90 | 110 |
| B | 0 | 75 | 55 | B | 130 | 10 | 70 | ||
| C | 70 | 20 | 90 | C | 15 | 15 | 15 | ||
| D | 30 | 40 | 20 | D | 120 | 0 | 105 | ||
| E | 120 | 80 | 75 | E | 40 | 60 | 15 | ||
| 3 | A | 130 | 70 | 60 | 8 | A | 125 | 80 | 60 |
| B | 80 | 10 | 10 | B | 60 | 10 | 15 | ||
| C | 10 | 70 | 100 | C | 20 | 60 | 100 | ||
| D | 120 | 90 | 10 | D | 125 | 10 | 35 | ||
| E | 40 | 10 | 110 | E | 20 | 80 | 75 | ||
| 4 | A | 120 | 130 | 0 | 9 | A | 130 | 80 | 70 |
| B | 70 | 0 | 130 | B | 50 | 10 | 0 | ||
| C | 20 | 60 | 50 | C | 20 | 80 | 70 | ||
| D | 120 | 25 | 40 | D | 120 | 110 | 20 | ||
| E | 0 | 90 | 120 | E | 45 | 10 | 85 | ||
| 5 | A | 140 | 20 | 20 | 10 | A | 120 | 130 | 50 |
| B | 90 | 120 | 120 | B | 60 | 50 | 0 | ||
| C | 35 | 50 | 60 | C | 5 | 80 | 90 | ||
| D | 155 | 45 | 90 | D | 110 | 60 | 95 | ||
| E | 10 | 100 | 30 | E | 15 | 110 | 10 | ||
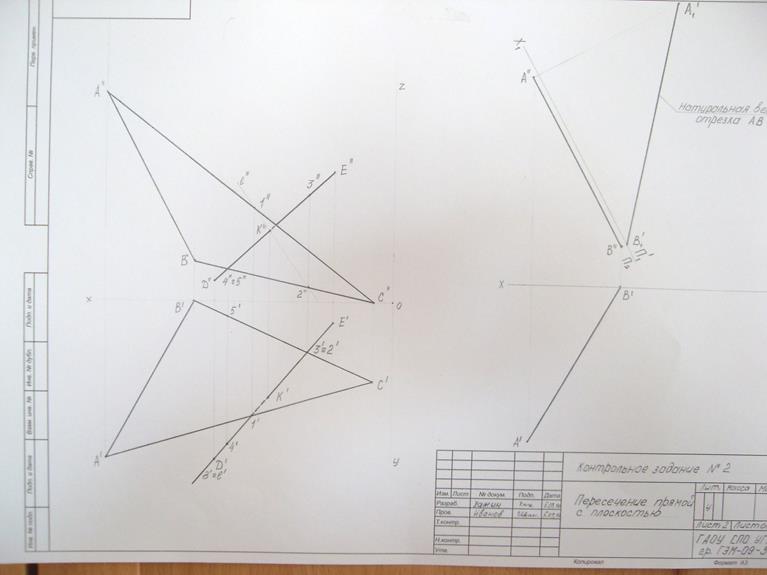
Рисунок 16
Пересечение поверхностей геометрических тел проецирующими плоскостями. Построение ортогональных проекций, линий среза, аксонометрических проекций и разверток поверхностей усеченных геометрических тел
Линии среза – линия пересечения поверхности геометрического тела с секущей плоскостью, а фигура среза (срез) – это плоская фигура, одновременно принадлежащая геометрическому телу и плоскости, которая его пересекает.
При построении геометрических тел со срезами условимся, что отсеченная плоскостью часть геометрического тела отбрасывается, а оставшуюся усеченную часть геометрического тела ограничивает фигура среза (срез).
Сечение поверхностей проецирующей плоскостью
При изучении этой темы необходимо ознакомиться с понятиями контура и очерка поверхности, а так же с вариантами прямых и кривых линий, получающихся в результате сечения поверхностей плоскостью.
Дата: 2018-12-28, просмотров: 339.