При пересечении тела вращения плоскостью контур пересечения будет представлять собой замкнутую кривую линию, форма которой зависит от:

- формы тела вращения;

- положения секущей плоскости.

На рисунках 17 и 18 изображены примеры пересечения фигур плоскостями.

Для построения этой линии необходимо построить ряд точек, которые будут принадлежать и поверхности тела и плоскости.

          Построение следует начинать с габаритных точек. К таким точкам относятся:

- габаритные точки, определяющие наибольшие размеры линии пересечения по высоте и ширине;

- точки, лежащие на крайних образующих и образующих, проекции которых совпадают с осевыми линиями.

Построив характерные точки, строят промежуточные, используя для этого в качестве вспомогательных линий прямые – образующие или окружности (меридианы и параллели).

Строя линию пересечения, необходимо знать, по какой кривой пересекаются тела вращения.

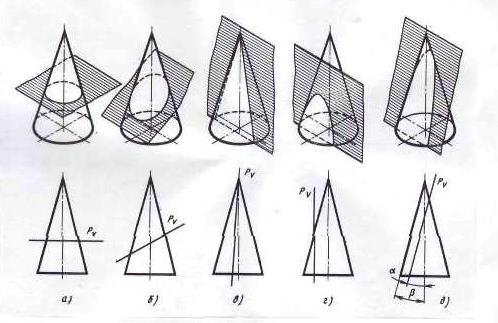
Рисунок 17 – Пересечение конуса плоскостями

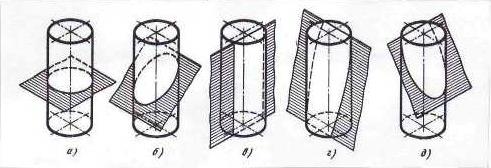
Рисунок 18 – Пересечение цилиндра плоскостями

В сечении шара любой плоскостью получается окружность. Если эта окружность лежит в плоскости уровня, то она проецируется на соответствующую плоскость проекции без искажения, т.е. строится с помощью циркуля и для её построения достаточно знать центр и радиус. Если окружность лежит в плоскости, не параллельной плоскости проекций, то она при проецировании искажается в эллипс, для построения которого необходимо отметить характерные точки:

a) соответствующие концам большой и малой осей эллипса

b) лежащие на очерках сферы, а так же промежуточные точки.

4.1.2 Построение пересечения конуса проецирующей плоскостью. Определение натуральной величины фигуры сечения (рисунок 19)

Алгоритм решения задачи:

1) Строим в тонких линиях ортогональные проекции конуса;

2) На П₂ вычерчиваем проекцию секущей горизонтально-проецирующей плоскости ;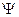

3) Определяем название линии сечения – это эллипс;

4) На П₂ отмечаем характерные точки линии;

- a", b" – концы большой оси;

- с" и с₁" – концы малой оси; они располагаются в середине отрезка 1" – 2";

- d" и d₁" – точки на профильном контуре конуса;

5) Строим отмеченные точки на П₁

- 1' и 2' – по принадлежности к фронтальному контуру;

- с'с₁' и d'd₁' – с помощью параллелей;

6) Профильные проекции данных точек строим, используя линии проекционной связи.

7) Для построения промежуточных точек эллипса, а в дальнейшем и для построения развертки конуса проводим на его поверхности дополнительные образующие. Для этого:

- на П₁ делим основание конуса на 12 равных частей;

- из полученных точек проводим проекции 12 образующих на П₁ и П₂;

- на П₂ находим точки пересечения фрактально-проецирующей плоскости 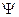 с дополнительными образующими;

 - затем с помощью линии проекционной связи строим их на П₁ и П₃.

8) Соединяем полученные точки с учетом видимости и обводим контур фигуры, оставшийся от сечения тела плоскостью.

9) Для построения натуральной величины фигуры среза применен способ вращения.

- вращаем плоскость 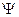 вокруг фронтально-проецирующей оси 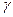" до положения горизонтального уровня 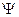₁";

- при этом все точки линии сечения на П₂ движутся по окружности с центром ";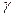

- на П₁ плоскости вращения точек перпендикулярны '.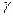

10) Точки фигуры среза получаем в результате пересечения линий проекционной связи, идущих из точек среза на П₁ и точек расположенных на 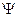₁".

11) Соединяем полученные точки и получаем натуральную величину фигуры среза

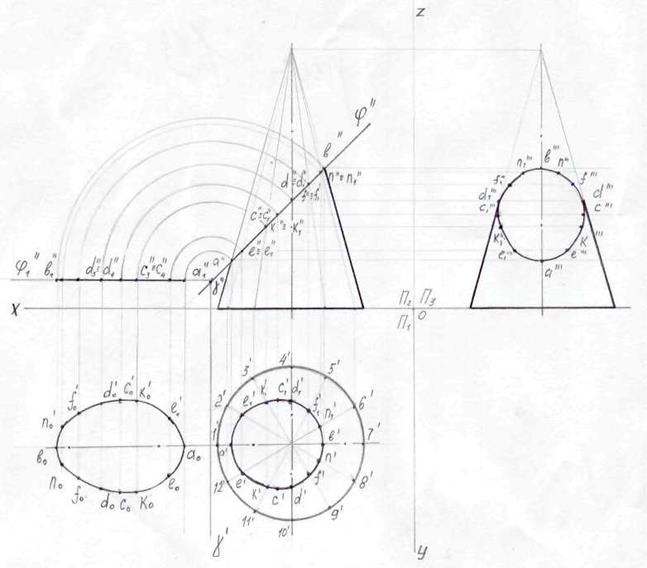
Рисунок 19