Деление с восстановлением остатка является аритмичным процессом с переменным числом шагов внутри циклов в зависимости от того, произошла или нет инверсия знака сумматора при очередном подсуммировании делителя. С этим связаны дополнительные затраты времени на выполнение операции. Операцию можно видоизменить таким образом, чтобы в каждом такте выполнялось два шага.
Рассмотрим случай, когда очередной остаток (при делении модулей операндов) отрицательный, Ri<0. В предыдущем алгоритме в этом случае выполнялись следующие операции.
· Восстановление остатка:
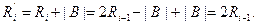
· Сдвиг восстановленного остатка влево:
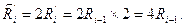
· Вычитание модуля делителя из восстановленного и сдвинутого влево остатка для определения следующего остатка:
Ri+1=4Ri-1 - |B|.
Если не восстанавливать остаток, а сразу сдвинуть отрицательный остаток влево на один разряд, то получим
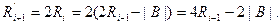
Результат в этом случае отличается от действительного на величину +|B|. Поэтому в качестве второго шага необходимо произвести коррекцию результата на эту величину:
Ri+1=4Ri-1 - 2´|B|+|B|=4Ri-1 - |B|.
В результате получаем требуемую величину последующего остатка Ri+1 за два шага.
Таким образом, чтобы определить следующую цифру частного, необходимо сдвинуть текущий остаток влево на один разряд, а затем алгебраически прибавить к нему модуль делителя. Заметим, что при делении на сумматоре всегда складываются числа с противоположными знаками, т.е. всегда производится вычитание.
Сдвиги и вычитания производятся до тех пор, пока не будет получено требуемое число разрядов частного. В схеме операционного автомата для контроля числа полученных разрядов частного используется счетчик, в который в начале выполнения операции деления записывается число, на 1 большее числа определяемых разрядов частного. Это делается для того, чтобы так называемое пробное деление выполнялось в общем цикле. При этом старший разряд частного – псевдознаковый разряд. Он не несет информацию о знаке частного, а является критерием переполнения разрядной сетки частного. Так как мантиссы делимого и делителя являются нормализованными, т.е. 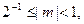 диапазон возможных значений частного составляет
диапазон возможных значений частного составляет
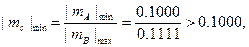
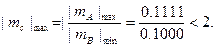
В последнем случае в псевдознаковом разряде частного оказывается 1, которая и означает переполнение разрядной сетки.
Пусть С=А/В, А=-0,10101, В=0,11010. Дополнительные модифицированные коды делимого и делителя равны соответственно: 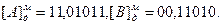 Пример деления приведен в таблице 16.
Пример деления приведен в таблице 16.
Таблица 16 Деление двоичных чисел с фиксированной запятой без восстановления остатка со сдвигом текущего остатка
| СМ | РгС | СТ | Комментарии |
| 00,00000 +11,01011 11,01011 +00,11010 00,00101 | - - - - - - | 6 | СМ:=0, РгА:= 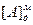 , РгВ:= , РгВ:= 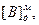 ТП:=0, СТ:=6, ТП:=0, СТ:=6,
|
| СМ:=СМ+РгА, | |||
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| - - - - - 0 | 5 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, | |
| 00,01010 +11,00110 11,10000 | - - - - 0 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
SgСМ=SgРгВ? ДА. Следовательно, 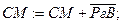
| |||
| - - - - 01 | 4 | SgСМ=SgРгА? ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 11,00000 +00,11010 11,11010 | - - -01 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| - - - 011 | 3 | SgСМ=SgРгА? ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 11,10100 +00,11010 00,01110 | - - 011 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| - - 0110 | 2 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, | |
| 00,11100 +11,00110 00,00010 | - 0110 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
SgСМ=SgРгВ? ДА. Следовательно, 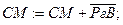
| |||
| - 01100 | 1 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, | |
| 00,00100 +11,00110 11,01010 | 01100 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
SgСМ=SgРгВ? ДА. Следовательно, 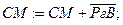
| |||
| 011001 | 0 | СТ=0? ДА. Выход из цикла. Проверяем переполнение разрядной сетки: РгС[0]=1? НЕТ. Следовательно, переполнение разрядной сетки отсутствует. | |
| Далее определяем значение знака частного. SgAÅSgB=1, следовательно, полученный результат необходимо инвертировать, используя при этом сумматор. Окончательно частное будет иметь вид: [mc ]д =1.00111. |
Результат деления получается одинаковым, если сдвигать остатки от деления влево или сдвигать делитель вправо. В первом случае при делении необходимо использовать модифицированные коды, так как при сдвиге текущего остатка влево может возникнуть переполнение разрядной сетки сумматора, которое исчезнет при следующем подсуммировании делителя. Во втором случае использовать модифицированные коды не надо, так как переполнение разрядной сетки возникнуть в принципе не может, поскольку в сложении всегда участвуют числа с разными знаками.
Рассмотрим пример деления двоичных чисел с фиксированной запятой без восстановления остатка со сдвигом делителя вправо.
Пусть С=А/В, А=-0,10101, В=0,11010. Дополнительные модифицированные коды делимого и делителя равны соответственно:
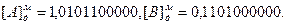 Пример деления приведен в таблице 17.
Пример деления приведен в таблице 17.
Таблица 17 Деление двоичных чисел с фиксированной запятой со сдвигом делителя без восстановления текущего остатка
| СМ | РгВ | РгС | СТ | Комментарии |
| 0,00000 00000 +1,01011 00000 1,01011 00000 +0,11010 00000 0,00101 00000 | 0,11010 00000 | - - - - - - | 6 | СМ:=0, РгА:= 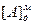 , РгВ:= , РгВ:= 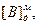 ТП:=0, СТ:=6, ТП:=0, СТ:=6,
|
| СМ:=СМ+РгА, | ||||
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | ||||
| - - - - - 0 | 5 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, | ||
| 0,00101 00000 +1, 10011 00000 1,11000 00000 | 0.01101 00000 | - - - - 0 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, РгВ:=R(1) РгВ, | |
SgСМ=SgРгВ? ДА. Следовательно, 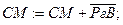
| ||||
| 0,00110 10000 | - - - - 01 | 4 | SgСМ=SgРгА? ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 1,11000 00000 +0,00110 10000 1,11110 10000 | - - -01 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, РгВ:=R(1) РгВ, | ||
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | ||||
| - - - 011 | 3 | SgСМ=SgРгА? ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | ||
| 1,11110 10000 +0,00011 01000 0,00001 11000 | 0,00011 01000 | - - 011 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, РгВ:=R(1) РгВ, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | ||||
| - - 0110 | 2 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, | ||
| 0,00001 11000 +1,11110 01100 0,00000 00100 | 0,00001 10100 | - 0110 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, РгВ:=R(1) РгВ, | |
SgСМ=SgРгВ? ДА. Следовательно, 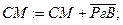
| ||||
| - 01100 | 1 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, | ||
| 0,00000 00100 +1,11111 00110 1,11111 01010 | 01100 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, РгВ:=R(1) РгВ, | ||
SgСМ=SgРгВ? ДА. Следовательно, 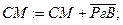
| ||||
| 011001 | 0 | СТ=0? ДА. Выход из цикла. Проверяем переполнение разрядной сетки: РгС[0]=1? НЕТ. Следовательно, переполнение разрядной сетки отсутствует. | ||
| Далее определяем значение знака частного. SgAÅSgB=1, следовательно, полученный результат необходимо инвертировать, используя при этом сумматор. Окончательно частное будет иметь вид: [mc ]д =1.00111. |
Для реализации рассмотренной схемы деления понадобятся два регистра и сумматор с двойной точностью. Все остальные структурные элементы операционного автомата те же, что и при делении со сдвигом текущего остатка.
Деление всегда выполняется на сумматоре инверсного кода (дополнительного или обратного). Операционный автомат, выполняющий деление двоичных чисел с плавающей запятой, является составной частью процессора, который решает также задачи умножения и сложения. Выбор схемы деления зависит от способа реализации умножения с плавающей запятой. Так как быстродействие процессора зависит от наличия необходимого количества регистров в сверхбыстрой регистровой памяти процессора, целесообразно выбирать обе схемы таким образом, чтобы для них использовались одни и те же регистры с соответствующими направлениями сдвигов.
[1] Савельев А.Я. Прикладная теория цифровых автоматов. М.: «Высшая школа», 1987
[2] Самофалов К.Г. и др. Прикладная теория цифровых автоматов. Киев: «Вища школа», 1987. – 375 с.
Дата: 2018-12-28, просмотров: 451.