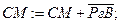Прежде всего, необходимо отметить, что при делении чисел с фиксированной запятой цифры частного вычисляются в прямом или обратном коде. Знак результата при делении определяется как сумма по модулю 2 знаков делимого и делителя. Знак присваивается результату в конце выполнения операции деления. Деление выполняется всегда в инверсном коде. Поэтому, при отсутствии переполнения разрядной сетки частного положительный результат может передаваться в память непосредственно из регистра частного, так как в этом случае в псевдознаковом разряде находится 0. Если же результат деления отрицательный, то передача его в память должна производиться в том коде, в котором данные поступили на обработку из памяти (дополнительном или обратном). В случае обратного кода это означает необходимость инвертирования всего содержимого регистра частного, включая псевдознаковый разряд. Если же операция деления выполнялась в дополнительном коде, то получение инверсного кода требует использования сумматора из-за необходимости подсуммирования единицы в младший разряд инверсного кода числа, находящегося в регистре частного.
Рассмотрим алгоритм деления на примере деления модулей операндов. Пусть А – делимое, В – делитель. Требуется разделить А на В с точностью до i-го разряда. Тогда
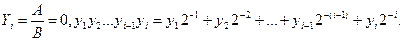
| (14) |
При любом значении I должно выполняться неравенство
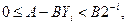
| (15) |
т.е. остаток от деления A - BYi должен быть меньше делителя, умноженного на 2-i. Преобразуем (2) к виду
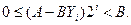
| (16) |
Обозначив (A – BYi)2i=Ri, получим
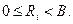
| (17) |
Цифры частного определяются последовательно, начиная со старшего разряда. Допустим, что в результате выполнения i циклов получены i старших разрядов частного, т.е. приближенное значение частного Yi, удовлетворяющие неравенству (17). В следующем (i +1)м цикле будет получено значение (i +1) – го разряда частного. Исходными данными для этого цикла являются Yi и Ri.
Цифра yi +1 принимает значение в множестве {0,1}. Если yi+1=0, то
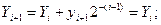
| (18) |
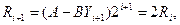
| (19) |
т.е. в частном записывается 0 при условии
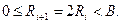
| (20) |
Если yi+1=1, то
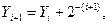
| (21) |
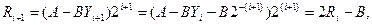
| (22) |
т.е. цифра частного равна 1, если выполняется условие
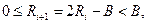
| (23) |
или
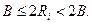
| (24) |
Так как всегда выполняется одно из условий (20) или (24), то для определения текущей цифры частного достаточно проверить одно из них. Обычно проверяют условие (20). Левая часть этого неравенства выполняется заведомо, так как согласно (17) 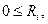 т.е. очередной остаток перед началом следующего шага деления – всегда положительное число.
т.е. очередной остаток перед началом следующего шага деления – всегда положительное число.
Для проверки правой части неравенства сравним разность (2 Ri – B ) с нулем. Если эта разность окажется отрицательной, то в ( i +1)–й разряд частного запишем 0 и для подготовки исходных данных для ( i +2)-го цикла определим Ri+1 следующим образом:
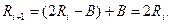
(12)
Если разность 2 Ri - B >0 то запишем в ( i +1)-разряд частного 1, а в качестве исходного значения для следующего (i +2)-го цикла используем вычисленную разность Ri +1 =2 Ri – B.
Исходными данными для 1-го цикла являются Y 0 =0, R 0 =( A - BY 0 )20= A < B, т.е. неравенство (17) выполняется и перед началом первого цикла. После завершения n-го цикла мы получим n -значное частное Yn, вычисленное с недостатком. Таким образом, правило деления с восстановлением остатков формулируется следующим образом. Делитель вычитается из делимого и определяется знак остатка. Если остаток положительный (делим модули операндов), в псевдознаковом разряде записывается 1. В противном случае в псевдознаковый народ записываем 0, а затем производим восстановление остатка путем подсуммирования делителя к текущему остатку. Далее выполняется сдвиг восстановленного остатка на один разряд влево и повторное вычитание делителя. В рассматриваемом случае цифры частного получаются как инверсное значение знака текущего остатка.
Правила, в соответствии с которыми определяется знак подсуммирования делителя к текущему остатку и определяется очередная цифра частного, приведены в таблице 14.
Таблица 14 Действия, выполняемые при делении мантисс
| SgA | 0 | 0 | 1 | 1 | |||||
| SgB | 0 | 1 | 0 | 1 | |||||
| СМ | ³0 | <0 | ³0 | <0 | >0 | £0 | >0 | £0 | |
| Действие на СМ | +(ØB) | +B | +B | +(ØB) | +(ØB) | +B | +B | +(ØB) | |
| Цифра частного | ПК | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| ОК | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
Для выполнения операции деления мантисс требуются следующие структурные элементы ОА:
· 2 регистра для хранения делимого и делителя в модифицированном коде;
· сумматор ДСДК (ДСОК), согласованный по формату с регистрами операндов;
· инвертор, для инверсии делителя, так как на сумматоре всегда складываются числа с разными знаками;
· счетчик, задающий число вычисляемых разрядов частного;
· триггер прерывания, который устанавливается в 1, если значение делителя равно 0;
· комбинационные схемы, определяющие значение очередной цифры частного, знак результат, знак подсуммирования делителя в текущем такте.
Пример деления двоичных чисел с фиксированной запятой на ДСДК со сдвигом текущего остатка с восстановлением остатка
Пусть С=А/В, А=-0,11101, В=0,100010. Дополнительные модифицированные коды делимого и делителя равны соответственно: 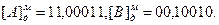 Пример деления приведен в таблице 15.
Пример деления приведен в таблице 15.
Таблица 15 Деление со сдвигом текущего остатка с восстановлением остатка
| СМ | РгС | СТ | Комментарии |
| 00,00000 | - - - - - - | 6 | СМ:=0, РгА:= 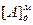 , РгВ:= , РгВ:= 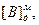 ТП:=0, СТ:=6, ТП:=0, СТ:=6,
|
| +11,00011 11,00011 +00,10010 11,10101 | СМ:=СМ+РгА, | ||
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| - - - - - 1 | 5 | SgСМ=SgРгА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 11,01010 +00,10010 11,11100 | - - - - 1 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ Следовательно, СМ:=СМ+РгВ, | |||
| - - - - 11 | 4 | SgСМ=SgРгА. ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 11,11000 +00,10010 00,01010 | - - - 11 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| - - - 110 | 3 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, Знак сумматора в этом такте инвертировался. Производится восстановление остатка. SgСМ=SgРгВ? ДА. Следовательно, | |
| 00,01010 +11,01110 11,11000 | |||
| 11,10000 +00,10010 00,00010 | - - 110 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| 00,00010 +11,01110 11,10000 | - - 1100 | 2 | SgСМ=SgРгА? НЕТ. Следовательно, РгС[5]:=0, СТ:=СТ-1, Знак сумматора в этом такте инвертировался. Производится восстановление остатка.
SgСМ=SgРгВ? ДА. Следовательно, 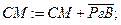
|
| 11,00000 +00,10010 11,10010 | - 1100 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| - 11001 | 1 | SgСМ=SgРгА. ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 11,00100 +00,10010 11,10110 | 11001 - | СТ=0? НЕТ. Следовательно, РгС:=L(1) РгС, СМ:=L(1) CM, | |
| SgСМ=SgРгВ? НЕТ. Следовательно, СМ:=СМ+РгВ, | |||
| 110011 | 0 | SgСМ=SgРгА. ДА. Следовательно, РгС[5]:=1, СТ:=СТ-1, | |
| 011001 | СТ=0? ДА. Выход из цикла. Проверяем переполнение разрядной сетки: РгС[0]=1? ДА. Следовательно, переполнение разрядной сетки частного имеет место. Выполняем нормализацию результата. С этой целью мантиссу сдвигаем логическим сдвигом на один разряд вправо, и к порядку прибавляем 1. Младший разряд частного сваливается с разрядной сетки и теряется. РгС:=R(1)РгС; СМП:=СМП+1; (Операции над порядком в этой таблице не отображены). |
Далее проверяется значение знакового разряда частного, который определяется с помощью комбинационной схемы как сумма по модулю 2 знаков делимого и делителя. Если результат положительный, то результатом деления мантисс является содержимое регистра С и значение порядка, которое находится в сумматоре порядка. Если же результат деления отрицательный, то его необходимо инвертировать перед отправлением результата в память. При использовании обратного кода достаточно проинвертировать результат с помощью имеющегося сумматора. В случае деления на ДСДК для получения инверсного кода частного придется использовать сумматор для подсуммирования 1 в младший разряд инверсного кода. При этом необходимо обратить внимание на согласование форматов регистра С и сумматора.
Дата: 2018-12-28, просмотров: 413.