При умножении сомножители играют разную роль: множимое подсуммируется к накопленным значениям частичного произведения. А множитель управляет процессом подсуммирования. Порядок выполнения действий и требуемые аппаратные средства определяются схемой Горнера. Результат умножения получается в дополнительном коде с правильным знаком и двойной точности. Схема Горнера э это математическое выражение, представляющее умножение как операцию над значением множимого, когда множитель записан в виде взвешенной суммы значений разрядов. Инверсные коды (дополнительный и обратный) при отрицательном множителе инвертируют значения его разрядов в соответствии с правилами образования соответствующего кода. Поэтому непосредственное умножение «столбиком» на отрицательный множитель приводит к неверному результату. Поэтому прежде, чем рассматривать собственно алгоритм умножения необходимо понять, на что же должно умножаться множимое. В соответствии с вышеизложенным, дополнительный код положительного числа совпадает с его естественным представлением, а в случае отрицательного числа множитель, полученный из памяти, представлен в соответствии с правилом образования дополнительного кода. На основании этого правила необходимо определить то значение множителя В, на которое должно производиться умножение. Итак, при отрицательном множителе B <0 его код, принимаемый из памяти, имеет вид: [ B ]д=р+В. Отсюда
| B =[ B ]д – р = SgB . b 1 b 2 … bn - p . | (3) |
Так как мы рассматриваем случай отрицательного множителя, SgB =1, и единица в знаковом разряде имеет вес 20=1, выражение (1) можно переписать в виде:
| B = 1, b 1 b 2 … bn – 2 = 0, b 1 b 2 … bn +1-2 = 0, b 1 b 2 … bn – 1. | (4) |
Запишем теперь произведение двух двоичных чисел в виде
| [C] д = [A] д (b12-1+b22-2+…+bn2-n-1)=b1([A] д 2-1) + b2([A] д 2-2)+…+bn([A] д 2-n) - SgB[A] д , | (5) |
Из выражения (5) следует, что при умножении по схеме 1 на ДСДК регистр множимого А должен в каждом такте умножения сдвигаться на один разряд вправо; поэтому регистр А должен иметь двойную точность. Такую же точность должен иметь сумматор. Разряды множителя анализируются, начиная со старшего разряда. Поэтому регистр множителя сдвигается влево. Коме того из (5) видно, что, если SgB =1 ( случае отрицательного множителя), в начале умножения необходимо выполнить коррекцию, выполнив микрооперацию
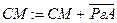. Инверсное значение множимого `А может быть получено с помощью инвертора, который инвертирует все цифры множимого, принятого из памяти. При этом получается обратный код А. Для получения дополнительного кода числа, записанного в РгА, в соответствии с правилом образования дополнительного кода необходимо одновременно подать на вход переноса младшего разряда сумматора 1. При этом обратный код, полученный при инвертировании, становится дополнительным кодом. При положительном множителе SgB =0, и коррекция не выполняется. Таким образом, выражение (5) полностью описывает все этапы выполнения умножения по схеме 1 на ДСДК.
ПРИМЕР
Пусть А=0,1101, В=-0,1011. Требуется определить произведение [C]д = [A]д´В. Последовательность действий в соответствии с формулой (3) представлена в Табл. 6.
Таблица 6 Умножение двоичных чисел с фиксированной запятой на ДСДК, схема 1
| СМ | РгА | РгВ | СТ | Комментарии |
| 0.0000 0000 +1.0011 0000 1.0011 0000 +0.0011 0100 1.0110 0100 +0.0000 1101 1.011 0001 | 0.1101 0000 | 1.0101 | 4 | Такт 1. СМ:=0, РгА:= [A]д|0000, РгВ:= [В]д , СТ:=4 (четыре числовых разряда, которые должны быть проанализированы). |
| Такт 2. Проверка знака В. SgB=1, следовательно, выполняется коррекция: СМ:=СМ+ØРгА+1. | ||||
| 0.0110.1000 | 0101* | Такт 3. РгА:= R(1)РгА, РгВ:=L(1)РгВ, | ||
| 0.0011 0100 | 101** | 3 | Такт 4. Выполняется проверка РгВ[0]=1. Условие не выполняется. Поэтому такт подсуммирования пропускается, выполняются сдвиги и декремент счетчика: РгА:= R(1)РгА, РгВ:=L(1)РгВ, СТ:=СТ-1. | |
| Такт 5. Проверка: СТ=0. Условие не выполняется. Выполняется проверка РгВ[0]=1. Условие выполняется. СМ:=СМ+РгА. | ||||
| 0.0001 1010 | 01*** | 2 | Такт 6. РгА:= R(1)РгА, РгВ:=L(1)РгВ, СТ:=СТ-1. | |
| 0.0000 1101 | 1**** | 1 | Такт 7. Выполняется проверка РгВ[0]=1. Условие не выполняется. Поэтому такт подсуммирования пропускается, выполняются сдвиги и декремент счетчика: РгА:= R(1)РгА, РгВ:=L(1)РгВ, СТ:=СТ-1. | |
| 0 | Такт 8. Проверка: СТ=0. Условие выполняется. Выход из цикла. Конец умножения. |
Чтобы прочесть результат, запишем его в естественной форме: С = - 0.100 1111. Последняя запись получена обратным преобразованием дополнительного кода отрицательного числа в естественную форму представления. Как видно, результат получился автоматически с правильным знаком.
Дата: 2018-12-28, просмотров: 252.
