Введение
Конечные автоматы и такие связанные с ними конструкции как линейные грамматики и регулярные выражения относятся к важнейшим понятиям информатики. Различные варианты конечных автоматов и близкие им математические объекты служат для описания и анализа технических устройств, различных систем и процессов, программ и алгоритмов. Теория автоматов является одним из старейших разделов теоретической информатики.
Хотя теория конечных автоматов изучает очень простые модели, она является фундаментом очень большого числа приложений. Эти приложения – от языковых процессоров до систем управления реального времени и протоколов связи – покрывают значительную долю систем, разработкой, реализацией и анализом которых занимается информатика.
Мнения специалистов, относящиеся к теории автоматов, высказанные на семинаре “Software 2000:
· 80или даже 90% информатики будет в будущем основываться на теории автоматов.
· Я знаю людей из «Боинга», занимающихся системами стабилизации самолетов с использованием теории автоматов. Даже трудно себе представить, что им удалось сделать с помощью этой теории.
· Большая часть теории автоматов была успешно использована в системных программах и текстовых фильтрах в OS UNIX. Это позволяет множеству людей работать на высоком уровне и разрабатывать очень эффективные программы.
В настоящем курсе цифровые автоматы рассматриваются как теоретическая основа проектирования аппаратных средств ЭВМ последовательного типа. В этом случае принято рассматривать цифровой автомат как совокупность операционного автомата (исполнительного устройства) и управляющего автомата (собственно конечного автомата), образующих операционное устройство.
Устройство, исполняющее алгоритм процедурного типа, называется операционным устройством (ОУ). ОУ можно рассматривать как один синхронный автомат со сложно структурированной памятью: часть памяти используется для идентификации шага алгоритма, остальная память используется для запоминания промежуточных данных, вычисляемых в процессе последовательного (по шагам) выполнения алгоритма. Такая модель вычислителя удобна для расчета продолжительности одного такта работы устройства.
УА инициирует последовательность шагов алгоритма в соответствии с алгоритмом выполнения операции. ОА выполняет все вычисления на отдельных шагах алгоритма под управлением УА. Кроме того, к ОА удобно отнести все вычисления предикатов, оставив УА только анализ вычисленных значений предикатов.
Конспект лекций включает разделы, относящиеся к арифметическим основам ЭВМ, основные концепции которых можно найти в учебниках[1],[2]
Каноническое описание синхронного конечного автомата можно интерпретировать как одношаговый алгоритм процедурного типа. Исполнителем этого алгоритма является ОА. На каждом шаге этого алгоритма изменяется вся память устройства, поэтому управление памятью не требуется, нет необходимости идентифицировать шаги этого алгоритма.
Проектирование ОУ включает следующие этапы:
· Изучение алгоритма выполнения операции,
· Определение необходимого состава структурных элементов ОА, таких как, регистры, сумматоры, оригинальные комбинационные схемы;
· Определение необходимых форматов структурных элементов;
· Составление граф схемы алгоритма (ГСА) выполнения операции;
· Построение управляющего автомата.
В ОА выполняются микрооперации над данными, которые поступают из памяти и хранятся в регистрах. Множество регистров образуют сверхбыструю память. Обработка данных в ОУ происходит с минимальным числом обращений к внешней памяти, а именно, обращение к внешней памяти происходит дважды за время работы автомата: первое обращение – получение данных, второе обращение – передача в память результатов обработки. Автомат такого типа называется автоматом с жесткой логикой. В отличие от микропрограммных автоматов, которые выполняют те же функции с обращением к памяти на каждом такте. Так как обращение к внешней памяти требует больших затрат времени по сравнению с обращением к регистровой памяти, автоматы с жесткой логикой имеют повышенное быстродействие. Такие автоматы являются основой RISK – процессоров.
Автомат с жесткой логикой работает в дискретном времени. Поэтому на вход УА поступает синхронизирующий сигнал, который определяет это дискретное время. В каждом такте автоматного времени УА активизирует набор микроопераций, которые выполняются в ОА. Промежуточные результаты обработки данных, а также значения предикатов, отображающих состояния отдельных элементов ОА, хранятся в регистровой памяти ОА.
 |
Микрооперация - базисное (элементарное) действие, необходимое для получения (вычисления) значения одной или более переменных. Микрооперации входят в состав микрооператоров. Микрооператор - набор взаимосвязанных микроопераций (или одна микрооперация), выполняемых одновременно и необходимых для получения одного или более значений.
 |
Микрокоманда - набор сигналов, поступающих из УА в ОА, и интерпретируемый как управляющий, т.е. необходимый для выполнения всех микроопераций данного микрооператора.
Блок схема ОУ приведена на рисунке 1. Здесь:
· Х – множество осведомительных сигналов о состоянии контролируемых элементов ОА.
· У – множество микрокоманд, вырабатываемых в УА в соответствии с ГСА.
· G – команда, инициализирующая процесс выполнения задачи.
· СС – синхронизирующий сигнал.
· КР – сигнал окончания работы ОУ.
Данные, полученные из внешней памяти, обрабатываются только в ОА. Управляющий автомат получает из ОА множество осведомительных сигналов, которые являются внешними переменными УА, и посылает в ОА управляющие сигналы. Управляющий сигнал инициирует выполнение микрокоманды, которая состоит из нескольких (возможно, одной) микроопераций.
Во многих приложениях обычная модель конечного автомата расширяется путем добавления переменных. Это дает возможность объединить наглядность представления состояний и переходов между ними с возможностями языков программирования для описания условий и действий, связанных с переходами. Подобное расширение используется, например, в языке формального описания протоколов и сервисов. Оно положено в основу стандарта UML - универсального моделирующего языка.
Арифметика ЦВМ
Модифицированные коды.
В модифицированных кодах вслед за знаковым разрядом вводится разряд переполнения, имеющий формат цифр используемой системы счисления. Т.е. в двоичной системе счисления разряд переполнения занимает один бит. В десятичной и шестнадцатеричной – четыре бита. В восьмеричной – три бита. При выполнении алгебраического сложения первый знаковый разряд, он обозначается Sg1, всегда сохраняет правильное значение знака результата. Разряд переполнения служит для контроля переполнения разрядной сетки.
В двоичной системе счисления запись числа в модифицированном коде имеет вид:
Sg1 Sg2.c1,c2,…,cn, где c1,c2,…,cn – числовые разряды, Sg1 Sg2 – два знаковых разряда, каждый из которых занимает один бит. Точка между знаковой и числовой частью служит исключительно для удобства чтения чисел, так как в разрядной сетке регистра отсутствует какой-либо разделитель этих двух частей в записи числа. Положение запятой при такой записи обозначается только в пояснениях, которые содержатся в сопровождающей документации.
Критерий переполнения d разрядной сетки формулируется следующим образом:
d =0 Û Sg 1= Sg 2.
Если Sg 1 ¹ Sg 2, и Sg 1=0, говорят о положительном переполнении разрядной сетки.
Если Sg 1 ¹ Sg 2, и Sg 1=1, говорят об отрицательном переполнении разрядной сетки.
При обработке чисел в форме с плавающей запятой положительное переполнение разрядной сетки порядка в результате вычислений сопровождается выработкой требования прерывания. Отрицательное переполнение разрядной сетки порядка не требует прерывания. В этом случае результату присваивается значение 0, порядок и мантисса обнуляются.
При представлении чисел в форме с плавающей запятой данные представляются в нормализованном виде. Допустимые значения нормализованной мантиссы находятся в диапазоне p -1 £ | m | <1.
Если мантисса результата вычислений не удовлетворяет заданному диапазону значений в правой части неравенства, т.е.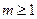 
, говорят о нарушении нормализации справа (переполнении разрядной сетки).. Критерием нарушения нормализации справа является d =1 (d =1 Û Sg 1 ¹ Sg 2).
Переполнение разрядной сетки мантиссы требует выполнения определенных действий: если Sg 1 ¹ Sg 2, необходимо выполнить арифметический сдвиг мантиссы на один разряд вправо и прибавить единицу к значению порядка. Поскольку при сложении двух чисел может произойти переполнение разрядной сетки не более чем на один разряд, процедура нормализации при этом занимает один такт автоматного времени.
Если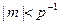 
, говорят о нарушении нормализации слева. Критерием нарушения нормализации слева является величина l.
l =1 Û Sg 2= c 1 , т.е. в случае равенства значений знакового разряда и старшего числового разряда при отсутствии переполнения разрядной сетки. Очевидно, l=1 означает, что значение мантиссы меньше, чем р-1. Для нормализации числа требуется выполнить сдвиг мантиссы на один разряд влево и вычесть 1 из значения порядка.
Введение
Конечные автоматы и такие связанные с ними конструкции как линейные грамматики и регулярные выражения относятся к важнейшим понятиям информатики. Различные варианты конечных автоматов и близкие им математические объекты служат для описания и анализа технических устройств, различных систем и процессов, программ и алгоритмов. Теория автоматов является одним из старейших разделов теоретической информатики.
Хотя теория конечных автоматов изучает очень простые модели, она является фундаментом очень большого числа приложений. Эти приложения – от языковых процессоров до систем управления реального времени и протоколов связи – покрывают значительную долю систем, разработкой, реализацией и анализом которых занимается информатика.
Мнения специалистов, относящиеся к теории автоматов, высказанные на семинаре “Software 2000:
· 80или даже 90% информатики будет в будущем основываться на теории автоматов.
· Я знаю людей из «Боинга», занимающихся системами стабилизации самолетов с использованием теории автоматов. Даже трудно себе представить, что им удалось сделать с помощью этой теории.
· Большая часть теории автоматов была успешно использована в системных программах и текстовых фильтрах в OS UNIX. Это позволяет множеству людей работать на высоком уровне и разрабатывать очень эффективные программы.
В настоящем курсе цифровые автоматы рассматриваются как теоретическая основа проектирования аппаратных средств ЭВМ последовательного типа. В этом случае принято рассматривать цифровой автомат как совокупность операционного автомата (исполнительного устройства) и управляющего автомата (собственно конечного автомата), образующих операционное устройство.
Устройство, исполняющее алгоритм процедурного типа, называется операционным устройством (ОУ). ОУ можно рассматривать как один синхронный автомат со сложно структурированной памятью: часть памяти используется для идентификации шага алгоритма, остальная память используется для запоминания промежуточных данных, вычисляемых в процессе последовательного (по шагам) выполнения алгоритма. Такая модель вычислителя удобна для расчета продолжительности одного такта работы устройства.
УА инициирует последовательность шагов алгоритма в соответствии с алгоритмом выполнения операции. ОА выполняет все вычисления на отдельных шагах алгоритма под управлением УА. Кроме того, к ОА удобно отнести все вычисления предикатов, оставив УА только анализ вычисленных значений предикатов.
Конспект лекций включает разделы, относящиеся к арифметическим основам ЭВМ, основные концепции которых можно найти в учебниках[1],[2]
Каноническое описание синхронного конечного автомата можно интерпретировать как одношаговый алгоритм процедурного типа. Исполнителем этого алгоритма является ОА. На каждом шаге этого алгоритма изменяется вся память устройства, поэтому управление памятью не требуется, нет необходимости идентифицировать шаги этого алгоритма.
Проектирование ОУ включает следующие этапы:
· Изучение алгоритма выполнения операции,
· Определение необходимого состава структурных элементов ОА, таких как, регистры, сумматоры, оригинальные комбинационные схемы;
· Определение необходимых форматов структурных элементов;
· Составление граф схемы алгоритма (ГСА) выполнения операции;
· Построение управляющего автомата.
В ОА выполняются микрооперации над данными, которые поступают из памяти и хранятся в регистрах. Множество регистров образуют сверхбыструю память. Обработка данных в ОУ происходит с минимальным числом обращений к внешней памяти, а именно, обращение к внешней памяти происходит дважды за время работы автомата: первое обращение – получение данных, второе обращение – передача в память результатов обработки. Автомат такого типа называется автоматом с жесткой логикой. В отличие от микропрограммных автоматов, которые выполняют те же функции с обращением к памяти на каждом такте. Так как обращение к внешней памяти требует больших затрат времени по сравнению с обращением к регистровой памяти, автоматы с жесткой логикой имеют повышенное быстродействие. Такие автоматы являются основой RISK – процессоров.
Автомат с жесткой логикой работает в дискретном времени. Поэтому на вход УА поступает синхронизирующий сигнал, который определяет это дискретное время. В каждом такте автоматного времени УА активизирует набор микроопераций, которые выполняются в ОА. Промежуточные результаты обработки данных, а также значения предикатов, отображающих состояния отдельных элементов ОА, хранятся в регистровой памяти ОА.
| |
Микрооперация - базисное (элементарное) действие, необходимое для получения (вычисления) значения одной или более переменных. Микрооперации входят в состав микрооператоров. Микрооператор - набор взаимосвязанных микроопераций (или одна микрооперация), выполняемых одновременно и необходимых для получения одного или более значений.
| |
Микрокоманда - набор сигналов, поступающих из УА в ОА, и интерпретируемый как управляющий, т.е. необходимый для выполнения всех микроопераций данного микрооператора.
Блок схема ОУ приведена на рисунке 1. Здесь:
· Х – множество осведомительных сигналов о состоянии контролируемых элементов ОА.
· У – множество микрокоманд, вырабатываемых в УА в соответствии с ГСА.
· G – команда, инициализирующая процесс выполнения задачи.
· СС – синхронизирующий сигнал.
· КР – сигнал окончания работы ОУ.
Данные, полученные из внешней памяти, обрабатываются только в ОА. Управляющий автомат получает из ОА множество осведомительных сигналов, которые являются внешними переменными УА, и посылает в ОА управляющие сигналы. Управляющий сигнал инициирует выполнение микрокоманды, которая состоит из нескольких (возможно, одной) микроопераций.
Во многих приложениях обычная модель конечного автомата расширяется путем добавления переменных. Это дает возможность объединить наглядность представления состояний и переходов между ними с возможностями языков программирования для описания условий и действий, связанных с переходами. Подобное расширение используется, например, в языке формального описания протоколов и сервисов. Оно положено в основу стандарта UML - универсального моделирующего языка.
Арифметика ЦВМ
Формы представления чисел в ЭВМ
Для представления чисел в ЭВМ используются формы представления с фиксированной и с плавающей запятой.
Представление чисел в форме с фиксированной запятой (ФТ).
В случае целых чисел запятая фиксирована справа от младшего разряда. В случае правильных дробей запятая фиксирована слева от старшего разряда. В обоих случаях диапазон представимых чисел, определяемый как отношения максимального числа в заданной разрядной сетке к модулю минимального представимого в этой разрядной сетке числа, равен DФТ= 2n-1.
Представление чисел в форме с плавающей запятой (ПТ).
Эта форма представления называется также логарифмической. Число представляют в виде мантиссы m и порядка Π. Используется нормализованное представление чисел с плавающей запятой, при котором диапазон возможных значений мантиссы определяется неравенством p-1£ |m| < 1, и p П, где р основание системы счисления, П – целое двоичное число, разрядность которого определяет диапазон представимых чисел, m – правильная дробь, разрядность которой определяет точность вычислений. В случае k-разрядной сетки порядка (k числовых разрядов) порядок принимает значения –(2k-1) £ П £ (2k-1). Поэтому диапазон представимых чисел в форме с плавающей запятой в случае нормализованного представления равен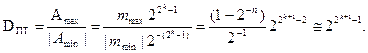 
Вычисления в форме с плавающей запятой являются принципиально не точными. Ошибка вычислений связана, с одной стороны, с погрешностью исходного представления числа, обусловленная ограниченностью разрядной сетки мантиссы, и с другой стороны, с алгоритмическими особенностями выполнения операций с плавающей запятой.
Дата: 2018-12-28, просмотров: 230.
