Перевод k-разрядного десятичного числа в двоичную систему счисления выполняется за n+1 тактов, где n – число двоичных разрядов, обеспечивающих одинаковую точность двоичного числа и исходного десятичного. Необходимое число разрядов двоичного кода n может быть определено из выражения
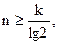 где k – число разрядов десятичного числа, определяющее его точность.
где k – число разрядов десятичного числа, определяющее его точность.
Чтобы определить алгоритм перевода числа из системы счисления с основанием q в систему счисления с основанием p, запишем числоAq в виде разложения по степеням 2:
| Aq=a1p-1+a2p-2+…+anp-n=p-1(a1+p-1(a2+…+p-1(an+0))…). | (1) |
Полученное выражение есть схема Горнера, определяющая последовательность действий при переводе.
Умножая Aq на p, получим смешанную дробь, целая часть которой будет равна первой цифре числа в системе счисления с основанием q. Далее, умножая дробную часть получившегося числа A’q на p, будем получать в целой части получающейся смешанной дроби значения очередных цифр в системе счисления с основанием р. При этом, если q>p, то цифры числа в новой системе счисления будут сразу получаться правильными. Если же p>q, то целая часть смешанной дроби, получающейся в результате умножения q-ичной правильной дроби на основание новой системы счисления будет представлять очередную цифру р-ичного числа кодовой последовательностью в q-ичной системе счисления.
Из выражения (1) следует следующий алгоритм перевода правильной дроби из кода D1 в двоичную систему счисления, представленный в табл. 1. Примем исходное число равным А10=0,13710. Число необходимых двоичных разрядов не меньше (3/lg2), т.е. больше или равно 10. Примем число двоичных разрядов равным 11 для последующего округления результата. В коде D1 наше число будет иметь вид: А10= 0001 0011 0111. Умножение числа на 2 соответствует сдвигу регистра, в котором хранится число, на один разряд влево. Исходное число, представленное в коде D1, хранится в РгА.
Для вычисления цифр двоичного кода организуется циклическая процедура. В каждом цикле вычисляется одна двоичная цифра, начиная со старшей. Очередная цифра двоичного кода, оказавшаяся после сдвига L(1)РгА слева от старшего разряда кода D1 после выполнения коррекции тетрад, записывается в младший разряд РгВ, последовательно разряд за разрядом. В каждом цикле производится декремент счетчика тактов (СТ) на 1. Работа алгоритма заканчивается, когда после очередного декремента в счетчике тактов оказывается 0. В процессе перевода РгВ сдвигается в каждом цикле на один разряд влево, освобождая место для следующего разряда. В таблице, представляющей алгоритм перевода, будем также записывать результат умножения десятичного числа на 2 в десятичной системе счисления (столбец А10), чтобы контролировать результат выполнения операций сдвига и коррекции в коде D1. Таблица также содержит столбец СТ, в котором учитывается число уже выполненных тактов. Критерием завершения операции перевода является СТ=0.
Таблица 1 Перевод правильных дробей из кода Д1 в двоичную систему счисления
| РгВ | РгА | А10 | CT | Комментарии |
| ***** ****** | 0.00001 0011 0111 | 0.137 | 11 | Загрузить [A] в РгА. СТ:=11, РгВ:=0, |
| ***** *****0 | 0.0010 0110 1110 | 0.274 | РгВ[10]:=РгА[0], РгА:=L(1)РгA, | |
| 0.0010 0111 0100 | Выполнить коррекцию в тетрадах. Сравнить полученный результат с вычисленным значением А10. | |||
| ***** ****0* | 0.0100 1110 1000 | 0.548 | 10 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 0.0101 0100 1000 | Выполнить коррекцию тетрад. | |||
| ***** ***00* | 0.1010 1001 0000 | 1.096 | 9 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 1.0000 1001 0110 | Выполнить коррекцию тетрад | |||
| ***** **001* | 0.0001 0010 1100 | 0.192 | 8 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 0.0001 1001 0010 | Выполнить коррекцию тетрад | |||
| ***** *0010* | 0.0011 0010 0100 | 0.384 | 7 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 0.0011 1000 0100 | Выполнить коррекцию тетрад | |||
| ***** 00100* | 0.0111 0000 1000 | 0.768 | 6 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 0.0111 0110 1000 | Выполнить коррекцию тетрад | |||
| ****0 01000* | 0.1110 1101 0000 | 1.536 | 5 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 1.0101 0011 0110 | Коррекция тетрад | |||
| ***00 10001* | 0.1010 0110 1100 | 1.072 | 4 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 1.0000 0111 0010 | Коррекция тетрад | |||
| **001 00011* | 0.0000 1110 0100 | 0.144 | 3 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 0.0001 0100 0100 | Коррекция тетрад | |||
| *0010 10110* | 0.0010 1000 1000 | 0.288 | 2 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| Коррекция тетрад не требуется | ||||
| 00100 01100* | 0.0101 0001 0000 | 0.576 | 1 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 0.0101 0111 0110 | Коррекция тетрад | |||
| 00101 011000 | 0.1010 1110 1100 | 1.152 | 0 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, |
| 1.0001 0101 0010 | ||||
| 00100 011000 + 1 00100 011001 | СТ=0? ДА Выход из цикла. Округление СМ:=СМ+1, | |||
| ШД:=РгB[0:10] – выдача результата в шину данных (ШД). |
Результат получается отбрасыванием младшего разряда суммы после округления.
Таким образом схема операционного автомата должна содержать тринадцатиразрядный РгА, комбинационные схемы, выполняющие коррекцию тетрад кода D1, двенадцатиразрядный РгВ, счетчик числа циклов СТ и сумматор для выполнения округления. В этом случае нет необходимости в использовании полного двоичного сумматора. Поэтому целесообразно разработать комбинационную схему, выполняющую подсуммирование 1 в младший разряд полученного двоичного числа. Следует иметь в виду, что запятая в данном случае фиксирована слева от старшего разряда.
Коррекции в коде Д1 при сдвиге влево выполняются:
1. при получении недопустимой тетрады;
2. в младшей тетраде при наличии передачи единицы из младшей тетрады в старшую,
3. коррекция в тетраде выполняется только один раз; т.е., если при коррекции возникает перенос в старшую тетраду, он не требует коррекции.
В любом случае коррекция в коде Д1 состоит в подсуммировании +6 к тетраде, требующей коррекции. При коррекции формируется символ переноса в старшую тетраду. Поэтому запись цифры из целой части дроби в коде Д1 в РгВ [10] следует производить после выполнения коррекции.
Дата: 2018-12-28, просмотров: 420.