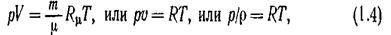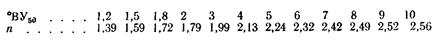Определение жидкости. Ее плотность, удельный вес и относительный вес. Сжимаемость. Температурное расширение. Закон Ньютона для жидкостного трения. Вязкость. Единицы измерения вязкости; факторы, влияющие на вязкость судовых масел и рабочих жидкостей. Парообразование. Поверхностное натяжение. Капиллярность. Понятие идеальной и реальной, ньютоновской и неньютоновской жидкостей.
Указания к теме 1.2.
Жидкостью называется непрерывная среда, обладающая свойством текучести.
Рассматриваемые в настоящем курсе жидкости можно разделить на две группы: капельные — практически несжимаемые (вода, спирт, ртуть, масла) и газообразные — легко сжимаемые (воздух и другие газы). Характерным различием этих жидкостей является также наличие у капельных жидкостей и отсутствие у газов свободной поверхности — поверхности раздела между жидкостью и газообразной средой.
Плотность представляет собой массу однородного вещества в единице объема
Размерность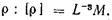 
Единицей плотности в системе
СИ является килограмм на кубический метр (кг/ма). Значения
плотности некоторых жидкостей приведены в приложениях 1 и 2.
Иногда в справочниках вместо плотности приводятся значения относительной плотности различных веществ.
Относительная плотность — безразмерная величина, представляющая собой отношение плотности рассматриваемого вещества к плотности стандартного вещества в определенных физических условиях
В качестве стандартного вещества при определении относительной плотности принимают: для твердых тел и капельных жидкостей — дистиллированную воду при температуре 277 К (4° С) и давлении 401 325 Па, имеющую плотность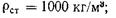 
для газов — атмосферный воздух при стандартных условиях: температуре 293 К (20° С), давлении 101 325 Па и относительной влажности 50%, имеющий плотность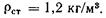 
Для непосредственного измерения плотности капельных жидкостей в технике часто используют приборы, называемые ареометрами.
Сжимаемость — свойство жидкости изменять свою плотность при изменении давления и (или) температуры.
Плотность капельных жидкостей при температуре и давлении, отличных от начальных, может быть найдена из выражения
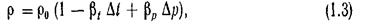
где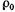 
— плотность жидкости при начальных температуре и давлении; 
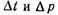— приращения температуры и давления; 
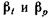— коэффициенты температурного расширения и объемного сжатия, представляющие собой относительное изменение объема жидкости при изменении температуры или давления на одну единицу:
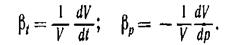
Величина, обратная ,βρ называется модулем упругости жидкости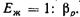 
Значения коэффициентов 
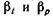весьма малы. Так, например, в интервале давлений 
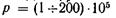Па при 
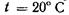средние значения 
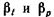составляют: для воды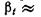 
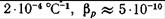Па""1; для минеральных масел, применяемых в гидроприводах,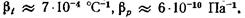 
Поэтому при решении большинства практических задач изменением плотности капельных жидкостей при изменении температуры или давления обычно пренебрегают (исключение составляют задачи о гидравлическом ударе, об устойчивости и колебании гидравлических систем и некоторые другие, где приходится учитывать сжимаемость жидкости).
В отличие от капельных жидкостей плотность газов в сильной степени зависит от температуры и давления. Рассмотрим уравнение Клапейрона — Менделеева
|
|
где р — абсолютное давление;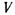 
— объем; 
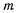— масса; 
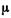— молярная масса; 
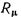— универсальная газовая постоянная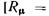 
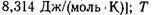— абсолютная температура; 
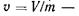удельный объем; 
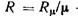— газовая постоянная [для воздуха 
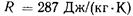, для метана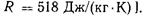 
Из этих уравнений можно установить зависимость плотности газа от температуры и давления
где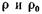 
— плотности газа соответственно при новых давлении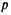 
и температуре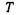 
и начальных давлении 
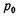и температуре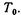 
Оценить сжимаемость жидкостей можно и другим образом. Так, в состоянии покоя характерным параметром сжимаемости жидкости является скорость распространения в ней звуковых колебаний (скорость звука)
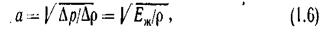
где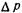 
— приращение давления; 
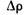— приращение плотности жидкости.
Чем больше скорость звука, тем меньше сжимаемость данной жидкости, и наоборот.
Для оценки сжимаемости движущейся жидкости пользуются обычно не абсолютным значением скорости звука, а отношением скорости потока v к скорости звука, а в данной жидкости, которое называется числом Маха,
Если скорость движения жидкости мала по сравнению со скоростью распространения в ней звука, т. е. число Маха значительно меньше единицы, то независимо от абсолютного значения скорости звука капельную жидкость (или газ) при таком движении можно считать практически несжимаемой.
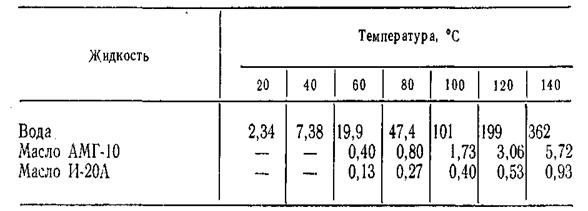
При повышении температуры или снижении давления капельной жидкости до определенных значений, когда давление станет меньше или равно давлению насыщенных паров этой жидкости при данной температуре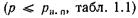 
, внутри жидкости начинают образовываться пузырьки и даже целые полости, заполненные парами данной жидкости и растворенными в ней газами, которые нарушают сплошность капельной жидкости. Таким образом, законы, установленные для сплошных сред, в этих случаях неприменимы.
Таблица 1.1
Давление (упругость) насыщенных паров некоторых жидкостей при различных температурах (рн. ш кПа)
При наличии в жидкости свободной поверхности эти пузырьки всплывают и выходят через нее, т. е. происходит кипение жидкости. Если капельная жидкость находится в замкнутом пространстве и не имеет свободной поверхности, то эти пузырьки или полости, перемещаясь в массе жидкости или вместе с ней и попадая в области с более низкой температурой или более высоким давлением, почти мгновенно (за несколько миллисекунд) смыкаются (так как пары конденсируются, а газы снова растворяются в жидкости и в образовавшиеся пустоты с большими скоростями устремляются частицы жидкости), что приводит к резкому повышению давления в этих местах, а также к местному повышению температуры. Это явление называется кавитацией.
Кавитация в трубопроводах и гидравлических машинах является крайне вредной, так как многократное местное повышение давления, сопровождающееся ударами частиц жидкости о стенки труб и проточных элементов гидромашин, приводят к их эрозии.
Капиллярность — способность капельной жидкости в трубках малого диаметра подниматься выше свободной поверхности в резервуаре, образуя вогнутый мениск (если жидкость смачивает стенки трубки), или опускаться ниже свободной поверхности, образуя выпуклый мениск (если жидкость не смачивает стенки трубки). Эта способность обусловлена поверхностным натяжением жидкости и молекулярными силами взаимодействия между жидкостями.
Рис, 1.1. Относительное движение слоев жидкости.
 |
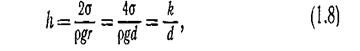Высота h поднятия или опускания жидкости в трубке может быть вычислена по формуле
где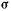 
— поверхностное натяжение; 
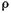— плотность жидкости;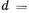 
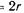— диаметр трубки; 
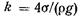— постоянная для данной жидкости.
При подстановке в формулу (1.8) d в миллиметрах значения k можно принимать равными: для воды +30 мм2, для спирта + 11 мм2, для ртути — 10 мм2 .
Вязкость — свойство жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости.
При движении реальной жидкости вследствие ее вязкости между соседними слоями жидкости, а также жидкостью и стенками русла возникают силы внутреннего трения и вызванные ими касательные напряжения, направленные в сторону, противоположную движению, что приводит к различию скоростей частиц в разных слоях потока и их деформации (сдвигу).
Если представить поток состоящим из отдельных слоев бесконечно малой толщины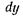 
(рис. 1.1), то скорости этих слоев будут изменяться по некоторому закону от нуля (у стенки) до максимума (в центре потока). Пусть скорости соседних слоев будут 
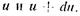В прямолинейном движении du можно рассматривать как скорость деформации, а градиент скорости 
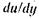как угловую скорость деформации.
Согласно гипотезе И. Ньютона, высказанной им в 1686 г,,а затем экспериментально и теоретически обоснованной в 1883 г.проф. Н. П. Петровым, сила внутреннего трения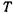 
, возникающая между двумя слоями движущейся прямолинейно жидкости, прямопропорциональна поверхности соприкасающихся слоев 
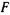, градиенту скорости 
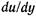, зависит от рода жидкости и температуры и не зависит от давления 1
где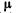 
— динамическая вязкость.
Жидкости, в которых силы внутреннего трения не подчиняются уравнению (1.9), называются аномальными или неньютоновскими. К ним относятся некоторые масла при отрицательных температурах, коллоиды, парафинистые нефтепродукты при низких температурах. Вода, воздух, спирт, ртуть, большинство масел, применяемых в гидроприводах, и другие относятся к обычным, т. е. ньютоновским жидкостям.
Разделив обе части уравнения (1.9) на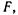 
получим касательное напряжение (напряжение силы трения)
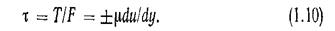
Так как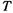 
и 
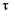всегда положительны, то в уравнениях (1.9)и (1.10) должен быть поставлен знак плюс, если 
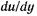положительно, и знак минус, если 
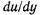отрицательно.
Из уравнения (1.10) следует, что динамическая вязкость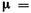 
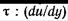численно равна касательному напряжению 
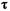при градиенте скорости 
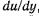, равном единице, т. е. имеет вполне определенный физический смысл и полностью характеризует вязкость жидкости.
Размерность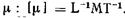 
, Единицей динамической вязкости в системе СИ является паскаль-секунда (Па*с). Широко применялась также единица системы СГС — пуаз (П = дин *с/см2); 1 П =0,1 Па-с.
При выполнении технических расчетов в гидравлике обычно пользуются кинематической вязкостью v, представляющей собой отношение динамической вязкости жидкости к ее плотности
Размерность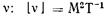 
Единицей кинематической вязкости в системе СИ является метр в квадрате на секунду (м'2/с)2.
Широко применялась также единица системы СГС — сантиметр в квадрате на секунду, называвшаяся стокс (сма/с = Ст), а также ее производная — сантистокс (сСт); 1 ма/с = 104 Ст = 10е сСт. В соответствии с СТ СЭВ 1052—78 такие единицы вязкости, как пуаз, стокс, сантистокс в настоящее время не применяются.
Для определения вязкости жидкостей используют приборы, называемые вискозиметрами. Для измерения вязкости жидкостей более вязких, чем вода (масел, нефтепродуктов) применяют обычно вискозиметр (рис. 1.2), состоящий из двух сосудов, пространство между которыми заполняется водой для поддержания требуемой температуры. К сферическому дну внутреннего сосуда прикреплена трубочка с внутренним диаметром .около 3 мм, отверстие в которой нормально закрыто клапаном.
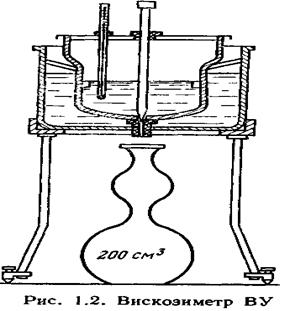
Во внутренний сосуд до определенного уровня наливается испытуемая жидкость и с помощью нагревательного устройства температура ее доводится до требуемого значения t', фиксируемого термометром, после чего клапан открывается и с помощью секундомера измеряется время истечения 200 см3 этой жидкости. Аналогичный опыт производят с дистиллированной водой при t = 20° С. Отношение измеренных времен истечения испытуемой жидкости Ти,ж и дистиллированной воды Тд,п составляет число градусов условной вязкости (или градусов Энглера):
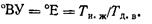
Для перевода градусов условной вязкости в единицы системы СИ (м2/с) пользуются эмпирической формулой Уббелоде
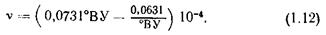
Вязкость зависит от рода жидкости, ее температуры и давления. Значения вязкости некоторых жидкостей в различных единицах приведены в приложениях 1 и 2.
С увеличением температуры вязкость капельных жидкостей уменьшается, а газообразных — увеличивается. Зависимость вязкости от температуры для разных жидкостей различна и выразить ее аналитически общим уравнением не представляется возможным.
При выполнении расчетов можно воспользоваться следующими зависимостями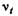 
(м8/с): для воздуха
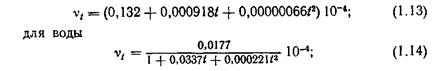
Для минеральных масел, применяемых в гидроприводах в интервале температур 30—150° С и при вязкости до 10°
|
|
где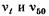 
— кинематическая вязкость соответственно при данной температуре и при 50° С; t — температура, °С; п — показатель степени, значение которого в зависимости от °ВУ составляет
|
|
Характер изменения вязкости жидкостей при изменении давления различен и зависит от начальной вязкости и температуры. Для большинства капельных жидкостей с повышением давления вязкость несколько увеличивается.
Вязкость минеральных масел в пределах давлений 0—50 МПа изменяется практически линейно и может быть вычислена по формуле
где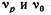 
— кинематическая вязкость соответственно при давлении р и атмосферном давлении; 
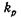— опытный коэффициент (при расчетах систем гидроприводов в пределах указанных давлений принимается равным 0,03); 
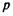— давление, при котором определяется вязкость, МПа.
Вопросы для самопроверки.
1. В чем состоит отличие жидкостей от твердых тел и газов?
2. Какова взаимосвязь между плотностью и удельным весом?
3. Как изменяется плотность жидкости при увеличении давления
и температуры?
4. Какова связь между коэффициентом объемного сжатия и объемным модулем упругости?
5. Что представляет собой коэффициент температурного расширения?
6. Что называется вязкостью? В чем состоит закон жидкостного
трения Ньютона?
7. Какова связь между динамическим и кинематическим коэффициентами вязкости?
8. Чем отличается идеальная жидкость от реальной?
9. Что называется давлением насыщенных паров жидкости и от чего оно зависит?
10. Что такое поверхностное натяжение и от чего оно зависит?
Литература: 1, 3.
Задачи.
1. Стальной барабан подвергается гидравлическому испытанию созданием избыточного давления Р. Определить, какое количество воды дополнительно к первоначальному объему при атмосферном давлении необходимо подать насосом в барабан, если его геометрическая емкость равна V . Деформацией барабана пренебречь, модуль упругости воды принять равным 1960 МПа
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Р, МПа | 1,66 | 1,60 | 1,76 | 1,70 | 1,86 | 1,80 | 1,96 | 1,90 | 2,24 | 2,36 |
| V, м3 | 8 | 9 | 10 | 11 | 12 | 8 | 9 | 10 | 11 | 12 |
2. Для испытания на герметичность резервуара произведена его отпрессовка, т.е. наполнен под давлением P 1 жидкостью, имеющей модуль упругости E . За время t давление в резервуаре вследствие утечек жидкости через швы понизилось до Р2. Сколько за это время из резервуара вытекло жидкости, если он имеет форму цилиндра диаметром d= 780 мм и высотой h=1,5 м? Деформацией стенок резервуара пренебречь.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Е, МПа | 2000 | 1400 | 1300 | 1350 | 1400 | 2000 | 1350 | 2000 | 1300 | 1400 |
| Р1 атм | 25 | 40 | 50 | 30 | 35 | 45 | 28 | 32 | 37 | 48 |
| Р2 атм | 20 | 35 | 42 | 28 | 33 | 42 | 25 | 30 | 33 | 44 |
| t, ч | 24 | 10 | 16 | 2 | 6 | 8 | 12 | 14 | 18 | 20 |
3. Трубопровод диаметром d = 0,5 м и длиной l наполнен водой, находящейся в состоянии покоя при давлении Р=4 атм и температуре воды t1 . Определить, пренебрегая деформациями к расширением стенок труб, на сколько изменится давление в трубопроводе при нагревании воды в нем до 15°С, полагал коэффициент температурного расширения воды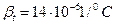 
, а коэффициент объемного сжатия 
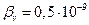м2/Н.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, м | 500 | 1000 | 900 | 800 | 700 | 600 | 1000 | 900 | 800 | 700 |
| t1, 0С | 4 | 5 | 6 | 7 | 8 | 5 | 6 | 7 | 8 | 5 |
Примеры решения задач
Задача 1.
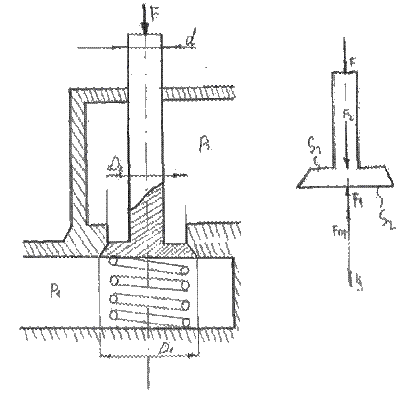
Определить силу F, которую нужно приложить к хвостовику клапана распределительного устройство объемного гидропривода для отрыва его от седла, если усилие пружина Fпр=300 Н, давление в полости отвода жидкости к клапану Р1=0,6 МПа, в положении отвода жидкости Р2=0,4 МПа, D1=50мм, D2=40мм,
d=10 мм. Силой трения покоя и весом клапана пренебречь.
Решение.
Рассмотрим систему сил, действующих на клапан распределительного устройства: 1. Сила давления в полости подвода жидкости Р1: F1=S1.P1, где S1 – площадь нижнего основания клапана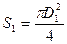 
, тогда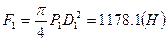 
2. Сила давления в полости отвода жидкости Р2: F2=S2.P2, где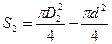 
, тогда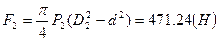 
3. Сила Fпр пружины, действующая по нормали к площадке S1
4. Сила F, действующая на верхнее основание клапана, так как система изолирована, то согласно 3-му закону Ньютона составляем уравнение равновесия относительно оси y: F+F2-F1-Fпр=0 =>F=Fпр+F1-F2=1000,86 (Н)
Задача 2.
В гидрозамке проходное сечение открывается при подаче в полость А управляющего потока жидкости с давлением Ру. Определить, при каком минимальном значении Ру толкатель поршня 1 сможет открыть шариковый клапан, если известны: 2 F=50Н, D=25 мм, d=15мм, Р1=0,5мПа.
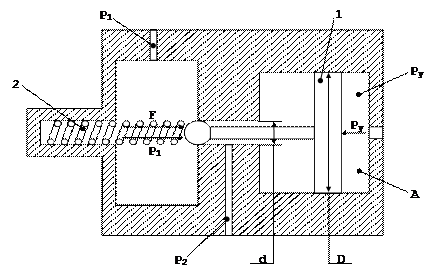
Решение.
- Рv+F+Р1=0, уравнение равновесия на ось ох, из этого уравнения определяем Рv: Рv=F+Р1, из этого уравнения определяем Р1: Рv=π.d2=353Н; определяем силу Рррррррр v: Рv=Р1+F=403Н; определяем давление Р1: Рv=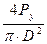 
= 0,8мПа.
Задача 3.
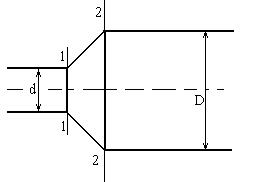
Пренебрегая потерями напора, определить степень расширение диффузора n=(D/d)2 при котором давление в сечении 22 возрастает в 2 раза по сравнению с давлением 11. Расчет произвести при следующих данных: расход жидкости
Q=1,5 л/с, d=20 мм, давление в сечений 11 Р1=1 кПа, плотность жидкости
ρ=1000 кг/м3.
Решение.
Из уравнения расхода жидкости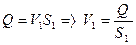 
, составим уравнение Бернулли для сечений 11 и 22 
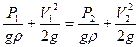отсюда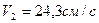 
Из уравнения постоянства расхода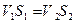 
, находим D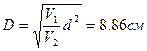 
Степень расширение диффузора n=(D/d)2=4,9
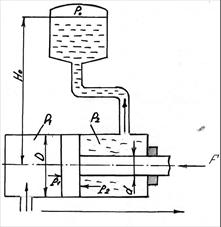
Задача 4.
Определить давление Р1 жидкости, чтобы преодолеть усилие, направленное вдоль штока F= 1 кН. Диаметр цилиндра D=50 мм, штока d=25 мм, давление в бачке Р0=5кПа, высота Н0=5 м. Силу трения не учитывать. Плотность жидкости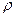 
=1000 кг/м3
Решение
1. Составляем уравнение равновесия :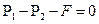 
, отсюда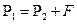 
2. Находим давление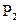 
: 
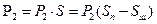
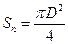, где D=0,05 м
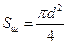, где d=0,025 м
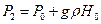, тогда
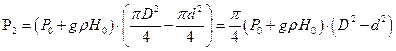
3. Находим давление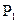 
: 
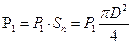
4. Давление жидкости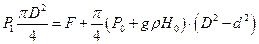 
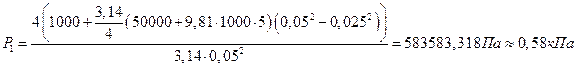
Раздел 2.
Дата: 2018-12-28, просмотров: 583.
