Для анализа сложных линейных цепей иногда применяется метод эквивалентного генератора, основанный на теореме об активном двухполюснике, называемой также теоремой Гельмгольца-Тевенена, (H.Helmholtz, L.Thévenin), позволяющий определить ток в одной ветви сложной линейной схемы, не находя токи в остальных ветвях.

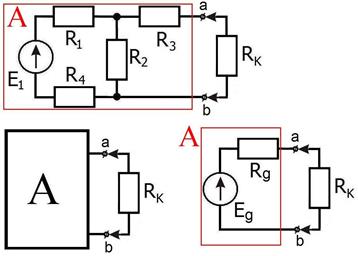
Рис. 2.6.

Выделенную часть схемы (А) заменяем двухполюсником с той же буквой.

Любую линейную схему внутри двухполюсника А можно заменить простой эквивалентной схемой с генератором напряжения E _g  и внутренним сопротивлением R _g .

Пользуясь этим методом, любой сколь угодно сложный активный двухполюсник можно представить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах двухполюсника. Внутреннее сопротивление равно входному сопротивлению пассивного двухполюсника со стороны тех же зажимов.

При определении входного сопротивления все источники должны быть заменены своими внутренними сопротивлениями, источники ЭДС закорачиваются, а источники тока размыкаются.

Можно также найти внутреннее сопротивление, поделив эквивалентную ЭДС на ток короткого замыкания.

Аналогично находятся параметры активного двухполюсника и при синусоидальном токе; только в этом случае необходимо заменить сопротивления  комплексными импедансами, а
E _g – комплексным Ẽ _g .

Для примера сосчитаем параметры эквивалентного генератора для схемы на рис. 2.6 с номиналами деталей: R₁ = R₄ = 1кОм, R₂ = R₃ = 2кОм, E₁ = 10 В.

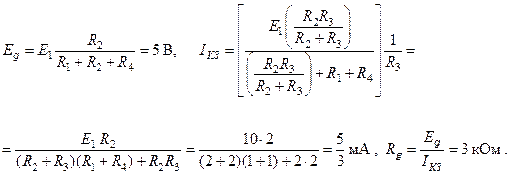
                         В скобках – напряжение на R₂  и R₃ при коротком замыкании .

Итак, схему можно заменить эквивалентным генератором с напряжением Е _g = 5 В и с внутренним сопротивлением R_g = 3 кОм.

Анализ линейных систем

Стационарная система – это система, в которой сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала. В общем случае анализ линейной стационарной системы сводится к решению системы линейных дифференциальных (или интегро-дифференциальных) уравнений с постоянными коэффициентами. Такие системы называются линейными и стационарными. Для получения этих уравнений используются известные правила Кирхгофа. Вот они.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю. Узлом называется точка, в которой сходится более чем два проводника. Это правило вытекает из закона сохранения заряда. Число уравнений, составленных по первому правилу Кирхгофа, должно быть на одно меньше, чем число узлов в исследуемой цепи. Этим обеспечивается линейная независимость получаемых уравнений.

Второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре. При составлении уравнений согласно второму правилу Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода.

Задача простая, но громоздкая. Например, для схемы на рис. 2.7 получаются следующие уравнения:

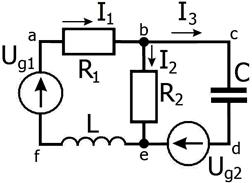
Рис. 2.7.

Схема для демонстрации правил Кирхгофа. На изображениях электрических цепей (на схемах) провода заменяют отрезками прямых. Считают, что провода на схеме имеют нулевое сопротивление.

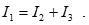
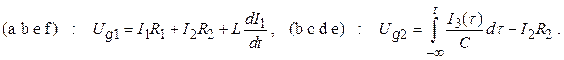
Контур

Решение системы линейных интегро-дифференциальных уравнений обычно громоздко. Чтобы избежать громоздкости применяют различные методы, среди которых на первом месте – метод комплексных амплитуд (для гармонических сигналов). Этот метод позволяет заменить интегро-дифференциальные уравнения на алгебраические.

Для линейных стационарных систем справедлив принцип суперпозиции:

если в цепи есть несколько источников тока или напряжения, то можно рассчитать отклик системы на каждый источник отдельно. Тогда отклик системы в целом будет просто равен сумме отдельно рассчитанных откликов.

Каждый источник не влияет на другие, а работает независимо.

Хотелось бы подчеркнуть, что принцип суперпозиции справедлив только в линейных системах.

Метод комплексных амплитуд

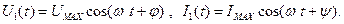Пусть в линейной цепи действуют гармонические источники напряжения  U  или тока I
на частоте ω .

Тогда установившиеся токи и напряжения будут иметь ту же частоту, но разные фазы. Для расчёта амплитуд и фаз установившихся колебаний применяется символический метод (метод комплексных амплитуд, Ch. P. Steinmetz).

Напомним некоторые формулы из теории комплексных чисел:

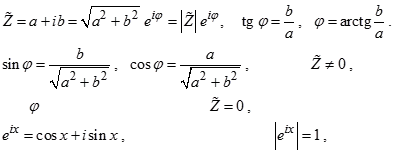
                                                            если

        не определено, если

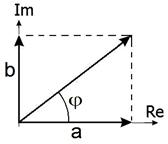
                           (формула Эйлера),                                                                  Рис. 2.8.

Значок ~ над числом показывает, что число (или функция) – комплексные.

Метод комплексных амплитуд или символический метод позволяет представить любую колеблющуюся гармонически величину в виде квази-вектора, вращающегося с круговой частотой ω . Тогда любую функцию, зависящую от времени по гармоническому закону, можно представить как действительную часть комплексной экспоненты:

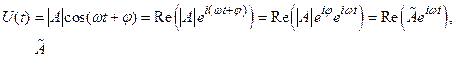
                                                                                                                                           (2.9)

где      – комплексная амплитуда, а φ - фаза.

Такие квази-векторы удобно применять для изображения гармонических переменных токов, однако они изображают только амплитуды (своей длиной) и проекции на оси. Направления в пространстве, (в отличие от настоящих векторов), они не указывают.

При такой записи операции дифференцирования и интегрирования (в смысле нахождения первообразной) сведутся к операциям умножения и деления:

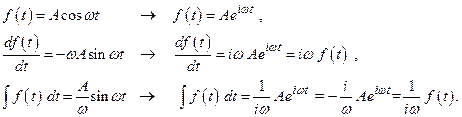
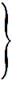
                                                                                                                                            (2.10)

Векторная диаграмма рис. 2.8 – мгновенная картина. При  ω t = 0, 2 π и т.д. e ^iωt = 1. При такой временной зависимости картина будет вращатьсяпротив часовой стрелки с угловой скоростью ω. Это можно представить, если написать, что e ^iωt = ,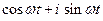
и проследить, как будет меняться синус и косинус с увеличением времени.

Конечно, если зависимость от времени будет  e ^{– iωt} , то вращение будет по часовой стрелке.

Это можно увидеть воочию при помощи программки на Матлабе.

(Кстати, написанное мелким шрифтом можно пропускать без ущерба для понимания).

clc; %чистит окно команд

FigureColor=[1,1,1]; hFigure=gcf; set(hFigure, 'Color', FigureColor) %удаляют рамку графика

title('exp(+ i \omega t)','FontSize', 28); %заголовок, omega – круговая частота.

tic;pause(2);toc; %время для прочтения заголовка

for t = 0:0.027:2*pi; axis([-1 1 -1 1]) %границы области графика

x=-sin(t); y=cos(t);    h = plot(x,y,'k.'); hold on; pause(0.01)

end; pause(2)

clf; %чистит графическое окно

title({' '; 'exp(– i \omega t)'}, 'FontSize', 28); %заголовок, omega – круговая частота.

tic;pause(2);toc; %время для прочтения заголовка

for t = 0:0.028:2*pi; axis([-1 1 -1 1]) %границы области графика

x=sin(t); y=cos(t); h = plot(x,y,'ro'); hold on; pause(0.01)

end; pause(1); clf;

Если напряжения и токи в цепи зависят от времени не гармонически, то можно разложить их по гармоническим составляющим в ряд или интеграл Фурье:

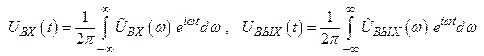
                                                                                                               .                              (2.11)

К этому методу мы ещё вернёмся (см. (3.20), (3.21)).