Рассмотрим в качестве примера разложение в тригонометрический ряд Фурье в форме (3.1) периодической функции, изображённой на рис. 3.8. Это прямоугольные импульсы.
Рис. 3.8.
График периодической функции.
Синус нарисован для иллюстрации
того простого факта, что интеграл
произведения этих двух
функций равен нулю. Здесь τ = T/2.
Кстати, здесь постоянная составляющая a0/2 = U0/2.
Мы провели оси так, чтобы функция стала чётной. Поэтому все коэффициенты bn будут равны нулю. Это видно на рис. 3.8. Интеграл от произведения чётной функции на синус любой частоты равен нулю.
Постоянной составляющей соответствует коэффициент a 0 /2.
(3.15)
Заметьте, что постоянная составляющая в ряде Фурье равна а0 /2.
Остальные спектральные составляющие будут располагаться на оси частот эквидистантно, и их амплитуды и фазы будут определяться функцией вида (sin x)/x.
(3.16)
Первый нуль огибающей будет при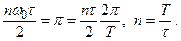 
Эта гармоника "пропадает". Для меандра τ = T/2.
Функции и называются гармониками. (3.17)
Часто гармониками называют и их амплитуды cn .
Рис. 3.9.
Такую функцию в радиотехнике называют "меандр", по имени древнегреческой реки. Длительность импульса равна половине периода τ/ T = 1/2. Нули огибающей совпадают с чётными гармониками. Остаются только нечётные.
Амплитуда первой гармоники 2 U0 / π . Помните, что постоянная составляющая – это a0 /2.
График гармоник Фурье для периодических прямоугольных импульсов с отношением τ/ T = 1/4 приведён на рис. 3.10.
Рис. 3.10.
Гармоники спектра Фурье прямоугольных импульсов.
Здесь и далее постоянная составляющая указана условно, так как нуль напряжения фиксирован только на графике рис. 3.8.
Принято изображать гармоники не точками на графике, а линиями и называть такой спектр линейчатым. Часто на графиках изображают модуль огибающей функции.
На рис. 3.10 первый нуль огибающей спектра для импульсов с длительностью τ = T/4 приходится на четвёртую гармонику. Действительно, аргумент синуса равен π при n = T/ τ . Чем короче будет импульс, тем больше гармоник будет помещаться в низкочастотной части спектра до первого нуля огибающей. В этой области спектра, в гармониках с номерами n < N* ~ T/ τ лежит бо́льшая часть энергии импульса. При N* >> 1 , более 90% энергии спектра приходится на гармоники с номерами n < N* .
Можно переформулировать это на частотном языке: более 90% энергии спектра лежит на частотах менее 1/ τ Гц, а номеру N* соответствует круговая частота ω* ~ N* ω 0 = 2 π / τ .
Ещё раз сравним спектры прямоугольных импульсов с одинаковой длительностью τ , но с разными периодами Т .
Рис. 3.11A.
.
Тут пропадают гармоники, кратные шести.
Рис. 3.11Б.
Комплексный спектр, аналогичный изображённому на рис. 3.11А.
|С̃̃n|
an 
Рис. 3.12.
.
Редкие импульсы. Огибающая всё та же, а гармоники располагаются очень часто. Спектр постепенно от линейчатого приближается к сплошному.
Кстати, функция sin(x)/x ≡ sinc(x) и называется "Sinus Cardinalis", то есть "Основной или главный синус".
Если собирать прямоугольные импульсы из конечного числа гармоник становится ясно, что гармоники более высоких номеров (высокочастотные) делают передние и задние фронты импульсов всё круче и круче, как это видно на рис. 3.13.
Рис. 3.13А. Нижние импульсы собраны из первых 10 гармоник, верхние – из 50. Из-за эффекта Гиббса выброс на 9% выше вершины.
На фронтах импульсов всегда видны характерные выбросы, соответствующие последнему номеру гармоники. Это так называемое явление или эффект Гиббса, открытый за пятьдесят лет до Гиббса Г.Уилбрагамом (H.Wilbraham).
Рис. 3.13Б.
Фронты импульсов рис. 3.13А, собранных из 50 и 500 гармоник.
1. Амплитуда выбросов одинакова (±9%).
2. Чем больше гармоник – тем круче фронт.
Уилбрагам обнаружил, что в месте разрыва функции ряд Фурье, состоящий из конечного числа членов, даёт выброс на месте разрыва (на фронте) с амплитудой ±9% от амплитуды импульса. Этот эффект показан на рис. 3.13Б, где представлен вид фронта прямоугольных импульсов (рис. 3.13А), вычисленный суммированием 50 и 500 гармоник спектра.
Однако на экранах осциллографов при наблюдении импульсных сигналов таких выбросов обычно нет, хотя усилители осциллографов имеют конечную полосу пропускания. Чтобы разобраться с этой загадкой мы пропустили гармоники через фильтр, ослабляющий высокочастотные гармоники (на компьютере, конечно). ЧХ фильтра приведена на рис. 3.14.
Рис. 3.14.
Коэффициент передачи фильтра, применённого к импульсу рис. 3.13А, состоящему из пятидесяти гармоник.
Рис. 3.15. Прямоугольный импульс, собранный из 50 гармоник и тот же импульс, пропущенный через фильтр.
Видно, что выбросы на фронтах импульсов, пропущенных через фильтр, который ослабляет тридцатую гармонику вдвое, а пятидесятую в восемь раз, меньше по амплитуде.
Рассмотрим ещё один пример: разложение в спектр Фурье периодических пилообразных импульсов (рис. 3.16).
Рис. 3.16. Периодические пилообразные импульсы (пила).
Напряжение такой формы на промежутке [0, Т] можно описать функцией,
где Т – период функции. При t = 0 U = U0 , при t = T/2 U = 0.
На графике видно, что функция нечётная, следовательно все а n = 0.
Справка:
Так как ω0 = 2π/ T , то третий член равен нулю, первый и пятый уничтожаются.
Остаётся: (3.18)
| Рис. 3.17. На этом рисунке показаны первое и второе слагаемые суммы в формуле (3.18) и их сумма. Обычно говорят, что это сумма первой и второй гармоник. Эта сумма лишь отдалённо напоминает исходную пилу. Однако сумма содержит 76% энергии пилы. | Рис. 3.18. На этом рисунке добавлена ещё и третья гармоника. Фронт стал круче. |
Рис. 3.19.
На этом рисунке приведены суммы трёх и десяти гармоник. Фронт стал ещё круче.
Длительность фронта определяется длительностью четверти периода высшей гармоники.
Рис. 3.20.
И, наконец, приведены суммы десяти гармоник и двух тысяч гармоник. Этих гармоник уже хватило для того, чтобы на рисунке такого формата импульс мало отличался от того, который мы раскладывали в ряд Фурье. Чем больше гармоник мы учитываем, тем круче становится фронт, и тем точнее форма импульса совпадает с исходной.
50 2
Рис. 3.21.
Суммы двух и пятидесяти гармоник для треугольного импульса. Импульсы немного сдвинуты для удобства сравнения.
Вы уже заметили, что амплитуды гармоник прямоугольного и пилообразного импульсов убывают как 1/n. Это сравнительно медленное убывание – следствие наличия разрыва функции. Если взять более гладкую функцию, например периодические треугольные импульсы, то амплитуды гармоник будут убывать быстрее, как 1/n 2 (см. (3.19)).
. (3.19)
На рис. 3.21 показаны результаты сложения двух и пятидесяти гармоник треугольных импульсов. Если сравнить результат с суммой двух гармоник для пилообразных импульсов (см. рис. 3.17), то станет ясно, что для аппроксимации более гладкого сигнала нужно меньше гармоник.
Равенство Парсеваля
Рассмотрим для примера периодический ток I( t), протекающий по сопротивлению R. Величина средней по периоду мощности на сопротивлении будет:
Разложим I( t) в ряд Фурье:
Тогда
После возведения в квадрат получится сумма интегралов вида:
Первые три типа интегралов от знакопеременных функций будут равны нулю.
Интегралы четвёртого и пятого вида при k ≠ m будут интегралами от знакопеременных функций и будут равны нулю. При k = m они будут равны:
Если обозначить постоянную составляющую тока , а амплитуду n-ной гармоники
то выражение для мощности можно будет переписать в виде:
Видно, что мощность периодического переменного тока равна
сумме мощностей его гармонических составляющих – членов ряда Фурье.
В учебниках математики равенство:
называют равенством Парсеваля.
Равенство Парсеваля – это аналог теоремы Пифагора.
Оценим мощность первых гармоник тока в виде меандра (см. рис. 3.9).
Средняя мощность тока в виде меандра равна , так как ток течёт только половину периода.
Мощность первой гармоники от N0 .
Второй гармоники нет.
Мощность третьей гармоники от N0 .
Таким образом, в первых двух гармониках меандра содержится 45% мощности. Эти расчёты могут быть полезными при оценке энергии, которую можно передать при помощи радиоволн или по проводам.
Пример спектра музыкального сигнала
В действительности сигналы редко бывают такими простыми. Вот, для примера, фрагмент записи звука рояля. Основной звук – нота до диез второй октавы из седьмого вальса Шопена. Частота такого звука – 554.36 Гц. Нижняя шкала – время в секундах.
Рис. 3.22А.
Часть записи седьмого вальса Шопена.
Основной звук – нота до диез второй октавы. Слышен и слабый звук ноты ре первой октавы.
Рис. 3.22Б.
Спектр этой записи. Логарифмическая шкала. Самый высокий пик соответствует частоте 554 Гц. Левее пик ноты ре первой октавы. Правее – гармоники 554·2 = 1108 Гц и 554·3 = 1662 Гц.
Анализатор из программы Cool Edit.
Преобразование Фурье
Строго говоря, периодических процессов не бывает. Каждый процесс когда-то начался и наверняка закончится. На графике рис. 3.12 видно, что если импульсы повторяются редко, то до первого нуля огибающей помещается много гармоник. Если период увеличивать, то гармоники нашего линейчатого спектра сольются в сплошной. А огибающая останется прежней. Если представить, что сигнал один и ни слева, ни справа от него ничего не видно, то мы можем приближённо считать этот сигнал одиночным, непериодическим. Для анализа непериодических сигналов применяется преобразование Фурье.
Из курса математики известно, что любую достаточно хорошую функцию F( t) можно разложить в интеграл Фурье:
(3.20)
(3.21)
Обычно саму функцию времени F( t) и её Фурье-образ F( ω) обозначают одной буквой. Это не должно привести к недоразумениям, так как аргумент ( t или ω) указывает на то, что имеется в виду.
Заметим, что иногда коэффициент 1/2π в формулах преобразования Фурье распределяют иначе, например, так:
Встречаются и другие варианты. Мы будем пользоваться определением (3.20, 3.21).
В качестве продолжения примера из предыдущего раздела вычислим преобразование Фурье (или спектр Фурье) одиночного прямоугольного импульса амплитуды U0 и длительности τ.
(3.22)
Осталась одна огибающая, а гармоники слились в сплошной спектр.
Приведём основные свойства интегралов Фурье:
F1 ( t) + F2 ( t) + F3 ( t) ↔ F1 ( ω) + F2 ( ω) + F3 ( ω) , (3.23)
α F (t) ↔ α F ( ω ) , α = const. (3.24)
(3.25)
(3.26)
(3.27)
(3.28)
!!!!! (3.29)
(3.30)
Приведём доказательства некоторых свойств интегралов Фурье, приведённых выше.
Дата: 2018-12-28, просмотров: 274.
