2.1 Построение плана механизма в 8-ми положениях (через 45^°)

Исходные данные: ℓ_ОА = 0,20 м = 200 мм;  ℓ_АВ = 0,60 м = 600 мм; ℓ_ВС = 0,40 м = 400 мм; ℓ_ОС = 0,80 м = 800 мм.

Из условия размещения плана на листе выбирается масштабный коэффициент длины звеньев

К_ℓ =  = ,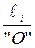

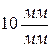где ℓ_ί – длина звена в мм;

     "O"– длина отрезка, изображающего длину звена на плане.

С учетом К_ℓ = 10 мм/мм длины звеньев на плане:

ОА = 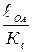 =  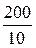= 20 мм; АВ =  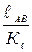=  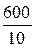= 60 мм;

ВС = 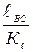 =  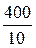= 40 мм; ОС =  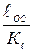=  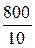= 80 мм.

В выбранном масштабе вычерчиваются планы механизма. По горизонтали откладывается отрезок ОС = 80 мм и обозначается неподвижное звено точками О и С.

Из точки "O" проводится окружность радиусом ОА = 20 мм – траектория движения точки А кривошипа, которая делится на 6-8 равных частей (через 45° или 60°). Точки А окружности нумеруются А₁, А₂, А₃, А₄, А₅,А₆, А₇ и А₈ в направлении вращения от начального.

Из точки С проводится   дуга окружности радиусом коромысла СВ = 40 мм. Из каждой точки положения кривошипа А₁ … А₈ радиусом АВ = 60 мм (длина шатуна) проводятся дуги окружности до пересечения с дугой окружности СВ = 40 мм. В местах пересечения отмечаются соответствующие точки В₁, В₂ и т.д., которые соединяются отрезками А₁В₁, А₂В₂ и т.д. На середине каждого отрезка А₁В₁, А₂В₂ и т.д. отмечается точка положения центра масс шатуна S₁… S₈. Соединение этих точек позволяет получить фигуру в виде овала, которая соответствует траектории движения центра масс шатуна S₂.

В результате построены планы механизма в 8-ми положениях в зависимости от угла поворота кривошипа, которые представлены на рис. 3.

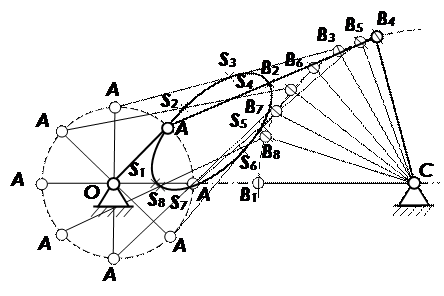Рис. 3 Планы механизма в 8-ми положениях

2.2 Траектории движения центра масс шатуна (точки S₂) и

характеристика траекторий движения точек А, В, S₂

По планам механизма (рис. 3) получена траектория движения центра масс шатуна (точки S₂), которая представляет фигуру типа «овал». Траектория движения точки "А"– окружность, точки "В"- дуга окружности.

2.3 Кинематическая схема механизма в заданном положении

Исходные данные: φ₁ = 135°; ℓ_ОА = 0,20 м; ℓ_АВ = 0,60 м; ℓ_ВC = 0,40 м; ℓ_OС = 0,80 м;

частота вращения кривошипа n₁ = 760 об/мин или угловая скорость вращения кривошипа:

ω₁ = 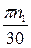 =  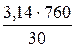= 80 рад/с.

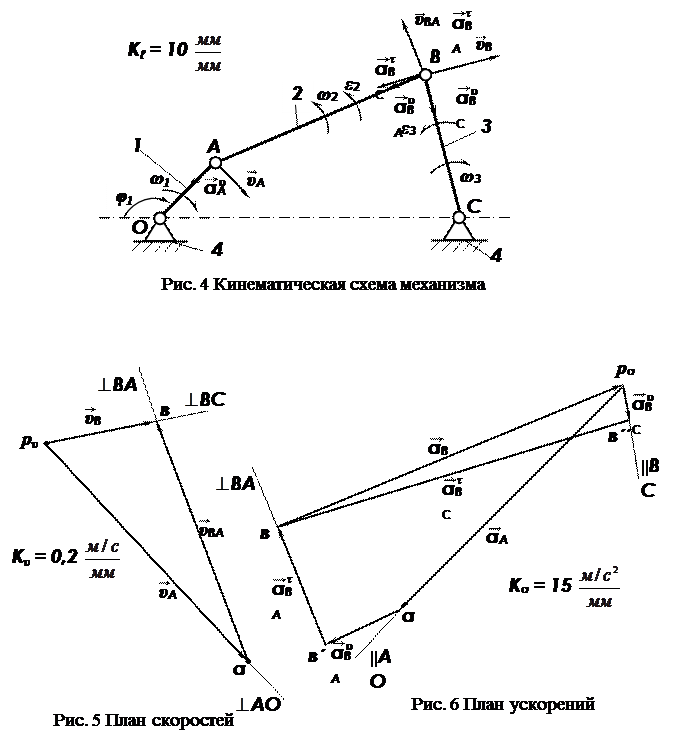
В принятом масштабе К_ℓ = 10 мм/мм на отдельном листе изображена кинематическая схема механизма при φ₁ = 135° (рис. 4) и под ней планы скоростей (рис. 5) и ускорений (рис. 6).

2.4 Определение линейной скорости точек А, В; угловой скорости

 шатуна, коромысла и их направления

Линейные скорости характерных точек механизма А и В и их направление определяются из плана скоростей, который строится в масштабе

К_υ = ,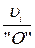

где υ_ί – значение линейной скорости ί-ой точки;

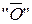 - длина отрезка в мм, изображающая скорость ί-ой точки на плане.

Скорость точки А: υ_А = ω₁ℓ_ОА = 80 · 0,2 = 16 м/с.

Из условия размещения плана скоростей совместно с кинематической схемой принимаем масштабный коэффициент скорости К_υ = 0,2 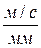 и обозначаем полюс плана скоростей – точка р_υ (рис. 6).

Вектор 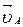 приложен в точке А перпендикулярно звену 1 и направлен в сторону его вращения. На плане скорость  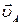изображается отрезком

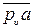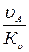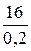 =  =  = 80 мм, отложенным из полюса плана р_υ (рис. 5).

Скорости неподвижных точек О и С равны нулю, и точки О и С на плане совпадают с полюсом р_υ.

Для определения скорости точки В используем векторные уравнения:

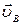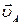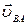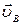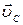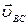=  +  и  =  +                                 (1)

где 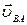 - относительная скорость точки В при вращении вокруг точки А, направлена перпендикулярно звену ВА;

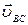- относительная скорость точки В при вращении вокруг точки С, направлена перпендикулярно звену ВС.

Так как 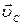 = 0, то  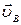=  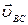приложена в точке В и направлена перпендикулярно ВС.

С учетом этого

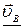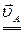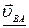 =  + .                                  (2)

⊥ВС⊥АО⊥ВА.

В уравнении (2) подчеркнуто число известных параметров. Векторное уравнение (2) с двумя неизвестными величинам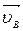и  и 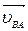 решается путем построения плана скоростей.

Из произвольно выбранного полюса р_υ (рис. 5) откладываем отрезок 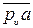 = 80 мм перпендикулярно звену АО, в направлении вращения. Из полюса ρ_υ проводится направление вектора  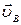перпендикулярно ВС, а из точки "а" (конца вектора 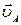) проводится направление вектора  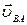перпендикулярно ВА до пересечения с направлением вектора 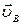. Пересечение направлений дает точку "в" – конец векторов  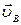и 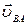. Измерив по плану отрезк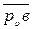и  и 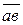 в мм получим:

скорость точки В υ_В = К_υ · 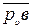 = 0,2 · 30 = 6,0 м/с;

относительная скорость υ_ВА = К_υ · 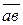 = 0,2 · 70 = 14 м/с.

Направления скоростей указаны на плане и перенесены на схему рис.4.

Величины угловых скоростей звеньев определяем по формулам:

ω₂ = υ_ВА/ℓ_АВ = 14/0,6 = 23,3 рад/с;

ω₃ = υ_В/ℓ_ВС = υ_В/ℓ_О2В = 6,0/0,40 = 15 рад/с.

Для определения направлений угловых скоростей переносим векторы относительных линейных скоростей в соответствующие точки плана механизма (рис. 4) и укажем их направление.

2.5 Определение линейного ускорения точек А и В, углового

ускорения звеньев и их направления

Так как звено 1 (ОА) вращается равномерно (ω₁ = 80 рад/с = const), то точка А имеет только нормальное ускорение

а_А = 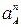 =  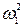· ℓ_О1А = 80²·0,2 = 1280 м/с².

Линейные ускорения характерных точек механизмов А и В определяются из плана ускорений, который строится в масштабе из полюса плана р_а (рис. 6).

К_а = ,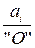

где а_ί – значение линейного ускорения, м/с²;

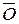" " - длина отрезка в мм, изображающая ускорение на плане.

Принимаем масштабный коэффициент ускорения К_а = 15 .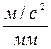

Вектор 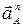 приложен в точке А и направлен вдоль звена АО к центру вращения в точке О. На плане ускорений ускорение  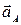изображается отрезком  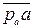=  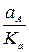=  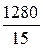= 85 мм, отложенным из полюса плана р_а (рис. 6).

План ускорений строится по аналогии с планом скоростей, используя векторные уравнения, считая, что абсолютное ускорение слагается из нормального и касательного.

Уравнения для определения ускорений , , :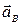

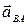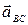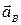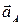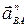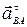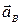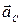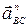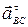 =  +  +  и  =  +  +                      (3)

Так как а_С = 0, то

=  +  =  +  +

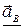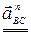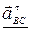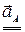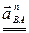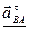
║ВС⊥ВС ║ АО║ ВА ⊥В А,                (4)

где нормальные ускорения равны:

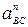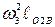 =  = 15² · 0,40 = 90 м/с²;

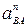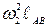 =  = 23,3² · 0,6 = 326 м/с².

В масштабе К_а = 15 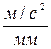 отрезки, изображающие нормальные составляющие ускорений, на плане представлены:

ускорение 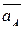 отрезко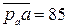м  мм;

ускорение 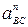 отрезком  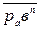= 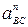/К_а = 90/15 = 6 мм;

ускорение 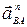 отрезком  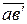= 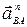/К_а = 326/15= 22 мм.

Направление векторов нормальных и перпендикулярных им касательных, составляющих ускорений, показаны на плане (рис. 6).

Измерив по плану ускорений соответствующие отрезки, получим:

а_В = К_а· 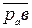 = 15 · 100 = 1500 м/с²;

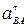 = р_а ·  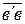= 15 · 32 = 480 м/с²;

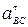 = К_а ·  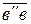= 15 · 97 = 1455 м/с².

Величины угловых ускорений звеньев определяем по формулам:

ε₂ = 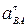/ℓ_АВ = 480/0,6 = 800 рад/с²;

ε₃ = 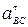/ℓ_ВС = 1455/0,4 = 3638 рад/с².

Для определения направления угловых ускорений звеньев переносим векторы касательных составляющих ускорений в соответствующие точки плана механизма (рис. 4) и укажем их направление.

ЗАКЛЮЧЕНИЕ

В результате структурно-кинематического анализа шарнирно-рычажного механизма при заданном положении кривошипа φ = 135° установлено, что механизм кривошипно-коромысловый с одной степенью подвижности, т.е. числом степеней свободы.

Траектории движения характерных точек: точки А – окружность, точки В – дуга окружности, точки S₂ – центра масс шатуна – овал. Звено 1 (кривошип) совершает равномерное вращательное движение, звенья 2 (шатун) и 3 (коромысло) движутся со значительными ускорениями. В приведённом примере шатун равноускоренно, коромысло – равнозамедленно. Данный механизм служит для преобразования вращательного движения кривошипа в возвратно-вращательное неполнооборотное движение коромысла и может быть использован для привода затворов артиллерийского орудия, насосов различного назначения, в приборах с фиксацией параметров и других целей.