Экспертным или измерительным методом
Цель: научиться определять качество продукции экспертным или измерительным методом
Краткие теоретические сведения
Измерительный метод
Измерительный метод основан на использовании для определения показателей качества товаров измерительных приборов, реактивов и других технических средств измерений. Этот метод наиболее распространен при определении единичных показателей функциональных, эргономических, экологических свойств, надежности, безопасности. Техническими средствами измерений здесь служат в основном меры и измерительные приборы.
Достоинство измерительного метода: объективность, точность и возможность выразить показатели свойств в единицах определенной размерности – килограммах, метрах, литрах, ваттах и т.д.
Недостатки измерительного метода: использование в ряде случаев довольно сложного оборудования, а также потери образцов товаров за счет их разрушения или порчи при испытаниях.
Исходные данные: табл.6 (вариант определяет преподаватель).
Таблица 6
| № вари-анта | Общее кол-во изделий N | Количество отказавших изделий n (шт.) за интервал времени ti (час) | |||||||||
| 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | 700-800 | 800-900 | 900-1000 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 1000 | 30 | 170 | 50 | 20 | 30 | 20 | 280 | 200 | 70 | 130 |
| 2 | 2500 | 80 | 320 | 300 | 20 | 80 | 600 | 600 | 110 | 210 | 200 |
| 3 | 3000 | 100 | 500 | 200 | 10 | 90 | 100 | 100 | 600 | 100 | 500 |
| 4 | 5100 | 150 | 950 | 200 | 100 | 50 | 190 | 1360 | 1100 | 250 | 750 |
| 5 | 1150 | 50 | 180 | 60 | 20 | 35 | 25 | 330 | 220 | 50 | 170 |
| 6 | 7300 | 1240 | 370 | 140 | 230 | 140 | 2060 | 1450 | 450 | 1000 | 1240 |
| 7 | 8300 | 250 | 1410 | 420 | 170 | 250 | 160 | 2320 | 1660 | 420 | 1240 |
| 8 | 300 | 9 | 51 | 15 | 6 | 9 | 6 | 84 | 60 | 15 | 45 |
| 9 | 1000 | 30 | 170 | 50 | 30 | 20 | 20 | 180 | 300 | 140 | 60 |
| 10 | 300 | 9 | 51 | 15 | 9 | 6 | 6 | 54 | 90 | 42 | 18 |
| 11 | 700 | 22 | 117 | 38 | 20 | 12 | 13 | 143 | 195 | 98 | 42 |
| 12 | 6700 | 200 | 1140 | 260 | 270 | 140 | 134 | 1206 | 2010 | 890 | 450 |
| 13 | 3700 | 110 | 630 | 190 | 110 | 70 | 80 | 660 | 1110 | 520 | 220 |
| 14 | 1200 | 40 | 200 | 60 | 36 | 24 | 24 | 216 | 360 | 168 | 72 |
| 15 | 1800 | 60 | 300 | 90 | 60 | 30 | 36 | 324 | 540 | 252 | 108 |
| 16 | 1300 | 34 | 224 | 66 | 30 | 14 | 16 | 276 | 380 | 186 | 74 |
| 17 | 13300 | 390 | 2270 | 510 | 530 | 270 | 258 | 2402 | 4010 | 1770 | 890 |
| 18 | 7300 | 210 | 1250 | 370 | 210 | 130 | 150 | 1310 | 2210 | 1030 | 430 |
| 19 | 2300 | 70 | 390 | 110 | 62 | 38 | 38 | 422 | 710 | 326 | 134 |
| 20 | 3500 | 110 | 590 | 170 | 110 | 50 | 62 | 638 | 1070 | 494 | 206 |
Пояснения к работе
1. Определяем количество работоспособных изделий на начало каждого периода по формуле:
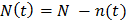
. (1)
2. Определяем статистическую оценку вероятности безотказной работы на начало каждого периода по формуле:
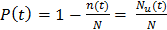. (2)
3. Определяем количество отказавших деталей нарастающим итогом на конец каждого периода по формуле:
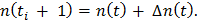(3)
4. Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле:
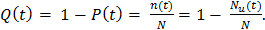(4)
5. Определяем статистическую оценку плотности вероятности отказов по формуле:
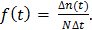(5)
6. Определяем значение интенсивности отказов по формуле:
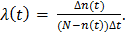(6)
7. Результаты расчета для удобства сводим в табл. 7.
Таблица 7
| Вре-менной интервал Δ t ,ч | Количе-ство от-казов за данный интервал Δ n(t) | Количе-ство ра-ботоспособных изделий на конец периода N ( t ) | Количе-ство отказа-вших изделий на конец периода | Вероят-ность безот-казной работы на конец периода P(t) | Вороят-ность отказа на конец периода Q ( t )=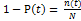 
| Плотность вероятно-сти отка-зов f ( t ) за период
·10-2
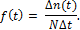
| Интенсивность отказов за пери-од λ ( t ),
·10-2
|
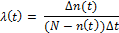
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0-100 | |||||||
| 100-200 | |||||||
| 200-300 | |||||||
| 300-400 | |||||||
| 400-500 | |||||||
| 500-600 | |||||||
| 600-700 | |||||||
| 700-800 | |||||||
| 800-900 | |||||||
| 900-1000 |
8. По данным расчета строим графики зависимости расчетных величин по времени.
Экспертный метод
Для определения значений показателей качества могут быть использованы инструментальные и экспертные методы.
Инструментальные методы применяются в ограниченных случаях, когда показатели качества представляют собой физические величины и существую измерительные инструменты (средства измерения), обладающие нормированными метрологическими характеристиками. Инструментальные определения показателей качества сводятся, таким образом, к решению обычных измерительных задач метрологии.
Экспертные методы оценивания показателей качества применяют тогда, когда использование технических средств измерения невозможно или экономически не оправдано. Экспертные методы используют, например, для оценивания эргономических и эстетических показателей, в спорте, в гуманитарных областях наук.
Экспертную оценку качеству продукции может дать один специалист, однако в целях повышения достоверности оценки предпочтения отдается групповому методу оценивания.
Какова должна быть численность экспертной группы? Теоретически эффективность групповой оценки с увеличением количества экспертов возрастает. На практике же число экспертов в группе рекомендуется не менее 7 и не более 20 человек. Слишком малое число экспертов резко увеличивает недостоверность групповой оценки, слишком большое – практически не повышая эффективность этой оценки, приводит к ненужным дебатам.
Далее остановимся на особенностях экспертных методов: метода ранговой корреляции и метода парных сравнений.
Исходные данные: задание выполняется группами (состав групп и вариант определяет преподаватель).
Вариант 1 Вариант 2
| Эксперты | К1 | К2 | К4 | К8 | К11 |
| 1 | 4 | 2 | 1 | 2 | 3 |
| 2 | 4 | 3 | 3 | 1 | 2 |
| 3 | 4 | 4 | 1 | 2 | 3 |
| 4 | 3 | 4 | 1 | 3 | 2 |
| 5 | 3 | 4 | 1 | 1 | 2 |
| 6 | 4 | 4 | 2 | 1 | 3 |
| Эксперты | К1 | К3 | К5 | К6 | К7 | К11 |
| 1 | 2 | 4 | 3 | 2 | 1 | 1 |
| 2 | 1 | 3 | 4 | 2 | 1 | 1 |
| 3 | 2 | 2 | 4 | 1 | 1 | 3 |
| 4 | 1 | 3 | 4 | 3 | 2 | 1 |
| 5 | 2 | 4 | 3 | 2 | 3 | 1 |
Вариант 3
| Эксперты | К2 | К4 | К5 | К9 | К10 |
| 1 | 1 | 2 | 4 | 2 | 3 |
| 2 | 1 | 3 | 2 | 4 | 2 |
| 3 | 1 | 4 | 2 | 2 | 3 |
| 4 | 2 | 4 | 3 | 1 | 2 |
| 5 | 2 | 4 | 3 | 1 | 2 |
| 6 | 1 | 2 | 3 | 4 | 3 |
Вариант 4 Вариант 5
| Эксперты | К1 | К3 | К5 | К6 | К7 | К11 |
| 1 | 2 | 4 | 3 | 2 | 1 | 1 |
| 2 | 1 | 3 | 4 | 2 | 1 | 1 |
| 3 | 2 | 2 | 4 | 1 | 1 | 3 |
| 4 | 1 | 3 | 4 | 3 | 2 | 1 |
| 5 | 2 | 4 | 3 | 2 | 3 | 1 |
| Эксперты | К3 | К4 | К5 | К7 | К9 |
| 1 | 1 | 3 | 2 | 4 | 2 |
| 2 | 2 | 1 | 3 | 4 | 2 |
| 3 | 1 | 2 | 1 | 4 | 3 |
| 4 | 2 | 2 | 1 | 4 | 3 |
| 5 | 2 | 1 | 3 | 4 | 2 |
| 6 | 2 | 1 | 1 | 3 | 2 |
Вариант 6
| Эксперты | К2 | К5 | К8 | К9 | К11 | К12 |
| 1 | 4 | 3 | 2 | 1 | 4 | 3 |
| 2 | 2 | 3 | 1 | 2 | 4 | 4 |
| 3 | 4 | 2 | 2 | 1 | 3 | 3 |
| 4 | 3 | 3 | 2 | 1 | 4 | 4 |
| 5 | 2 | 2 | 1 | 1 | 4 | 3 |
Пояснение к работе
1. Определяем наиважнейший и следующий по значимости критерий и оцениваем степень согласованности мнений экспертов. Результаты экспертного опроса с пятью рангами заданы в таблицах по вариантам.
Экспертный опрос на основе метода ранговой корреляции основан на том, что каждый из m экспертов, участвующих в опросе, присваивает каждому из оцениваемых n объектов (критериев) некоторое ранговое число (оценку).
При этом наиболее важный критерий получает ранг (оценку) 1, следующий – ранг 2 и т.д в порядке убывания значимости.
Если число рангов k не совпадает с числом объектов n, то эксперт присваивает разным объектам один и тот же ранг.
Через uij обозначается ранговое число, которое i-й эксперт присвоил j-му объекту, причем i = 1,2,……,n .
Чаще всего число рангов меньше, чем число оцениваемых объектов (k < n), поэтому для обеспечения возможности применения метода ранговой корреляции объектам присваивают так называемые нормированные ранги.
Рассмотрим подробнее процедуру нормирования. В каждой строке ранговым числам присваиваются последовательно неповторяющиеся места, а затем определяется среднее арифметическое суммы мест, которые занимают объекты с одинаковыми рангами. Это значение записывается в новую нормированную матрицу на место соответствующего ранга. Места для удобства подписываются в исходной матрице в верхнем правом углу.
Рассмотрим пример, когда 5 экспертов оценивают 6 критериев по четырехбалльной системе, т.е. наименее важному критерию присваивается ранг, равный 4. Тогда результаты экспертного опроса можно представить в табл. 8.
Таблица 8
Результаты опроса
| Эксперты | Критерии | |||||
| К1 (№1) | К3 (№2) | К4 (№3) | К8 (№4) | К10 (№5) | К12 (№6) | |
| 1 | 2 3 | 3 4 | 1 1 | 4 6 | 1 2 | 3 5 |
| 2 | 1 1 | 2 2 | 2 3 | 3 5 | 2 4 | 4 6 |
| 3 | 1 | 4 | 1 | 3 | 2 | 4 |
| 4 | 2 | 3 | 2 | 4 | 3 | 2 |
| 5 | 2 | 2 | 1 | 3 | 2 | 4 |
Например, для первого эксперта ранг 1 повторяется два раза, т.к он присвоен третьему и пятому объектам (К4 и К10), которые, соответственно, имеют места 1 и 2. Следовательно, нормированный ранг этих объектов, представляющий собой среднее арифметическое их мест, равен (1+2)/2=1,5. Это значение в новой матрице будет стоять в первой строке в третьей и пятой ячейках следующей табл.2.
Ранговое число 2 повторяется в первой строке один раз, поэтому ему присваивается следующее место – 3, которое и будет новым нормированным рангом (первая ячейка). Рангу 3 будут присвоены места 4 и 5, а значение (4+5)/2=4,5 займет в новой матрице вторую и шестую ячейки, где в первоначальной матрице находилась цифра 3. Четвертому рангу, который повторяется один раз, соответствует место 6, которое и будет его нормированным значением. Во второй строке первый ранг, встречающийся один раз, не меняется; рангу 2 соответствуют места 2-4 и нормированное значение (2+3+4)/3=3; встречающимся по одному разу рангам 3 и 4 соответствует нормированные значения, равные их местам, - соответственно 5 и 6.
Таким же образом определяются нормированные ранги и для остальных объектов. В результате нормирования матрица приобретает вид табл.9.
Последняя строка табл.9 содержит суммы нормированных рангов для каждого критерия.
Таблица 9.
| Эксперты | Критерии | ||||||
| К1 | К3 | К4 | К8 | К10 | К12 | Ti | |
| 1 | 3 | 4,5 | 1,5 | 6 | 1,5 | 4,5 | 12 |
| 2 | 1 | 3 | 3 | 5 | 3 | 6 | 24 |
| 3 | 1,5 | 5,5 | 1,5 | 4 | 3 | 5,5 | 12 |
| 4 | 2,5 | 4,5 | 1 | 6 | 4,5 | 2,5 | 12 |
| 5 | 3 | 3 | 1 | 5 | 3 | 6 | 24 |
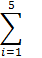
| 11 | 20,5 | 8 | 26 | 15 | 14,5 | 84 |
В полученную матрицу вводится столбец Тi, который будет далее использован для оценки достоверности полученных результатов. Величины Тi, рассчитываются по формуле:
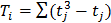(7)
где, tj – число повторений j-го рангового числа в i-й строке.
В примере с четырехбалльной системой оценок число слагаемых в формуле (7) равно 4.
Для первого эксперта ранги 1,2,3 и 4 повторялись 2,1,2 и 1 раз соответственно:
Т1 = (23 - 2) + (13 - 1) + (23 - 2) + (13 – 1) = 12.
Для второго эксперта:
Т2 = (13 – 1) + (33 – 3) + (13 – 1) + (13 – 1) = 24.
Аналогично вычисляются все значения последнего столбца табл.9.
Поскольку более важный критерий имеет меньший ранг, то наиважнейшему критерию будет соответствовать минимальная сумма нормированных рангов, т.е. все эксперты оценили этот критерий относительно небольшим числом.
Как видно из вышеприведенного примера, первое место и наибольшее предпочтение должны быть отданы третьему объекту, второе место – первому, третье место – шестому, четвертое место – пятому, пятое место – второму, шестое место – четвертому и т.д
Степень согласованности мнений экспертов оценивается с помощью коэффициента конкордации Кендалла, который рассчитывается по формуле:
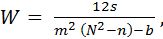(8)
где s и b вычисляются следующим образом :
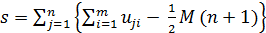(9)
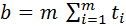, (10)
Используемые здесь суммы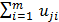 
и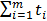 
берутся из последней строки табл.6.
Коэффициент Кендалла может изменяться от 0 (при отсутствии согласованности экспертов) до 1 (при полном единодушии экспертов), причем чем ближе его значение к единице, тем выше согласованность мнений экспертов относительно оцениваемых объектов.
При W > 0,5 мнение экспертов согласовано более чем на 50 % , следовательно, результаты опроса могут быть использованы в дальнейшем. При W ≤ 0,5 мнение не согласованно, поэтому необходимо проводить новый экспертный опрос.
2. Каждый из экспертов заполнил верхнюю часть своей таблицы парных сравнений. Заполните нижние части таблиц соответствующими элементами. Определите наилучший технологический вариант и степень согласованности мнений экспертов.
Вариант 1
| - | 0 | 1 | 1 |
| - | 1 | 0 | 0 |
| - | 1 | 1 | 1 |
| - | 0 | 1 | 1 |
| - | 1 | 1 | 1 |
| - | 0 | 1 | - | 0 | 0 | - | 1 | 1 | - | 1 | 1 | - | 1 | 0 | |||||||||
| - | 0 | - | 0 | - | 1 | - | 0 | - | 0 | ||||||||||||||
| - | - | - | - | - |
Вариант 2
| - | 0 | 0 | 0 | 0 |
| - | 0 | 1 | 0 | 0 |
| - | 0 | 0 | 0 | 0 |
| - | 0 | 0 | 0 | 0 |
| - | 0 | 0 | 1 | - | 0 | 1 | 0 | - | 0 | 0 | 0 | - | 0 | 1 | 1 | |||||||
| - | 1 | 0 | - | 0 | 0 | - | 1 | 1 | - | 1 | 0 | |||||||||||
| - | 0 | - | 0 | - | 0 | - | 0 | |||||||||||||||
| - | - | - | 0 |
Вариант 3
| - | 0 | 1 | 1 |
| - | 1 | 0 | 0 |
| - | 1 | 1 | 1 |
| - | 0 | 1 | 1 |
| - | 1 | 1 | 1 |
| - | 0 | 1 | - | 0 | 0 | - | 1 | 1 | - | 1 | 1 | - | 1 | 0 | |||||||||
| - | 0 | - | 0 | - | 1 | - | 0 | - | 0 | ||||||||||||||
| - | - | - | - | - |
Вариант 4
| - | 0 | 0 | 0 | 0 |
| - | 0 | 1 | 0 | 0 |
| - | 0 | 0 | 0 | 0 |
| - | 0 | 0 | 0 | 0 |
| - | 0 | 0 | 1 | - | 0 | 1 | 0 | - | 0 | 0 | 0 | - | 0 | 1 | 1 | |||||||
| - | 1 | 0 | - | 0 | 0 | - | 1 | 1 | - | 1 | 0 | |||||||||||
| - | 0 | - | 0 | - | 0 | - | 0 | |||||||||||||||
| - | - | - | 0 |
Вариант 5
| - | 0 | 1 | 1 |
| - | 1 | 0 | 0 |
| - | 1 | 1 | 1 |
| - | 0 | 1 | 1 |
| - | 1 | 1 | 1 |
| - | 0 | 1 | - | 0 | 0 | - | 1 | 1 | - | 1 | 1 | - | 1 | 0 | |||||||||
| - | 0 | - | 0 | - | 1 | - | 0 | - | 0 | ||||||||||||||
| - | - | - | - | - |
Вариант 6
| - | 0 | 0 | 0 | 0 |
| - | 0 | 1 | 0 | 0 |
| - | 0 | 0 | 0 | 0 |
| - | 0 | 0 | 0 | 0 |
| - | 0 | 0 | 1 | - | 0 | 1 | 0 | - | 0 | 0 | 0 | - | 0 | 1 | 1 | |||||||
| - | 1 | 0 | - | 0 | 0 | - | 1 | 1 | - | 1 | 0 | |||||||||||
| - | 0 | - | 0 | - | 0 | - | 0 | |||||||||||||||
| - | - | - | 0 |
Эксперты в соответствии с целевой установкой (выбранным критерием оптимальности) попарно оценивают предложенные варианты.
Число экспертов – m, количество вариантов – n.
Каждый эксперт заполняет одну таблицу (форма табл. 9), элементы которой: aij=1, если i-й вариант лучше j-го, aij=0, если i-й вариант хуже j-го.
Вариант, находящийся в определенной строке, поочередно сравнивается с вариантами всех столбцов. Вариант сам с собой не сравнивается, поэтому диагональные ячейки табл. 9 не заполняются.
Например, если 4-й вариант лучше второго, то a42 = 1, тогда, соответственно, второй вариант хуже четвертого и а24 = 0.
Таблица 10
Пример заполненной таблицы эксперта
| Эксперт 1 |
| Эксперт 2 |
| Эксперт 3 |
| Эксперт 4 |
| Эксперт 5 | ||||||||||||||||||||
| В | 1 | 2 | 3 | 4 | В | 1 | 2 | 3 | 4 | В | 1 | 2 | 3 | 4 | В | 1 | 2 | 3 | 4 | В | 1 | 2 | 3 | 4 | ||||
| 1 | - | 0 | 0 | 0 | 1 | - | 0 | 0 | 0 | 1 | - | 0 | 0 | 0 | 1 | - | 0 | 0 | 0 | 1 | - | 0 | 0 | 0 | ||||
| 2 | 1 | - | 0 | 1 | 2 | 1 | - | 1 | 0 | 2 | 1 | - | 1 | 0 | 2 | 1 | - | 0 | 1 | 2 | 1 | - | 0 | 0 | ||||
| 3 | 1 | 1 | - | 0 | 3 | 1 | 1 | - | 1 | 3 | 1 | 0 | - | 1 | 3 | 1 | 1 | - | 1 | 3 | 1 | 1 | - | 0 | ||||
| 4 | 1 | 0 | 1 | - | 4 | 1 | 0 | 0 | - | 4 | 1 | 1 | 0 | - | 4 | 1 | 0 | 0 | - | 4 | 1 | 0 | 1 | - | ||||
Таким образом, всегда выполняется условие аij + aji = 1, и эксперт может заполнить только часть таблицы (выше или ниже диагонали), а в оставшейся части таблицы можно записать соответствующие противоположные элементы.
Все m заполненных таблиц складываются поэлементно. Тем самым осуществляется переход к табл. 11. В результате получается таблица с элементами bij, где максимальный элемент не больше m.
Если все эксперты решили, что i-й вариант лучше j-го, то bij = m, а противоположный элемент bji = 0. Если, например, два из них с этим не согласны, то bij = m – 2 и bji = 2.
Для результирующей таблицы выполняется условие bij + bji = m.
Таблица 11
Результирующая
| Вариант | 1 | 2 | 3 | 4 | Сумма | Ранг |
| 1 | - | 0 | 0 | 0 | 0 | 4 |
| 2 | 5 | - | 1 | 4 | 10 | 2 |
| 3 | 5 | 4 | - | 3 | 12 | 1 |
| 4 | 5 | 1 | 2 | - | 8 | 3 |
Сумма в каждой строке показывает, сколько всего раз этот вариант предпочли всем остальным. Максимальное значение суммы соответствует наилучшему варианту технологии, которому присваивается первый ранг, и далее по порядку.
Степень согласованности мнений экспертов оценивается с помощью коэффициента, который рассчитывается по формуле:
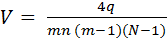, (11)
где q вычисляется по формуле:
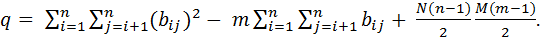(12)
При вычислении q суммируются элементы таблицы, для которых номер столбца j больше номера строки i – это элементы, расположенные выше основной диагонали.
Мнение экспертов считается согласованным, если V>0,5.
Порядок выполнения
1. Рассчитать статистические оценки показателей безотказности.
2. Определить согласованность мнений экспертов.
3. Заполнить таблицу по результатам расчетов.
Содержание отчета
1. Результаты расчета статистических оценок показателей безотказности.
2. Заполненная результирующая таблица.
3. Расчет степени согласованности мнений экспертов.
Контрольные вопросы
1. В чем заключается сущность метода ранговой корреляции?
2. Для чего необходим коэффициент V и чему он может быть равен?
3. Можно ли разным критериям присваивать одинаковые ранги?
4. Чему в результирующей таблице равен элемент b32, если b23 =0?
5. Почему наиважнейшему критерию соответствует минимальная сумма нормированных рангов?
6. Каким образом проводится нормирование?
7. Для чего необходимо использовать коэффициент W и какие значения он может принимать?
8. Каким элементам таблицы в методе парных сравнений эксперт может не заполнять и почему?
9. В чем заключается сущность метода парных сравнений?
Практическое занятие № 7
Дата: 2018-11-18, просмотров: 972.
