Вопросы теории
- Понятие алгебраического числа над полем.
- Минимальный многочлен алгебраического числа.
- Степень алгебраического числа.
- Алгебраическая иррациональность над полем.
- Алгоритм Евклида.
- Алгоритм избавления от алгебраической иррациональности в знаменателе дроби.
Образцы решения задач
Задача 1. Доказать непосредственно (исходя из определения алгебраического числа), что каждое из чисел
а) 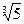 4 б)
4 б) 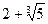 ; в) – 1 +2i; г) – 1 +i
; в) – 1 +2i; г) – 1 +i 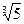
является алгебраическим, и найти его степень (над Q).
Решение. Число 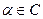 называется алгебраическим над полем Q (или просто алгебраическим), если оно является корнем некоторого многочлена с коэффициентами из Q.
называется алгебраическим над полем Q (или просто алгебраическим), если оно является корнем некоторого многочлена с коэффициентами из Q.
Многочлен р(х) 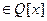 наименьшей степени, корнем которого является данное алгебраическое число α, называется минимальным многочленом числа α, степень этого многочлена называется степенью числа α (над Q). Многочлен р (х) определен с точностью до числового множителя
наименьшей степени, корнем которого является данное алгебраическое число α, называется минимальным многочленом числа α, степень этого многочлена называется степенью числа α (над Q). Многочлен р (х) определен с точностью до числового множителя 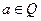 . Минимальный многочлен всегда неприводим (над Q); обратно, неприводимый многочлен, имеющий α своим корнем, является минимальным многочленом числа α.
. Минимальный многочлен всегда неприводим (над Q); обратно, неприводимый многочлен, имеющий α своим корнем, является минимальным многочленом числа α.
а) Для числа α = 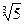 имеем:
имеем: 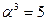 , то есть α есть корень многочлена
, то есть α есть корень многочлена 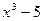 . Следовательно, α - алгебраическое число. Так как многочлен
. Следовательно, α - алгебраическое число. Так как многочлен  неприводим над Q, то он является минимальным многочленом числа α; степень α над Q равна 3.
неприводим над Q, то он является минимальным многочленом числа α; степень α над Q равна 3.
б) Для α = 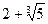 имеем:
имеем: 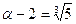 , откуда следует:
, откуда следует: 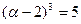 . Таким образом, число α является корнем многочлена
. Таким образом, число α является корнем многочлена 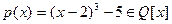 и, следовательно, алгебраическим числом. Многочлен р (х) неприводим над Q, поэтому степень α равна 3.
и, следовательно, алгебраическим числом. Многочлен р (х) неприводим над Q, поэтому степень α равна 3.
в) Для α = – 1 +2i имеем: α + 1 = 2i и, следовательно, 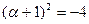 . Отсюда видно, что α является корнем многочлена
. Отсюда видно, что α является корнем многочлена 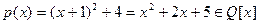 , а значит, алгебраическим числом. Так как р (х) неприводим над Q, то степень α равна 2.
, а значит, алгебраическим числом. Так как р (х) неприводим над Q, то степень α равна 2.
г) Для α = – 1 +i 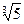 можем записать: α + 1 = i
можем записать: α + 1 = i 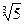 =>
=>  .
.
Следовательно, α – корень многочлена 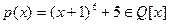 . Это означает, что α - алгебраическое число. Так как р (х) неприводим над Q (чтобы в этом убедиться, достаточно применить к многочлену
. Это означает, что α - алгебраическое число. Так как р (х) неприводим над Q (чтобы в этом убедиться, достаточно применить к многочлену 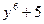 признак Эйзенштейна), то степень α равна 6.
признак Эйзенштейна), то степень α равна 6.
Задача 2. В поле Q (α), где α = 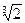 , найти выражение для числа
, найти выражение для числа 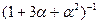 в виде
в виде  .
.
Решение. Фактически здесь ставится задача освободиться от корней в знаменателе дроби
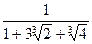 ,
,
или, как еще говорят, «освободиться от алгебраической иррациональности в знаменателе». Задачу можно решить двумя способами.
I способ. Будем искать числа  такие, чтобы
такие, чтобы  .
.
В силу формулы  неизвестные
неизвестные 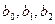 должны удовлетворять уравнению
должны удовлетворять уравнению
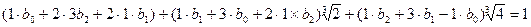
или, если учесть, что числа 1, 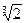 ,
, 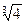 линейно независимы над Q, системе уравнений
линейно независимы над Q, системе уравнений
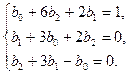
Решая эту систему, находим:
 .
.
Ответ. (1 + 3 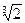 +
+ 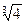 )
)  =
=  .
.
II способ. Число 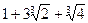 есть значение многочлена
есть значение многочлена  при х = α =
при х = α = 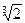 . Этот многочлен взаимно прост с многочленом р (х) =
. Этот многочлен взаимно прост с многочленом р (х) =  (минимальным многочленом числа α), так как р (х) неприводим, а
(минимальным многочленом числа α), так как р (х) неприводим, а 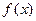 не делится на р (х). Следовательно, существуют многочлены u (x) и v (x) такие, что
не делится на р (х). Следовательно, существуют многочлены u (x) и v (x) такие, что
u (x) 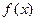 + v (x) р (х) = 1.
+ v (x) р (х) = 1.
Полагая в этом равенстве х = α, будем иметь:
u (α)  = 1
= 1
или

- искомое представление для числа 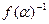 . Итак, остается лишь найти многочлены u (x) и v (x).
. Итак, остается лишь найти многочлены u (x) и v (x).
Применим к 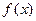 и р (х) алгоритм Евклида:
и р (х) алгоритм Евклида:
1) р (х) = 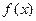 (х – 3) + r (x), где r (x) = 8х +1;
(х – 3) + r (x), где r (x) = 8х +1;
2) 8 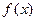 = r (x)
= r (x) 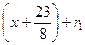 , где
, где 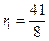 .
.
Получим:
 .
.
Полагая в последнем равенстве х = α, находим:
 ,
,
или
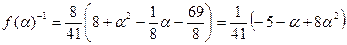 .
.
Ответ, разумеется, получился тот же самый, что и при I способе решения.
Задача 3. Освободиться от α в знаменателе дроби  , если α – корень уравнения
, если α – корень уравнения  .
.
Решение. Положим р (х) =  . С помощью известных нам приемов определяем, что многочлен р (х) не имеет рациональных корней; из этого, поскольку степень р (х) равна 3, следует, что р (х) неприводим над Q. Знаменатель данной дроби
. С помощью известных нам приемов определяем, что многочлен р (х) не имеет рациональных корней; из этого, поскольку степень р (х) равна 3, следует, что р (х) неприводим над Q. Знаменатель данной дроби  не равен нулю, так как α ≠ - 1 (число – 1 не является корнем многочлена р (х)). Это означает, что многочлен
не равен нулю, так как α ≠ - 1 (число – 1 не является корнем многочлена р (х)). Это означает, что многочлен 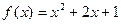 взаимно прост с р (х) (в противном случае
взаимно прост с р (х) (в противном случае 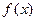 и р (х) имели бы общий корень – 1, что, как мы видели, невозможно). Пользуясь этим, будем искать многочлены u (x) и v (x) такие, что
и р (х) имели бы общий корень – 1, что, как мы видели, невозможно). Пользуясь этим, будем искать многочлены u (x) и v (x) такие, что
u (x) 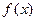 + v (x) р (х) = 1.
+ v (x) р (х) = 1.
Применяем к р (х) и 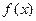 алгоритм Евклида. Деля р (х) на
алгоритм Евклида. Деля р (х) на 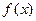 с остатком, получим:
с остатком, получим:
р (х) = 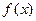 (х – 1) + r (х),
(х – 1) + r (х),
где r (х) = 4х + 5. Далее находим:
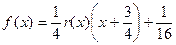 .
.
Отсюда имеем:
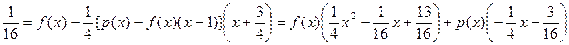 .
.
При х = α из последнего равенства получаем:
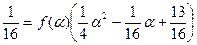 ,
,
или 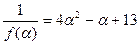 .
.
Умножая обе части равенства на число 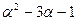 , то есть на числитель данной в задаче дроби, получим:
, то есть на числитель данной в задаче дроби, получим:
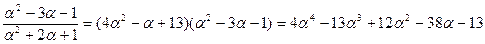 .
.
В принципе мы привели дробь к нужному виду. Однако можно еще упростить полученное выражение, воспользовавшись тем, что 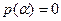 . Делим с остатком многочлен
. Делим с остатком многочлен 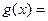
 на р (х) =
на р (х) =  . Получаем:
. Получаем:
 р (х) (4х – 17) + S(x),
р (х) (4х – 17) + S(x),
где S(x) = 17х² - 3х + 55. При х = α имеем:
 .
.
Ответ. 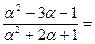
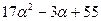 .
.
Задачи для решения.
1. Доказать непосредственно, что число α является алгебраическим, и найти минимальный многочлен числа α:
а) α = 1; б) α =i; в) α = - 1+ 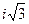 ; г) α = 1 -
; г) α = 1 - 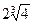 ;
;
д) α = 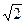 +
+  ; е) α =
; е) α = 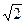 +i
+i 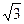 ; ж) α =
; ж) α =  ;
;
з) α = 1+ 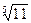 ; и) α =
; и) α = 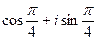 ; к) α =
; к) α = 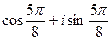 .
.
2. Доказать непосредственно, что число α является алгебраическим, и найти многочлен над Q (не обязательно минимальной степени), корнем которого является α:
а) α = 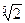 -
- 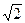 ; б) α =
; б) α = 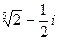 ; в) α =
; в) α =  -i
-i 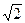 .
.
3. Доказать непосредственно, что если число α алгебраическое, то каждое из чисел 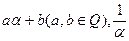 (если α ≠ 0), α² снова алгебраическое.
(если α ≠ 0), α² снова алгебраическое.
4. Являются ли алгебраически сопряженными числа: а) 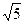 и -
и - 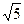 ; б)
; б) 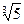 и -
и - 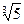 ; в)
; в) 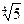 и -
и - 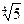 ; г)
; г) 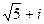 и
и 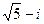 ; д)
; д) 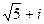 и -
и -  ?
?
5. Освободиться от иррациональности в знаменателе дроби:
а) 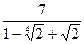 ; б)
; б)  .
.
6. Освободиться от алгебраической иррациональности в знаменателе дроби:
а) 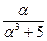 , где
, где 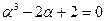 ;
;
б) 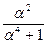 , где
, где 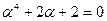 ;
;
в)  , где
, где 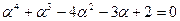 .
.
7. Найти многочлен над Q, корнем которого является число 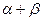 , если известны минимальные многочлены для
, если известны минимальные многочлены для 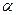 и
и 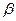 :
:
а)  ;
;
б) 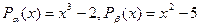 ;
;
в) 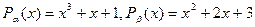 .
.
Тема 14. Расширения полей.
Вопросы теории
1. Расширение поля.
2. Простое алгебраическое расширение поля.
3. Составное алгебраическое расширение поля.
4. Размерность расширения.
Образцы решения задач
Задача 1. Поле Q последовательно расширяется – сначала с помощью числа 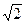 , затем с помощью
, затем с помощью  : Q Ì Q1 Ì Q2, где Q1 = Q(
: Q Ì Q1 Ì Q2, где Q1 = Q(  ),Q2 = Q1 (
),Q2 = Q1 ( 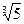 ).
).
Доказать, что такое расширение может быть достигнуто в один шаг – с помощью числа 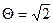 +
+ 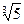 , то есть что Q(
, то есть что Q(  )(
)( 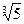 )=Q(
)=Q( 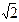 +
+ 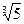 ).
).
Решение. Согласно теореме о простоте составного расширения любые два последовательно произведенных простых алгебраических расширения поля Р

(  алгебраично над Р, а
алгебраично над Р, а 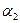 - над Р1) могут быть заменены одним, то есть существует такое число
- над Р1) могут быть заменены одним, то есть существует такое число 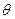 , алгебраическое над Р, что
, алгебраическое над Р, что
 .
.
Наша задача – показать, что в случае, когда Р есть поле Q рациональных чисел, а 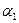 =
= 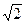 и
и 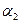 =
= 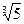 , в качестве
, в качестве  можно взять
можно взять 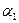 +
+ 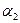 .
.
Достаточно показать, что поле Q ( 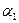 +
+ 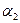 ) содержит каждое из чисел
) содержит каждое из чисел 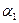 и
и 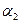 , так как в этом случае оно будет содержать поле Q1 = Q(
, так как в этом случае оно будет содержать поле Q1 = Q(  ) и число
) и число 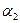 , а значит, и поле Q2 = Q1(
, а значит, и поле Q2 = Q1( 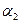 ); тогда из Q (
); тогда из Q ( 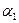 +
+ 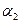 ) É Q2 и Q (
) É Q2 и Q ( 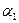 +
+ 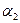 )Ì Q2 (второе включение является очевидным) будет следовать: Q (
)Ì Q2 (второе включение является очевидным) будет следовать: Q ( 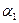 +
+ 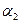 ) = Q2.
) = Q2.
На самом деле достаточно показать еще меньше – что поле Q (  +
+ 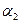 ) содержит
) содержит 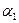 , так как
, так как 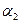 тогда будет принадлежать полю Q (
тогда будет принадлежать полю Q (  +
+ 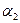 ) как разность двух чисел из этого поля (
) как разность двух чисел из этого поля ( 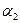 = (
= ( 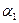 +
+ 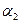 ) -
) - 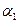 ).
).
Для сокращения записей обозначим поле Q ( 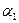 +
+ 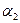 ) через L. Допустим, рассуждая от противного, что число
) через L. Допустим, рассуждая от противного, что число 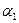 =
= 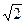 не принадлежит L. Рассмотрим два многочлена над L:
не принадлежит L. Рассмотрим два многочлена над L:
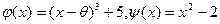
(напомним, что 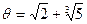 ). Каждый из них имеет одним из своих корней число
). Каждый из них имеет одним из своих корней число 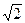 :
:
 ;
; 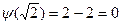 .
.
Проверим, что других общих корней многочлены 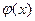 и
и  не имеют.
не имеют.
Действительно, корни  - это числа
- это числа 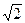 , -
, -  .
.
Корнями же многочлена 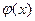 являются корни уравнения
являются корни уравнения 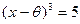 , то есть числа
, то есть числа
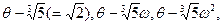
где 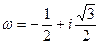 - корень кубический из 1. Следовательно, мы должны проверить, что ни одно из чисел
- корень кубический из 1. Следовательно, мы должны проверить, что ни одно из чисел 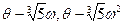 не равно -
не равно -  . Но это очевидно, так как числа
. Но это очевидно, так как числа 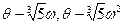 не являются действительными (коэффициент при i отличен от нуля).
не являются действительными (коэффициент при i отличен от нуля).
Поскольку, таким образом, единственный общий корень многочленов 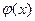 и
и 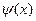 в поле С есть
в поле С есть 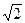 , то (нормированный) наибольший общий делитель многочленов
, то (нормированный) наибольший общий делитель многочленов  и
и 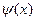 в кольце С [x] есть
в кольце С [x] есть
D (х) = х - 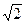 .
.
Этот же самый многочлен должен быть (нормированным) НОД многочленов 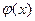 и
и  также и в кольце L [x]. Следовательно, все коэффициенты этого многочлена, в частности
также и в кольце L [x]. Следовательно, все коэффициенты этого многочлена, в частности
- 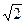 , принадлежат полю L. Тем самым и число
, принадлежат полю L. Тем самым и число 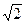 принадлежат L, что и требовалось показать.
принадлежат L, что и требовалось показать.
Задача 2. Найти выражение числа 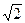 в виде
в виде  , где
, где 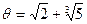 , а f (x), g (x) Î Z [x].
, а f (x), g (x) Î Z [x].
Решение. Сам факт принадлежности числа 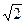 полю Q (
полю Q (  ) был установлен в задаче 1. Наша цель теперь – найти «явное» выражение числа
) был установлен в задаче 1. Наша цель теперь – найти «явное» выражение числа 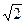 через
через 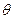 .
.
Рассмотрим снова многочлены  и
и  из (1). При решении задачи 1 мы показали, что нормированный НОД этих многочленов есть
из (1). При решении задачи 1 мы показали, что нормированный НОД этих многочленов есть
D (х) = х -  .
.
С другой стороны, НОД можно найти, применяя к  и
и  алгоритм Евклида. Для этого делим сначала
алгоритм Евклида. Для этого делим сначала  на
на 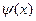 (с остатком):
(с остатком):
__ 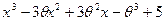 çх² - 2
çх² - 2
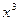 - 2х çх -
- 2х çх - 
___________________________________________________
__ 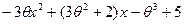
 + 60
+ 60
____________________________________________________________
( 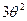 +2)х – (
+2)х – ( 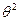 +60 – 5)
+60 – 5)
Мы получили в остатке многочлен
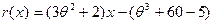
1-й степени. Поскольку ранее уже было доказано, что НОД имеет степень 1, то многочлен 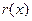 и должен быть как раз НОД многочленов
и должен быть как раз НОД многочленов  и
и  . Следовательно, многочлены
. Следовательно, многочлены
D (х) и 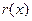 ассоциированы (отличаются лишь численным множителем):
ассоциированы (отличаются лишь численным множителем):
D (х) = 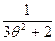
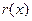 ,
,
или  .
.
Отсюда имеем: 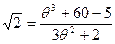 ,
,
что и дает искомое выражение для числа 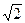 .
.
Задача 3. Пусть Q Ì Q1 Ì Q2, где Q1 = Q( 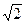 ),Q2 = Q1 (
),Q2 = Q1 ( 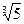 ). Найти степень поля Q2 относительно Q (то есть размерность Q2 над Q).
). Найти степень поля Q2 относительно Q (то есть размерность Q2 над Q).
Решение. Справедлива теорема: если поле Р 1 – конечное расширение поля Р, а поле Р 2 - конечное расширение Р 1, то
 (1)
(1)
В нашем случае, очевидно,  . Покажем, что
. Покажем, что
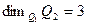 . (2)
. (2)
Чтобы доказать равенство (2), достаточно проверить, что многочлен  3-й степени, имеющий число
3-й степени, имеющий число 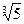 своим корнем, неприводим над Q1. Предположим, что это неверно, то есть что
своим корнем, неприводим над Q1. Предположим, что это неверно, то есть что 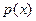 приводим. Тогда один из неприводимых множителей многочлена
приводим. Тогда один из неприводимых множителей многочлена 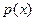 должен быть первой степени, и, следовательно, один из корней многочлена
должен быть первой степени, и, следовательно, один из корней многочлена 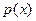 должен принадлежать Q. Таким корнем является, конечно, действительное значение
должен принадлежать Q. Таким корнем является, конечно, действительное значение 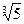 (так как все числа из Q1 действительны). Но число
(так как все числа из Q1 действительны). Но число 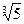 не может принадлежать Q1, так как его степень над Q равна 3, в то время как степень любого числа из Q1 (над полем Q) не выше 2. Полученное противоречие доказывает (2).
не может принадлежать Q1, так как его степень над Q равна 3, в то время как степень любого числа из Q1 (над полем Q) не выше 2. Полученное противоречие доказывает (2).
На основании формулы (1) можем теперь записать:
 . (3)
. (3)
Замечание. Сопоставив (3) с тем фактом, что  , мы можем вывести заключение, что степень числа
, мы можем вывести заключение, что степень числа 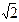 +
+ 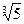 над полем Q равна 6. Это означает, что многочлен 6-й степени (над полем Q), имеющий своим корнем число
над полем Q равна 6. Это означает, что многочлен 6-й степени (над полем Q), имеющий своим корнем число  +
+ 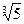 , неприводим.
, неприводим.
Задачи для решения.
1. Пусть p и q – натуральные числа, причем  и
и 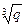 - не целые. Доказать, что
- не целые. Доказать, что
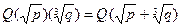 .
.
2. Найти выражение для каждого из чисел 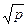 и
и  через
через 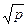 +
+ 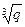 :
:
а) р = 3, q = 6; б) р = 7, q = 4; в) р = 3, q = 3.
3. Пусть p и q – натуральные числа, причем отношение чисел 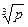 и
и 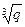 (действительных значений) не является рациональным числом. Доказать, что
(действительных значений) не является рациональным числом. Доказать, что 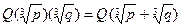 .
.
4. Используя условие задачи 3, найти выражение для каждого из чисел 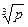 и
и 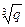 через
через  +
+ 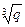 :
:
а) р = 3, q = 7; б) р = 5, q = 12.
Литература
1. Кострикин А. И. Введение в алгебру. В 3-х книгах. Кн. 3: Основные структуры алгебры. – М.: МЦНМО, 2009.
2. Курош А.Г. Курс высшей алгебры. 17-е издание, СПб.- Издательский Дом «Лань».
3. Окунев Л.Я. Высшая алгебра. 3-е издание. СПб.- Издательский Дом «Лань», 2009. 336с.
4. Окунев Л.Я. Сборник задач по высшей алгебре. 2-е издание. СПб.- Издательский Дом «Лань» 2009.
5. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. 17-е издание. СПб. - Издательский Дом «Лань» 288 с.
Дата: 2018-11-18, просмотров: 1720.