Вопросы теории
- Гомоморфизм групп.
- Свойства гомоморфизма.
- Ядро гомоморфизма.
- Биективное отображение.
- Изоморфизм групп.
- Свойства изоморфизма.
Образцы решения задач
Задача 1. Доказать, что мультипликативную группу М невырожденных матриц порядка п (п ≥1) можно гомоморфно отобразить на мультипликативную группу R \ {0} действительных чисел, отличных от нуля.
Решение. Отобразим группу М в группу R \ {0} по правилу 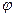 , которое каждой матрице А Î М ставит в соответствие ее определитель çАç - элемент из R \ {0}. Так как при этом отображении для любого заданного элемента из R \ {0} полный прообраз есть непустое множество (так как существует бесконечно много матриц из М, определитель которых равен заданному действительному числу), то
, которое каждой матрице А Î М ставит в соответствие ее определитель çАç - элемент из R \ {0}. Так как при этом отображении для любого заданного элемента из R \ {0} полный прообраз есть непустое множество (так как существует бесконечно много матриц из М, определитель которых равен заданному действительному числу), то 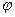 является отображением М на R \ {0}. Более того, такое отображение сохраняет операцию. Действительно, если А, В – любые элементы из группы М, то и АВ Î М, и по теореме об определителе произведения матриц получим:
является отображением М на R \ {0}. Более того, такое отображение сохраняет операцию. Действительно, если А, В – любые элементы из группы М, то и АВ Î М, и по теореме об определителе произведения матриц получим:
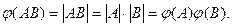
Итак, 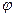 есть отображение группы М на группу R \ {0}, сохраняющее операцию, то есть гомоморфное отображение.
есть отображение группы М на группу R \ {0}, сохраняющее операцию, то есть гомоморфное отображение.
Задачи для решения
1.Докажите, что если  G→F – гомоморфизм группы G на группу F и при этом группа G коммутативна, то и группа F коммутативна. Верно ли обратное утверждение?
G→F – гомоморфизм группы G на группу F и при этом группа G коммутативна, то и группа F коммутативна. Верно ли обратное утверждение?
2.Докажите, что если 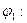 G1→G2 и
G1→G2 и  G2→G3 гомоморфизмы, то и
G2→G3 гомоморфизмы, то и 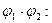 G1→ G3 – гомоморфизм.
G1→ G3 – гомоморфизм.
3.Аддитивная группа Z гомоморфно отображена на циклическую группу
G = (g) = 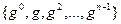 . Какие элементы из Z отображаются на элемент
. Какие элементы из Z отображаются на элемент 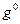 , какие – на элемент g при этом гомоморфизме? Найдите ядро гомоморфизма.
, какие – на элемент g при этом гомоморфизме? Найдите ядро гомоморфизма.
4.Почему аддитивную группу Z можно гомоморфно отобразить на знакопеременную группу 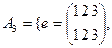
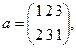
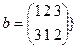 ?
?
5. Докажите, что симметрическая группа S3 третьей степени является гомоморфным образом симметрической группы S4 четвертой степени.
6. Докажите, что аддитивную группу всех функций вида 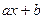
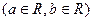 можно гомоморфно отобразить на аддитивную группу R. Каково ядро этого гомоморфизма?
можно гомоморфно отобразить на аддитивную группу R. Каково ядро этого гомоморфизма?
7. Докажите, что аддитивную группу 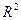 всех арифметических двумерных векторов с действительными компонентами можно гомоморфно отобразить на аддитивную группу R. Единственно ли такое отображение?
всех арифметических двумерных векторов с действительными компонентами можно гомоморфно отобразить на аддитивную группу R. Единственно ли такое отображение?
8. Докажите, что отображение 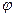 , заданное правилом
, заданное правилом 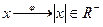 , является гомоморфизмом группы R \ {0} на
, является гомоморфизмом группы R \ {0} на 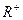 (обе группы – мультипликативные).
(обе группы – мультипликативные).
9. Докажите, что при гомоморфизме 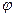 группы G1 на группу G2: а) группа G1 некоммутативна, если некоммутативна группа G2; б) группа G1 бесконечна, если бесконечна группа G2; в) элемент а
группы G1 на группу G2: а) группа G1 некоммутативна, если некоммутативна группа G2; б) группа G1 бесконечна, если бесконечна группа G2; в) элемент а 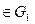 такой, что
такой, что 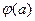 имеет бесконечный порядок, является элементом, имеющим бесконечный порядок.
имеет бесконечный порядок, является элементом, имеющим бесконечный порядок.
10. Докажите, что аддитивная группа Z, аддитивная группа черных чисел и мультипликативная группа целых степеней числа 2 изоморфны между собой.
11. Докажите, что аддитивная группа R изоморфна группе матриц вида 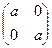 , где
, где 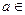 R, относительно матричного сложения.
R, относительно матричного сложения.
12. Докажите, что множество двумерных арифметических векторов ( a, b) и множество матриц вида 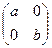 , где
, где 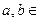 R, являются изоморфными группами относительных операций сложения в этих множествах.
R, являются изоморфными группами относительных операций сложения в этих множествах.
13. Выясните, изоморфна ли группа 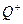 по умножению группе Q по сложению.
по умножению группе Q по сложению.
Указание. Предположим, что существует изоморфное отображение 
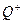 →Q. Пусть
→Q. Пусть 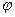 (1) = а. Тогда
(1) = а. Тогда  при любом натуральном n (тем самым а ≠1) и
при любом натуральном n (тем самым а ≠1) и 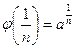 . Значит, число
. Значит, число 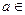 Q должно быть таким, что
Q должно быть таким, что 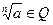 при любом натуральном п. Покажите, что такого числа а ≠1 не существует.
при любом натуральном п. Покажите, что такого числа а ≠1 не существует.
14. Выясните, изоморфна ли группа всех самосовмещений ромба группе всех самосовмещений прямоугольника.
15. Группу самосовмещений правильного треугольника изоморфно отобразите на симметрическую группу S3.
16. Докажите изоморфизм групп 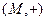 и
и 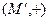 , где
, где 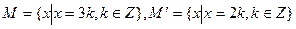 .
.
17. Докажите, что аддитивная группа целых чисел гомоморфна мультипликативной группе ({1, - 1},).
18. Какие из следующих отображений являются изоморфными отображениями указанных алгебр:
а) 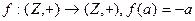 ;
;
б) 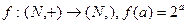 ;
;
в) 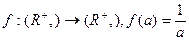 ;
;
г) 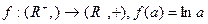 ;
;
д) 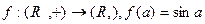 .
.
Дата: 2018-11-18, просмотров: 1288.