Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Вопросы теории

1. Понятие левого и правого смежных классов группы по подгруппе.
2. Левое и правое разложение группы по подгруппе.
3. Нормальный делитель группы.
4. Факторгруппа группы по ее нормальному делителю.
5. Теорема Лагранжа.

Образцы решения задач

 

Задача 1. Найти левое и правое разложение симметрической группы

S3 = } по ее подгруппе . Совпадают ли они между собой?

Решение. а) Найдем левое разложение группы S3 . В качестве первого левого класса можно взять смежный класс элемента е, то есть саму подгруппу 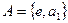. Возьмем любой элемент из S3, не вошедший в первый класс, например элемент а 2 , и умножим его справа на элементы подгруппы 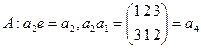. Получим второй смежный класс: 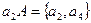. Далее возьмем из группы S3 элемент, который не вошел в два построенных смежных класса, например а 5 . С его помощью получим третий класс: 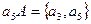. В построенные классы вошли все элементы группы S3, то есть

 S3. Эти классы попарно не пересекаются. Следовательно, классы А, 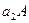,  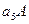составляют искомое левое разложение группы по ее подгруппе А.

б) Найдем правое разложение группы S3 по подгруппе А. Первый правый класс – сама подгруппа 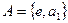, второй правый класс - 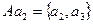. Далее возьмем любой элемент из S3, не вошедший в эти классы, например 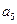, и с его помощью получим третий правый класс: . Так как эти классы не пересекаются и 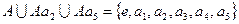= S3, то классы 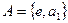, , 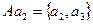 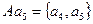составляют правое разложение группы S3 по подгруппе А.

в) Так как 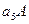, то левое и правое разложения группы S3 по подгруппе А не совпадают.

 

Задача 2. Построить факторгруппу аддитивной группы Z по ее подгруппе В = (5) = 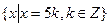. Найти сумму смежных классов 3+В, 4+ В и элемент факторгруппы Z/ B, противоположный элементу 2+В.

Решение. Аддитивная группа Z коммутативна, а потому любая ее подгруппа, в том числе и данная циклическая подгруппа В, является нормальным делителем группы Z. Следовательно, оба разложения группы Z по подгруппе В одинаковы – левые и правые классы соответственно совпадут и из них составится одна определенная факторгруппа. Разбиваем группу Z с помощью ее подгруппы В на попарно непересекающиеся классы. За первый смежный класс берем саму подгруппу В = (5) ={…, -15, -10, -5, 0, 5, 10, 15, …} = 0+B – этот класс состоит из всех тех целых чисел, которые кратны 5; второй смежный класс порождаем с помощью какого-либо целого числа, не вошедшего в первый класс, например с помощью числа 1, непосредственно следующего за 0, путем сложения 1 с элементами подгруппы ={…,-14, -9, -4, 1, 6, 11, 16, ….}. В этот класс войдут, как видим, все те целые числа, которые при делении на 5 дают остаток 1. Третий класс образуем из всех тех целых чисел, которые при делении на 5 дают остаток 2; это будет класс 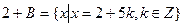. Аналогично четвертый класс 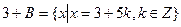; пятый класс 4+ В. А так как при делении целых чисел на 5 остатки могут быть лишь числа 0, 1, 2, 3, 4, то с помощью подгруппы В = (5) никаких других смежных классов, которые были бы отличны от найденных, получить нельзя. Построенные нами смежные классы полностью исчерпывают элементы данной группы Z, то есть 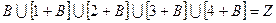. Как легко заметить, полученные классы не имеют общих элементов, то есть попарно не пересекаются. Следовательно, они составляют разбиение множества Z, то есть разложение группы Z по нормальному делителю В. Итак, Z/ B = {B, 1 + B, 2 + B, 3 + B, 4 + B} есть искомая факторгруппа. Она является также аддитивной группой. По правилу сложения элементов в аддитивной факторгруппе имеем: (3+В) + (4+В) = (3+4) + В = 7 + В = 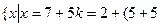k) = 2 + 5t, t 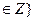= 2 + В;

(3+В) + В = (3+В) + (0 + В) = (3 + 0) + В = 3 + В. Аналогично В + (3 + В) =  3 + В, поэтому элемент В в группе Z/ B является нулевым. Поскольку (2 + B) +(3 + B) = (2 + 3) + В = 5 + В =  = В, элемент 3+В является противоположным для элемента 2 + В.

 

Задачи для решения.

 

1. Найдите все левые смежные классы группы самосовмещений правильного треугольника: а) по подгруппе М поворотов треугольника; б) по подгруппе 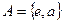, где а – одна из симметрий.

 

2. Известно, что Н – любая подгруппа группы G и х 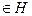. Докажите, что хН = Нх = Н.

 

 

3. Докажите, что если элемент у входит в левый смежный класс хН по Н, порожденный элементом х, то смежный класс уН совпадает со смежным классом хН.

 

4. Аддитивную группу Z гомоморфно отобразите на фактор группу 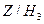, где .

 

5. Постройте левое и правое разложение группы G самосовмещений правильного треугольника: а) по подгруппе М вращений этого треугольника, результаты сравнить; б) по подгруппе 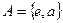, где а – одна из симметрий.

 

6. Постройте левое и правое разложение группы самосовмещений квадрата по подгруппе 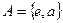, где а – отражение относительно диагонали.

 

 

7. Что представляют собой разложения произвольной группы G по ее единичной подгруппе и по самой G?

 

 

8. Группа содержит 4 элемента, из которых лишь один имеет порядок 4. Какой порядок имеют остальные элементы группы, сколько подгрупп имеет эта группа?

 

 

9. Сколько подгрупп может иметь группа G, содержащая 17 элементов?

 

 

10. Докажите, что если Н – подгруппа группы G, а х – некоторый элемент из G, то множество 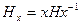является подгруппой G. В группе G самосовмещений квадрата найдите все подгруппы вида 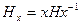, где Н – группа поворотов квадрата.

 

 

11. Докажите, что если порядок подгруппы в 2 раза меньше порядка самой группы, то эта подгруппа является нормальным делителем группы.

 

 

12. Докажите, что подгруппа Н группы G является нормальным делителем тогда и только тогда, когда для любого элемента а из Н и любого элемента g из G элемент 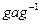содержится в Н.

Примечание. Элемент 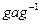называется сопряженным элементу а.

 

13.В группе всех самосовмещений квадрата взята подгруппа Н = 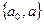, где  - тождественное преобразование, а – отражение относительно одной из диагоналей квадрата. Является ли Н нормальным делителем.

 

14. Найдите все нормальные делители в симметрической группе S3 третьей степени.

 

15. Докажите, что группа 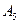 не содержит нормальных делителей, кроме единичной подгруппы и всей группы.

 

 

16. Докажите, что в мультипликативной группе G вещественных невырожденных матриц п-го порядка подмножество Н матриц, определитель которых равен 1, является нормальным делителем. Как можно охарактеризовать смежные классы по Н?

 

 

17. Составьте факторгруппу группы самосовмещений квадрата по ее нормальному делителю А = .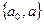

 

 

18. Докажите, что если группа Является циклической с образующей а, то и факторгруппа этой группы по любому ее нормальному делителю Н будет также циклической с образующей аН.

 

 

19. Почему подгруппа А = 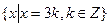аддитивной группы Z является нормальным делителем группы Z? Постройте факторгруппу Z / A. Будет ли она циклической? Если да, то каков будет ее образующий элемент и как ее элементы могут быть записаны через этот образующий элемент?

Примечание. Если число смежных классов (левых или правых) группы G по ее подгруппе Н конечно, то это число называют индексом подгруппы Н (в группе G).

 

20. Постройте факторгруппу Z / A, где А =(6) = 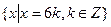. Будет ли она абелевой? Найдите (6 + А) + (9 + А) и (9 + А) + (6 + А).

 

21. Постройте факторгруппу Z / A , где А = (6), В = (4), и составьте для нее таблицу сложения. Найдите элемент, противоположный элементу 5 + М, где М = А .

 

 

22. Будет ли А = 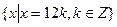=(12) подгруппой, нормальным делителем группы М = 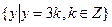= (3)? Ответ обоснуйте. Постройте факторгруппу М / А и таблицу сложения ее элементов.

 

 

23. На множестве G всевозможных троек целых чисел определена бинарная операция 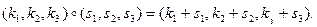Докажите, что система G = является группой и что подгруппа 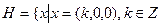является нормальным делителем группы G.

 

 

Тема 6. Кольца.

Вопросы теории

1. Кольцо.
2. Числовые кольца.
3. Виды колец.
4. Делители нуля.
5. Область целостности.

Образцы решения задач

Задача 1. Доказать, что множество М матриц вида 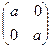, где a – любое действительное число, является кольцом относительно матричного сложения и умножения.

Решение. 1) Рассмотрим сумму и произведение двух матриц 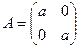,  данного множества: А + В = 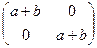, АВ = .

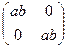Мы видим, что А + В Î М, АВ Î М, то есть множество М замкнуто относительно матричного сложения и умножения.

2) Из теории матриц известно, что на множестве квадратных матриц одного и того же порядка, а значит, и на множество М, сложение коммутативно, сложение и умножение ассоциативны и умножение дистрибутивно относительно сложения.

3) Уравнение 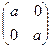+ Х = 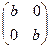 имеет единственное решение Х = 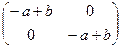, снова принадлежащее множеству М.

Следовательно, множество М является кольцом.

 

 

Задачи для решения.

 

1.Выясните, образует ли кольцо относительно обычных сложения и умножения: а) множество N; б) множество Z; в) множество всех нечетных чисел; г) множество всех четных чисел; д) множество чисел вида 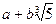, где - любые целые числа. В каких из указанных случаев существует единичный элемент (то есть нейтральный элемент для операции умножения)?

 

2.Является ли кольцом множество L чисел вида 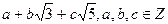, относительно обычных операций сложения и умножения?

 

 

3.Покажите, что множество чисел вида , является числовым кольцом, то есть кольцом относительно обычных операций сложения и умножения над числами.

 

 

4.Докажите, что в любом кольце для любых его элементов 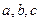 имеют место свойства: а) если a+ b = a+ c, то b= c; б) a- b = a+(- b); в) – ( a+ b) = - a – b; г) – ( a – b) = b – a.

 

 

5.Запишите левый и правый дистрибутивный законы, если операция 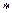 дистрибутивна относительно операции 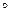. Дистрибутивно ли обычное сложение относительно обычного умножения?

 

 

6.Выясните, дистрибутивна ли операция  относительно операции 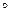, если  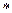является операцией возведения в степень на множестве N, а 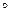- операцией умножения на том же множестве, то есть , где 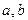- любые элементы из N.

 

 

7.Справедливы ли формулы сокращенного умножения для элементов некоммутативных колец?

 

 

8.Выясните, является ли кольцом относительно матричного сложения и умножения: а) множество всех вещественных матриц одного и того же порядка n > 1; б) множество матриц вида 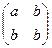 с рациональными компонентами; в) множество вещественных матриц вида .

 

 

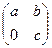9.Докажите, что множество М матриц вида 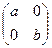 составляет коммутативное кольцо относительно матричного сложения и умножения. Выделите мультипликативную группу этого кольца.

 

10. Какие элементы кольца называют делителями нуля? Выясните, имеет ли кольцо М вещественных матриц вида 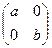 делители нуля 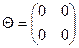этого кольца.

 

 

11. Докажите, что множество А чисел вида 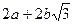 где 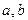- любые целые числа, является числовым кольцом.

 

 

12. Докажите, что множество 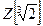 чисел вида 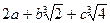, где 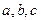- любые целые числа, является числовым кольцом.

 

 

13. Докажите, что если М – коммутативная группа относительно операции сложения, такая, что ab = 0 для любых 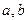 и нулевого элемента 0 группы М, то система М =  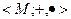является кольцом.

 

 

14. Докажите, что если на Z задана операция , то алгебраическая система

 

<Z; +, Ä> является коммутативным кольцом с единицей. Каков единичный элемент этого кольца?

 

15. На множестве A = Q² упорядоченных пар (a; b) рациональных чисел сложение 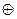и умножение 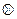определены следующими правилами: .

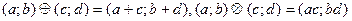Покажите, что является коммутативным кольцом с единицей и с делителями нуля.

 

16. Докажите, что если на множестве 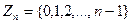, кроме операции сложения 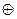по модулю п, определена еще операция умножения Ä по модулю п, состоящая в том , что в качестве результата этой операции над двумя числами из 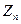берется остаток от деления на п обычного произведения, то система  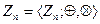является коммутативным кольцом.

Примечание. Это кольцо называется кольцом вычетов по модулю п.

 

17. Составьте таблицы сложения и умножения элементов колец Z 3 и Z 8 , а также выясните, имеются ли в этих кольцах делители нуля.

 

18. Выясните, является ли I – множество подмножеств некоторого непустого множества – кольцом относительно операций объединения 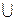 и пересечения .

 

 

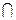19. Выясните, является ли система <Z; 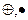> кольцом относительно обычного умножения и операции сложения , выполняемой по правилу:

 

 

 

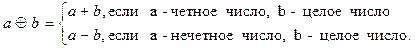
20. Докажите, что множество 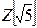 чисел вида 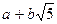, где 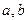- любые целые числа, является числовым кольцом. Разрешимы ли в этом кольце уравнения , , ?

 

 

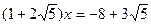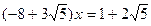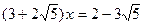Тема 7. Подкольца.

Вопросы теории

1. Подкольцо.

2. Критерий подкольца.

 

Образцы решения задач

Задача 1. Доказать, что множество А четных целых чисел есть подкольцо кольца целых чисел Z.

Решение. Имеем:

1) А = 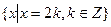, А Ì Z.                                                          (1)

2) Пусть х 1, х 2 – любые элементы из А, то есть х 1 = 2k 1, х 2 = 2k 2, 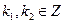. Так как Z есть кольцо, то  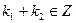и потому

.                                  (2)

3) Пусть х = 2k есть любой элемент из А, следовательно, 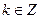; тогда и 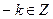, а потому

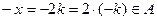.                                                                       (3)

Из (1), (2), (3) следует, что А есть подгруппа аддитивной группы кольца Z.

4) Кроме того, если х 1, х 2 – любые элементы из А, т.е. х 1 = 2k 1, х 2 = 2k 2, 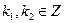, то 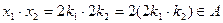, так как  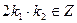(Z кольцо).

Следовательно, А является подкольцом кольца Z.

 

Задачи для решения.

 

1. Докажите, что если непустое подмножество L кольца К содержит сумму и произведение двух любых своих элементов и для всякого своего элемента содержит противоположный ему элемент, то L является подкольцом кольца К.

 

2. Докажите, что если непустое подмножество L кольца К содержит разность и произведение любых своих элементов, то L является подкольцом кольца К.

 

 

3. Охарактеризуйте все подкольца кольца 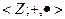 целых чисел.

 

 

4. Докажите, что множество L матриц вида 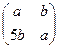, , 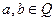является подкольцом кольца М всех вещественных матриц порядка 2.

 

 

5. В кольце М всех вещественных матриц порядка 2 укажите несколько подмножеств, которые являются его подкольцами.

 

 

6. Какой вид имеют все подкольца кольца 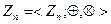 вычетов по модулю п? Сколько их у кольца ?

 

 

7. Докажите, что множество диагональных матриц порядка п ≥2, то есть матриц вида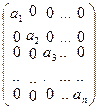  

 

с действительными элементами, является подкольцом кольца М всех вещественных матриц порядка n. Будет ли оно коммутативным? Иметь делители нуля?