Вопросы теории
1. Понятие делимости в кольце.
2. Обратимые элементы кольца.
3. Свойства делимости.
4. Ассоциированные элементы.
5. Простые и составные элементы кольца.
Образцы решения задач
Задача 1. Делится ли число 23+2i на число 2+3i в кольце  ?
?
Решение. В самом деле, 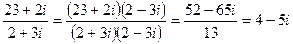 , а 4-5i Î
, а 4-5i Î 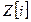 . Следовательно, число 23+2i делится на число 2+3i в кольце
. Следовательно, число 23+2i делится на число 2+3i в кольце 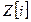 .
.
Задача 2. Покажите, что в кольце 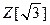 число 13 является составным.
число 13 является составным.
Решение. Число 13 можно представить в виде 13 = (4 - 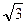 )(4 +
)(4 + 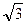 ), (4 -
), (4 - 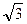 ) и (4 +
) и (4 + 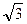 )принадлежат
)принадлежат 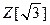 . Докажем, что (4 -
. Докажем, что (4 - 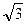 ) и (4 +
) и (4 + 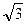 ) необратимы.
) необратимы.
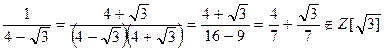 ,
,
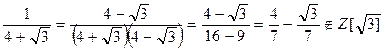 . Так как 13 мы представили в виде произведения необратимых элементов кольца
. Так как 13 мы представили в виде произведения необратимых элементов кольца 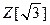 , то 13 в этом кольце является составным числом.
, то 13 в этом кольце является составным числом.
Задачи для решения.
1. Какие элементы кольца называются обратимыми? Найдите обратимые элементы в кольцах 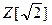 чисел вида
чисел вида 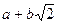 , a, b
, a, b 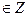 , и
, и 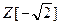 .
.
2. Делится ли число 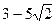 на число
на число 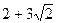 в кольце
в кольце 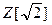 ? А число
? А число 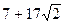 на число
на число 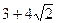 ?
?
3. Какие элементы поля Q рациональных чисел делятся на число 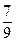 ?
?
4. Делится ли в кольце 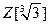 число
число 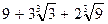 на число
на число 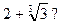
5. Какими дополнительными свойствами обладает отношение делимости в области целостности?
6. Докажите, что если а – делитель нуля в кольце R, то все элементы вида ab, где b  , тоже являются делителями нуля.
, тоже являются делителями нуля.
7. Пусть R – область целостности. Является ли областью целостности 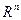 ? (Рассмотрите произведение (а, 0) (0, b).)
? (Рассмотрите произведение (а, 0) (0, b).)
8. Докажите, что элементы 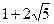 ,
, 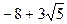 кольца
кольца 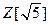 ассоциированы.
ассоциированы.
9. Докажите, что числа 7 и 3 простые в кольце 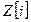 и числа 13 и 17 составные в кольце
и числа 13 и 17 составные в кольце 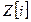 .
.
10. Докажите, что 2 разлагается в кольце 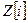 в произведение двух необратимых сомножителей.
в произведение двух необратимых сомножителей.
Тема 10. Идеалы в кольцах.
Вопросы теории
1. Идеал кольца.
2. Свойства идеалов колец.
3. Главные идеалы колец.
4. Свойства главных идеалов.
5. Смежные классы кольца по идеалу.
6. Факторкольцо.
Образцы решения задач.
Задача 1. Проверить является ли кольцо 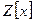 многочленов с целыми коэффициентами идеалом в кольце
многочленов с целыми коэффициентами идеалом в кольце 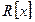 .
.
Например, многочлен 2 + 3х принадлежит 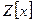 , а кратный ему многочлен
, а кратный ему многочлен  имеет дробные коэффициенты и потому не принадлежит
имеет дробные коэффициенты и потому не принадлежит 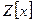 . Следовательно, кольцо
. Следовательно, кольцо 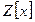 многочленов с целыми коэффициентами идеалом в кольце
многочленов с целыми коэффициентами идеалом в кольце 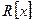 не является.
не является.
Задача 2. Доказать, что множество I многочленов с нулевым свободным членом является идеалом в кольце 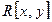 многочленов от двух переменных с действительными коэффициентами.
многочленов от двух переменных с действительными коэффициентами.
Решение. Если свободные члены многочленов 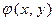 и
и 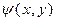 равны нулю, то же самое верно и для многочлена
равны нулю, то же самое верно и для многочлена 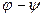 , а также для любого многочлена вида
, а также для любого многочлена вида 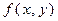 ×
× 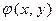 , где
, где 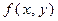
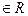 [x, y]. Иными словами, если
[x, y]. Иными словами, если 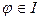 и
и 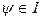 , то
, то 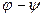
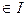 , а если
, а если 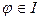 и f
и f  [x, y], то f
[x, y], то f 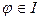 . Значит, I – идеал в кольце
. Значит, I – идеал в кольце 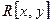 . Этот идеал не является главным. В самом деле, многочлены х и у принадлежат I, но в I нет ни одного многочлена, которому были бы кратны и х и у.
. Этот идеал не является главным. В самом деле, многочлены х и у принадлежат I, но в I нет ни одного многочлена, которому были бы кратны и х и у.
Задачи для решения.
1. Являются ли идеалами:
а) Z в 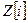 ; и)
; и) 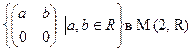 ;
;
б)  в
в 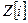 ; к)
; к) 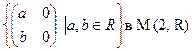 ;
;
в) 3Z в Z; л) 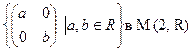 ;
;
г) 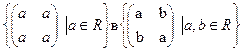 ; м)
; м)  в
в 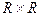 ;
;
д) 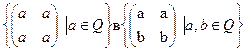 ; н)
; н) 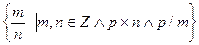 в Qp;
в Qp;
е) 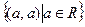 в
в 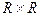 ; о) Z в
; о) Z в  ;
;
ж) 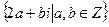 в
в 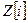 ; п) (п Z) [x] в
; п) (п Z) [x] в  ;
;
з) 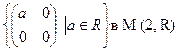 ; р) множество всех многочленов на
; р) множество всех многочленов на 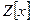 с
с
четным старшим коэффициентом в 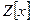 .
.
2. Найдите все идеалы в кольцах Z, 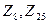 .
.
3. Пусть А - кольцо, J1, J2 – идеалы А. Обозначим 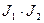 - множество всех элементов из А, которое можно представить в виде
- множество всех элементов из А, которое можно представить в виде  , где
, где 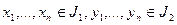 . Докажите, что
. Докажите, что  идеал А и
идеал А и 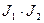 Í
Í 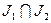 .
.
4. Какие из чисел 3 – 5i, 4 + 6i, - 15 + 9i, 5 – 3i принадлежат идеалу (3 + 5i) кольца целых гауссовых чисел? Какие из них порождают этот идеал?
5. Найдите идеал (2) в Z; в 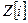 ; в
; в  ; в Q[x].
; в Q[x].
6. Укажите, какие включения имеют место для следующих идеалов кольца целых чисел: 3Z, 2Z, 4Z, 5Z, 6Z, (-11)Z, 24Z, (-4)Z, 13Z, 33Z, 12Z. Нарисуйте граф и сравните его с графом отношения делимости на множестве {2, 3, 4, 5, 6, 11, 12, 13, 24, 33}.
7. Сколько элементов в факторкольце Z/6Z? Составьте таблицы сложения и умножения для элементов этого факторкольца.
8. Укажите числа, принадлежащие одному смежному классу по идеалу (2) в кольце 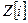 : - 3 + 5i; 7 – 8i; 25 + 3i; 47 + 10i; -2; 1 + i; 1 – i; 3i; 1; -1; 2 +i; -2 + 3i.
: - 3 + 5i; 7 – 8i; 25 + 3i; 47 + 10i; -2; 1 + i; 1 – i; 3i; 1; -1; 2 +i; -2 + 3i.
9. Найдите все элементы факторкольца 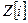 /(2). Составьте таблицы сложения и умножения. Покажите, что это факторкольцо не является областью целостности.
/(2). Составьте таблицы сложения и умножения. Покажите, что это факторкольцо не является областью целостности.
10. Какие из следующих равенств имеют место в факторкольце 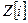 /(3):
/(3):
а) 1 + 2i + (3) = 1 - 2i + (3); г) 3i + (3) = 0 + (3);
б) 1 + (3) = i + (3); д) 3 – i + (3) = 3 +i + (3)?
в) 3i + (3) = 3 + (3);
11. Укажите все элементы кольца 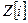 /(3), составьте таблицы сложения и умножения.
/(3), составьте таблицы сложения и умножения.
12. Сколько элементов содержит факторкольцо 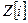 /(5)?
/(5)?
13. Среди следующих элементов факторкольца R[ x]/( x² + x + 1) укажите равные нулю:
а) 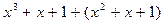 ; в)
; в) 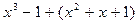 ;
;
б) 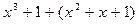 ; г)
; г) 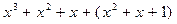 .
.
Тема 11. Поля.
Вопросы теории
- Поле.
- Подполе.
- Характеристика поля.
- Изоморфизм полей.
Задача 1. Доказать, что множество М матриц вида 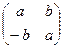 , где a и b – любые действительные числа, является полем относительно матричного сложения и умножения. Найти характеристику этого поля.
, где a и b – любые действительные числа, является полем относительно матричного сложения и умножения. Найти характеристику этого поля.
Решение. 1) Рассмотрим сумму и произведение двух матриц 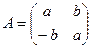 ,
, 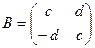 данного множества: А + В =
данного множества: А + В = 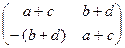 , АВ =
, АВ =  .
.
Мы видим, что А + В Î М, АВ Î М, то есть множество М замкнуто относительно матричного сложения и умножения.
2) Из теории матриц известно, что на множестве квадратных матриц одного и того же порядка, а значит, и на множестве М, сложение коммутативно, сложение и умножение ассоциативны и умножение дистрибутивно относительно сложения.
3) Уравнение 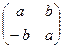 + Х =
+ Х = 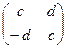 имеет единственное решение
имеет единственное решение
Х = 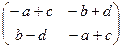 , снова принадлежащее множеству М.
, снова принадлежащее множеству М.
4) ВА = 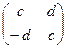
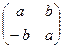 =
= 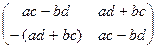 = АВ, то есть умножение в М коммутативно.
= АВ, то есть умножение в М коммутативно.
5) Рассмотрим уравнение АХ = В, где 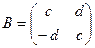 ,
, 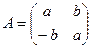 ≠
≠ 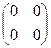 и, следовательно, а ≠ 0 или b ≠ 0. Тогда çА ç= a² + b² ≠ 0, то есть матрица А является невырожденной, а значит, она имеет обратную матрицу
и, следовательно, а ≠ 0 или b ≠ 0. Тогда çА ç= a² + b² ≠ 0, то есть матрица А является невырожденной, а значит, она имеет обратную матрицу 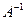 . В таком случае уравнение
. В таком случае уравнение
АХ = В имеет единственное решение Х = 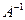 В. Докажем, что это решение принадлежит данному множеству М. Имеем:
В. Докажем, что это решение принадлежит данному множеству М. Имеем:
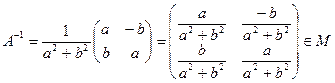 .
.
Из того, что 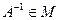 , В Î М, имеем в силу первой части доказательства Х =
, В Î М, имеем в силу первой части доказательства Х = 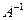 В Î М. Итак, рассматриваемое уравнение в М разрешимо и имеет единственное решение. Из результатов, найденных в пунктах 1 – 5, следует по определению поля, что М есть поле.
В Î М. Итак, рассматриваемое уравнение в М разрешимо и имеет единственное решение. Из результатов, найденных в пунктах 1 – 5, следует по определению поля, что М есть поле.
Найдем характеристику поля М. Нулем поля М является матрица 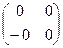 =
= 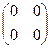 . Единицей поля М является матрица
. Единицей поля М является матрица 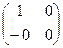 =
= 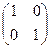 = Е. По правилу умножения числа на матрицу получим, что при любом натуральном п п
= Е. По правилу умножения числа на матрицу получим, что при любом натуральном п п 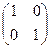 =
= 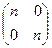 ≠
≠ 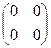 , то есть не существует натурального п такого, чтобы п
, то есть не существует натурального п такого, чтобы п 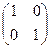 =
= 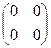 . А это значит, что характеристика поля М равна нулю.
. А это значит, что характеристика поля М равна нулю.
Задачи для решения.
1. Докажите, что алгебраическая система – множество Q рациональных чисел с обычной операцией сложения и операцией 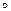 , выполняемой по правилу
, выполняемой по правилу 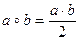 для любых элементов из Q, - является полем. Каков единичный элемент этого поля?
для любых элементов из Q, - является полем. Каков единичный элемент этого поля?
2. Докажите, что если коммутативное кольцо К состоит из конечного числа п элементов, где п > 1, и не содержит делителей нуля, то оно является полем.
Указание. Пусть а – отличный от нуля элемент из К. Покажите, что отображение х →ах является взаимно однозначным отображением К на себя. Выведите отсюда разрешимость уравнения ах = b.
3. Докажите, что множество матриц вида 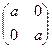 , где а – любое рациональное (или действительное) число, является полем относительно матричного сложения и умножения. Будет ли множество матриц данного вида составлять поле, если а – любое целое число?
, где а – любое рациональное (или действительное) число, является полем относительно матричного сложения и умножения. Будет ли множество матриц данного вида составлять поле, если а – любое целое число?
4. Почему кольцо {0} не является полем?
5. На множестве М = {a, b} сложение 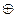 и умножение
и умножение  определены следующим образом:
определены следующим образом:
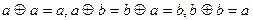 ;
;
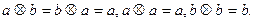
Выясните, обладает ли это множество нулем и единицей и является ли система <M; 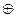 ,
, 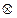 > полем относительно заданных бинарных операций.
> полем относительно заданных бинарных операций.
6. Докажите, что если В – множество пар (а; b) рациональных чисел и на В две бинарные операции - сложение 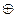 и умножение
и умножение 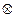 - определены следующим условиями:
- определены следующим условиями:
 , то система В = <B;
, то система В = <B; 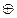 ,
,  > является полем, а пары (0; 0) и (1; 0) соответственно нулем и единицей этого поля.
> является полем, а пары (0; 0) и (1; 0) соответственно нулем и единицей этого поля.
7. Докажите, что кольцо 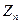 вычетов по модулю п не является полем, если п – составное число.
вычетов по модулю п не является полем, если п – составное число.
8. Убедитесь в том, что поле А = {0, 1} с обычной операцией умножения и операцией сложения  , задаваемой равенствами 1
, задаваемой равенствами 1  1=0
1=0 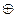 0=0, 1
0=0, 1 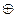 0=0
0=0 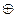 1=1, имеет характеристику, равную двум.
1=1, имеет характеристику, равную двум.
9. Приведите примеры полей, характеристика которых равна нулю.
10. Докажите, что не существует полей характеристикой которых была бы единица или какое-либо составное натуральное число.
11. Докажите, что если непустое подмножество L любого поля Р содержит сумму и произведение двух любых своих элементов, а также для любого своего элемента содержит противоположный ему элемент и для любого своего ненулевого элемента содержит обратный ему элемент, то L является подполем поля Р.
12. В поле матриц вида 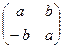 , где а, b
, где а, b 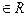 , укажите такие его подмножества, которые являются подполями.
, укажите такие его подмножества, которые являются подполями.
13. Докажите, что множество В = 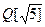 чисел вида
чисел вида 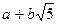 , где a, b – любые рациональные числа, является числовым полем.
, где a, b – любые рациональные числа, является числовым полем.
14. Докажите, что область целостности R, состоящая из конечного числа элементов, является полем.
15. Решите систему уравнений
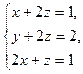
над полями: а) 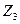 ; б)
; б) 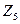 ; в)
; в) 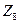 .
.
16. Докажите, что в поле М = 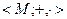 , где М – множество всех матриц вида
, где М – множество всех матриц вида 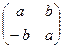 с действительными а и b, а +,
с действительными а и b, а +,  являются операциями над матрицами, существует элемент Х, такой, что Х² = - Е (Е – единица поля М).
являются операциями над матрицами, существует элемент Х, такой, что Х² = - Е (Е – единица поля М).
17. Докажите, что изоморфны поле матриц вида 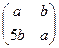 и поле упорядоченных пар (а; b), в котором сложение
и поле упорядоченных пар (а; b), в котором сложение  и умножение
и умножение  определены по следующим правилам:
определены по следующим правилам:
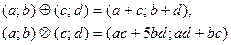 где a, b – любые рациональные числа.
где a, b – любые рациональные числа.
18. Покажите, что любое поле из двух элементов изоморфно полю 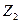 .
.
19. Докажите, что пересечение любой совокупности подполей поля F есть подполе поля F.
Дата: 2018-11-18, просмотров: 1118.