Группы. Кольца. Поля.
Методические указания и материалы для практических занятий по алгебре со студентами специальности 010100 - Математика
Курган 2011
Кафедра алгебры, геометрии и методики преподавания математики
Дисциплина: «Алгебра» (специальность 010100 - Математика)
Составитель: доцент Шатных О.Н.
Утверждены на заседании кафедры «__»____________2011г.
Рекомендованы методическим
советом университета
содержание
Введение ………………………………………………………………….......4
Тема 1. Бинарная алгебраическая операция …………………………….....5
Тема 2. Группы ………………………………………………………….........9
Тема 3. Подгруппы……………………………. ………………………….....12
Тема 4. Изоморфизмы и гомоморфизмы групп…………………………….13
Тема 5.Смежные классы по подгруппе……………………………………...15
Тема 6.Кольца…………………………………………………………………19
Тема 7. Подкольца…………………………………………………………….21
Тема 8. Гомоморфизмы и изоморфизмы колец……………………………..23
Тема 9. Делимость в кольцах………………………………………………....24
Тема 10. Идеалы колец………………………………………………………..25
Тема 11. Поля………………………………………………………………….27
Тема 12. Упорядоченные поля……………………………………………….29
Тема 13. Алгебраические числа………. ………………………………….....31
Тема 14. Расширения полей…………………….. ………………………......34
Литература ……………………………………………………………..…. …38
введение
Настоящее пособие составлено в соответствии с программой дисциплины «Алгебра» и предназначено для студентов направления «Математика». Кроме того, пособие будет полезно студентам направления «Педагогическое образование» профиля «Математическое образование», которые также изучают данный раздел алгебры, но в несколько меньшем объеме.
Раздел «Алгебраические системы» изучается в третьем семестре. В данном пособии представлены все темы раздела, которые выносятся на практические занятия. Для каждой темы указаны вопросы для повторения теоретического материала, приведены образцы решения типовых задач и список задач для решения.
Тема 2. Группы.
Вопросы теории
- Определение группы. Примеры.
- Виды групп.
- Подстановки.
- Симметрическая группа подстановок n-й степени.
Образцы решения задач
Задача 1. Доказать, что множество Z образует группу относительно действия, заданного формулой
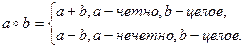 .
.
Доказательство. 1. Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а поскольку как сложение, так и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.
2. Проанализируем возможные случаи:
а) Если a, b – четные числа, а с – любое число из Z, то
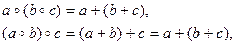
то есть 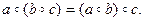
б) Если a – четное число, b – нечетное число, а с – любое число из Z, то
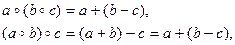
то есть 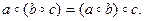
в) Если a – нечетное число, b – четное число, а с – любое число из Z, то a – b нечетно и потому
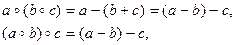
то есть 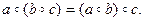
г) Если a, b – нечетные числа, а с – любое число из Z, то a – b четно и потому

то есть 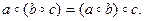
Итак, во всех возможных случаях заданная на Z бинарная операция является ассоциативной.
3. Так как 0 – четное число, то 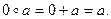 Кроме того, если а четно, то
Кроме того, если а четно, то 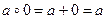 ; если же а нечетно, то
; если же а нечетно, то 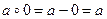 . Итак,
. Итак, 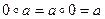 , то есть 0 является в Z нейтральным элементом относительно заданной операции.
, то есть 0 является в Z нейтральным элементом относительно заданной операции.
4. Для любого элемента а 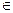 Z в Z существует обратный элемент: для четного а обратным будет противоположное число – а, так как
Z в Z существует обратный элемент: для четного а обратным будет противоположное число – а, так как 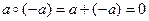 ; для нечетного а обратным будет само число а, так как
; для нечетного а обратным будет само число а, так как 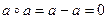
Итак, Z является группой относительно заданной операции.
Однако эта группа не является абелевой, поскольку 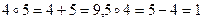 , то есть
, то есть 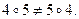
Задачи для решения.
1. Выясните, какие из нижеприведенных множеств являются группами относительно нижеуказанных операций:
а) множество Z относительно вычитания;
б) множество четных чисел относительно умножения;
в) множество целых чисел, кратных любому заданному натуральному числу n, относительно сложения;
г) множество  относительно умножения;
относительно умножения;
д) множество Q относительно умножения;
е) множество Q \ {0} относительно умножения;
ж) множество R \ {0} относительно умножения;
з) множество квадратных матриц n-го порядка относительно сложения, умножения;
и) множество матриц n-го порядка с определителем, равным 1, относительно умножения матриц, сложения;
к) множество решений любой заданной системы линейных однородных уравнений относительно сложения;
л) множество трехмерных (n-мерных) арифметических векторов относительно сложения;
м) множество чисел вида 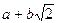 относительно сложения, если a и b – любые рациональные числа;
относительно сложения, если a и b – любые рациональные числа;
н) множество параллельных переносов в плоскости относительно операции их последовательного выполнения;
о) множество многочленов одной и той же степени n от одного аргумента относительно сложения;
п) множество многочленов степени не выше n относительно сложения;
р) множество многочленов от одного аргумента относительно сложения;
с) множество матриц вида 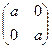 , где
, где  R относительно сложения матриц;
R относительно сложения матриц;
т) множество матриц вида 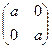 , где
, где  R, а ≠ 0, относительно сложения матриц.
R, а ≠ 0, относительно сложения матриц.
2. Докажите, что множество матриц вида 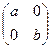 , где a и b –действительные, отличные от нуля числа, составляют группу относительно матричного умножения.
, где a и b –действительные, отличные от нуля числа, составляют группу относительно матричного умножения.
3. Докажите, что множество матриц вида 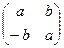 , где a и b – любые, не равные одновременно нулю действительные числа, образует группу относительно матричного умножения.
, где a и b – любые, не равные одновременно нулю действительные числа, образует группу относительно матричного умножения.
4. Докажите, что множество матриц вида 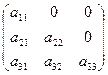 , где a ii ≠ 0 (I = 1, 2, 3), является группой относительно матричного умножения.
, где a ii ≠ 0 (I = 1, 2, 3), является группой относительно матричного умножения.
5. Составьте таблицу умножения элементов симметрической группы S3 подстановок 3-й степени, обозначив элементы этой группы буквами. По таблице найдите взаимно обратные элементы этой группы и докажите, что рассматриваемая группа не является коммутативной.
6. Для множества G 1 = 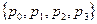 , состоящего из подстановок
, состоящего из подстановок 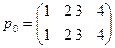 ,
, 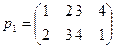 ,
, 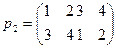 ,
, 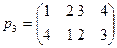 , составьте таблицу умножения и с ее помощью убедитесь, что G 1 – абелева группа.
, составьте таблицу умножения и с ее помощью убедитесь, что G 1 – абелева группа.
7. Дано множество М = 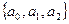 поворотов (вращений) правильного треугольника в плоскости этого треугольника вокруг его центра против часовой стрелки соответственно на углы 0º, 120º, 240º. Эти повороты совмещают треугольник с самим собой. Последовательное выполнение двух любых таких поворотов называется произведением (композицией) этих двух поворотов. Докажите, что М является группой относительно введенной в М операции.
поворотов (вращений) правильного треугольника в плоскости этого треугольника вокруг его центра против часовой стрелки соответственно на углы 0º, 120º, 240º. Эти повороты совмещают треугольник с самим собой. Последовательное выполнение двух любых таких поворотов называется произведением (композицией) этих двух поворотов. Докажите, что М является группой относительно введенной в М операции.
8. На множестве Q \ {0} определено действие 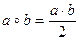 . Докажите, что относительно указанного действия данное множество является группой.
. Докажите, что относительно указанного действия данное множество является группой.
9.Пусть G – множество всевозможных троек чисел вида  и
и 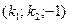 и пусть на G определено действие, выполняемое по правилу
и пусть на G определено действие, выполняемое по правилу 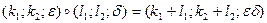 . Докажите, что относительно указанного действия G является группой.
. Докажите, что относительно указанного действия G является группой.
Тема 3. Подгруппы.
Вопросы теории
- Определение подгруппы.
- Циклическая подгруппа. Циклическая группа.
- Образующий циклической группы.
- Порядок элемента группы.
- Порядок группы.
Образцы решения задач
Задача 1. Доказать, что множество А целых чисел, кратных трем, есть подгруппа аддитивной группы Z.
Решение. Имеем:
1) А = 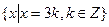 , А Ì Z. (1)
, А Ì Z. (1)
2) Пусть х 1, х 2 – любые элементы из А, то есть х 1 = 3k 1, х 2 = 3k 2, 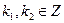 . Так как Z есть аддитивная группа, то
. Так как Z есть аддитивная группа, то 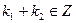 и потому
и потому
 . (2)
. (2)
3) Пусть х = 3k есть любой элемент из А, следовательно, 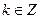 ; тогда и
; тогда и 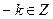 , а потому
, а потому
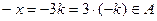 . (3)
. (3)
Из (1), (2), (3) следует, что А есть подгруппа аддитивной группы Z.
Задачи для решения.
1. Докажите, что множество четных чисел является подгруппой аддитивной группы Z целых чисел. Является ли множество нечетных чисел подгруппой группы Z?
2. Пусть п – заданное натуральное число. Показать, что множество целых чисел, кратных п, является подгруппой аддитивной группы Z.
3. Докажите, что множество целых степеней 3 является подгруппой мультипликативной группы Q \ {0}. Запишите эту подгруппу символически. Является ли она циклической? Каков порядок элемента, порождающего эту подгруппу?
4. Найдите порядки элементов  ,
, 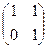 ,
, 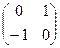 мультипликативной группы невырожденных матриц второго порядка.
мультипликативной группы невырожденных матриц второго порядка.
5. Найдите порядок каждого элемента симметрической группы S3 третьей степени, а затем выясните, какие циклические подгруппы S3 они порождают. Сколько всего различных подгрупп имеет группа S3? Является ли А3 циклической подгруппой группы S3? Каковы ее образующие? (А3 – знакопеременная группа третьей степени.)
6. Найдите порядок элемента а = (1243) 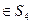 и постройте циклическую подгруппу группы
и постройте циклическую подгруппу группы 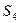 , порожденную элементом а.
, порожденную элементом а.
7. Сколько подгрупп имеет группа 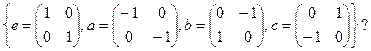
8. Элементы группы G всех самосовмещений квадрата представьте подстановками четвертой степени. Составьте для группы G таблицу Кэли. Изоморфно отобразите группу G на одну из подгрупп симметрической группы S8 восьмой степени.
9. Докажите, что симметрическая группа 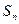 при любом натуральном п ≥ 5 содержит подгруппу, изоморфную знакопеременной группе
при любом натуральном п ≥ 5 содержит подгруппу, изоморфную знакопеременной группе 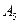 .
.
Тема 6. Кольца.
Вопросы теории
- Кольцо.
- Числовые кольца.
- Виды колец.
- Делители нуля.
- Область целостности.
Образцы решения задач
Задача 1. Доказать, что множество М матриц вида 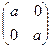 , где a – любое действительное число, является кольцом относительно матричного сложения и умножения.
, где a – любое действительное число, является кольцом относительно матричного сложения и умножения.
Решение. 1) Рассмотрим сумму и произведение двух матриц 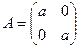 ,
,  данного множества: А + В =
данного множества: А + В = 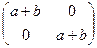 , АВ =
, АВ = 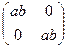 .
.
Мы видим, что А + В Î М, АВ Î М, то есть множество М замкнуто относительно матричного сложения и умножения.
2) Из теории матриц известно, что на множестве квадратных матриц одного и того же порядка, а значит, и на множество М, сложение коммутативно, сложение и умножение ассоциативны и умножение дистрибутивно относительно сложения.
3) Уравнение 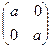 + Х =
+ Х = 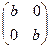 имеет единственное решение Х =
имеет единственное решение Х = 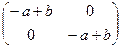 , снова принадлежащее множеству М.
, снова принадлежащее множеству М.
Следовательно, множество М является кольцом.
Задачи для решения.
1.Выясните, образует ли кольцо относительно обычных сложения и умножения: а) множество N; б) множество Z; в) множество всех нечетных чисел; г) множество всех четных чисел; д) множество чисел вида 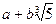 , где
, где  - любые целые числа. В каких из указанных случаев существует единичный элемент (то есть нейтральный элемент для операции умножения)?
- любые целые числа. В каких из указанных случаев существует единичный элемент (то есть нейтральный элемент для операции умножения)?
2.Является ли кольцом множество L чисел вида 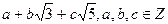 , относительно обычных операций сложения и умножения?
, относительно обычных операций сложения и умножения?
3.Покажите, что множество чисел вида  , является числовым кольцом, то есть кольцом относительно обычных операций сложения и умножения над числами.
, является числовым кольцом, то есть кольцом относительно обычных операций сложения и умножения над числами.
4.Докажите, что в любом кольце для любых его элементов 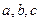 имеют место свойства: а) если a+ b = a+ c, то b= c; б) a- b = a+(- b); в) – ( a+ b) = - a – b; г) – ( a – b) = b – a.
имеют место свойства: а) если a+ b = a+ c, то b= c; б) a- b = a+(- b); в) – ( a+ b) = - a – b; г) – ( a – b) = b – a.
5.Запишите левый и правый дистрибутивный законы, если операция 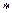 дистрибутивна относительно операции
дистрибутивна относительно операции 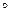 . Дистрибутивно ли обычное сложение относительно обычного умножения?
. Дистрибутивно ли обычное сложение относительно обычного умножения?
6.Выясните, дистрибутивна ли операция  относительно операции
относительно операции 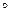 , если
, если 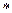 является операцией возведения в степень на множестве N, а
является операцией возведения в степень на множестве N, а 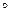 - операцией умножения на том же множестве, то есть
- операцией умножения на том же множестве, то есть  , где
, где 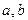 - любые элементы из N.
- любые элементы из N.
7.Справедливы ли формулы сокращенного умножения для элементов некоммутативных колец?
8.Выясните, является ли кольцом относительно матричного сложения и умножения: а) множество всех вещественных матриц одного и того же порядка n > 1; б) множество матриц вида 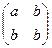 с рациональными компонентами; в) множество вещественных матриц вида
с рациональными компонентами; в) множество вещественных матриц вида 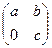 .
.
9.Докажите, что множество М матриц вида 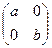 составляет коммутативное кольцо относительно матричного сложения и умножения. Выделите мультипликативную группу этого кольца.
составляет коммутативное кольцо относительно матричного сложения и умножения. Выделите мультипликативную группу этого кольца.
10. Какие элементы кольца называют делителями нуля? Выясните, имеет ли кольцо М вещественных матриц вида 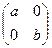 делители нуля
делители нуля 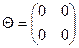 этого кольца.
этого кольца.
11. Докажите, что множество А чисел вида 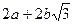 где
где 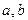 - любые целые числа, является числовым кольцом.
- любые целые числа, является числовым кольцом.
12. Докажите, что множество 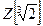 чисел вида
чисел вида 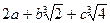 , где
, где 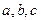 - любые целые числа, является числовым кольцом.
- любые целые числа, является числовым кольцом.
13. Докажите, что если М – коммутативная группа относительно операции сложения, такая, что ab = 0 для любых 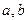 и нулевого элемента 0 группы М, то система М =
и нулевого элемента 0 группы М, то система М = 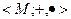 является кольцом.
является кольцом.
14. Докажите, что если на Z задана операция  , то алгебраическая система
, то алгебраическая система
<Z; +, Ä> является коммутативным кольцом с единицей. Каков единичный элемент этого кольца?
15. На множестве A = Q² упорядоченных пар (a; b) рациональных чисел сложение 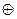 и умножение
и умножение 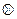 определены следующими правилами:
определены следующими правилами: 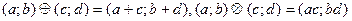 .
.
Покажите, что  является коммутативным кольцом с единицей и с делителями нуля.
является коммутативным кольцом с единицей и с делителями нуля.
16. Докажите, что если на множестве 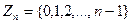 , кроме операции сложения
, кроме операции сложения 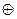 по модулю п, определена еще операция умножения Ä по модулю п, состоящая в том , что в качестве результата этой операции над двумя числами из
по модулю п, определена еще операция умножения Ä по модулю п, состоящая в том , что в качестве результата этой операции над двумя числами из 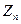 берется остаток от деления на п обычного произведения, то система
берется остаток от деления на п обычного произведения, то система 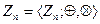 является коммутативным кольцом.
является коммутативным кольцом.
Примечание. Это кольцо называется кольцом вычетов по модулю п.
17. Составьте таблицы сложения и умножения элементов колец Z 3 и Z 8 , а также выясните, имеются ли в этих кольцах делители нуля.
18. Выясните, является ли I – множество подмножеств некоторого непустого множества – кольцом относительно операций объединения 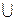 и пересечения
и пересечения 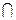 .
.
19. Выясните, является ли система <Z; 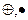 > кольцом относительно обычного умножения и операции сложения
> кольцом относительно обычного умножения и операции сложения 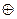 , выполняемой по правилу:
, выполняемой по правилу:
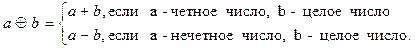
20. Докажите, что множество 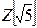 чисел вида
чисел вида 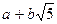 , где
, где 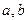 - любые целые числа, является числовым кольцом. Разрешимы ли в этом кольце уравнения
- любые целые числа, является числовым кольцом. Разрешимы ли в этом кольце уравнения 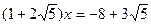 ,
, 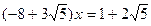 ,
, 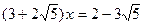 ?
?
Тема 7. Подкольца.
Вопросы теории
1. Подкольцо.
2. Критерий подкольца.
Образцы решения задач
Задача 1. Доказать, что множество А четных целых чисел есть подкольцо кольца целых чисел Z.
Решение. Имеем:
1) А = 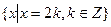 , А Ì Z. (1)
, А Ì Z. (1)
2) Пусть х 1, х 2 – любые элементы из А, то есть х 1 = 2k 1, х 2 = 2k 2, 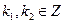 . Так как Z есть кольцо, то
. Так как Z есть кольцо, то 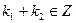 и потому
и потому
 . (2)
. (2)
3) Пусть х = 2k есть любой элемент из А, следовательно, 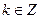 ; тогда и
; тогда и 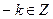 , а потому
, а потому
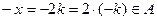 . (3)
. (3)
Из (1), (2), (3) следует, что А есть подгруппа аддитивной группы кольца Z.
4) Кроме того, если х 1, х 2 – любые элементы из А, т.е. х 1 = 2k 1, х 2 = 2k 2, 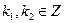 , то
, то 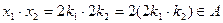 , так как
, так как 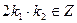 (Z кольцо).
(Z кольцо).
Следовательно, А является подкольцом кольца Z.
Задачи для решения.
1. Докажите, что если непустое подмножество L кольца К содержит сумму и произведение двух любых своих элементов и для всякого своего элемента содержит противоположный ему элемент, то L является подкольцом кольца К.
2. Докажите, что если непустое подмножество L кольца К содержит разность и произведение любых своих элементов, то L является подкольцом кольца К.
3. Охарактеризуйте все подкольца кольца 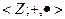 целых чисел.
целых чисел.
4. Докажите, что множество L матриц вида 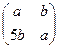 ,
, 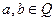 , является подкольцом кольца М всех вещественных матриц порядка 2.
, является подкольцом кольца М всех вещественных матриц порядка 2.
5. В кольце М всех вещественных матриц порядка 2 укажите несколько подмножеств, которые являются его подкольцами.
6. Какой вид имеют все подкольца кольца 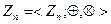 вычетов по модулю п? Сколько их у кольца
вычетов по модулю п? Сколько их у кольца  ?
?
7. Докажите, что множество диагональных матриц порядка п ≥2, то есть матриц вида 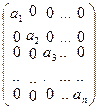
с действительными элементами, является подкольцом кольца М всех вещественных матриц порядка n. Будет ли оно коммутативным? Иметь делители нуля?
Тема 10. Идеалы в кольцах.
Вопросы теории
1. Идеал кольца.
2. Свойства идеалов колец.
3. Главные идеалы колец.
4. Свойства главных идеалов.
5. Смежные классы кольца по идеалу.
6. Факторкольцо.
Образцы решения задач.
Задача 1. Проверить является ли кольцо 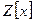 многочленов с целыми коэффициентами идеалом в кольце
многочленов с целыми коэффициентами идеалом в кольце 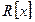 .
.
Например, многочлен 2 + 3х принадлежит 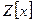 , а кратный ему многочлен
, а кратный ему многочлен  имеет дробные коэффициенты и потому не принадлежит
имеет дробные коэффициенты и потому не принадлежит 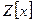 . Следовательно, кольцо
. Следовательно, кольцо 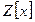 многочленов с целыми коэффициентами идеалом в кольце
многочленов с целыми коэффициентами идеалом в кольце 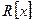 не является.
не является.
Задача 2. Доказать, что множество I многочленов с нулевым свободным членом является идеалом в кольце 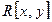 многочленов от двух переменных с действительными коэффициентами.
многочленов от двух переменных с действительными коэффициентами.
Решение. Если свободные члены многочленов 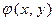 и
и 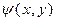 равны нулю, то же самое верно и для многочлена
равны нулю, то же самое верно и для многочлена 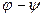 , а также для любого многочлена вида
, а также для любого многочлена вида 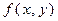 ×
× 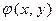 , где
, где 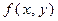
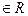 [x, y]. Иными словами, если
[x, y]. Иными словами, если 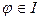 и
и 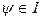 , то
, то 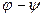
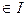 , а если
, а если 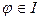 и f
и f  [x, y], то f
[x, y], то f 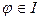 . Значит, I – идеал в кольце
. Значит, I – идеал в кольце 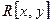 . Этот идеал не является главным. В самом деле, многочлены х и у принадлежат I, но в I нет ни одного многочлена, которому были бы кратны и х и у.
. Этот идеал не является главным. В самом деле, многочлены х и у принадлежат I, но в I нет ни одного многочлена, которому были бы кратны и х и у.
Задачи для решения.
1. Являются ли идеалами:
а) Z в 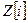 ; и)
; и) 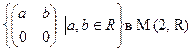 ;
;
б)  в
в 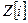 ; к)
; к) 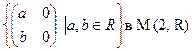 ;
;
в) 3Z в Z; л) 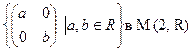 ;
;
г) 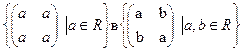 ; м)
; м)  в
в 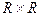 ;
;
д) 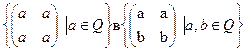 ; н)
; н) 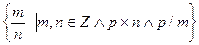 в Qp;
в Qp;
е) 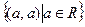 в
в 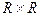 ; о) Z в
; о) Z в  ;
;
ж) 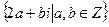 в
в 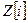 ; п) (п Z) [x] в
; п) (п Z) [x] в  ;
;
з) 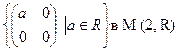 ; р) множество всех многочленов на
; р) множество всех многочленов на 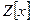 с
с
четным старшим коэффициентом в 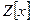 .
.
2. Найдите все идеалы в кольцах Z, 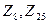 .
.
3. Пусть А - кольцо, J1, J2 – идеалы А. Обозначим 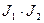 - множество всех элементов из А, которое можно представить в виде
- множество всех элементов из А, которое можно представить в виде  , где
, где 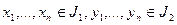 . Докажите, что
. Докажите, что  идеал А и
идеал А и 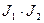 Í
Í 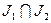 .
.
4. Какие из чисел 3 – 5i, 4 + 6i, - 15 + 9i, 5 – 3i принадлежат идеалу (3 + 5i) кольца целых гауссовых чисел? Какие из них порождают этот идеал?
5. Найдите идеал (2) в Z; в 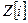 ; в
; в  ; в Q[x].
; в Q[x].
6. Укажите, какие включения имеют место для следующих идеалов кольца целых чисел: 3Z, 2Z, 4Z, 5Z, 6Z, (-11)Z, 24Z, (-4)Z, 13Z, 33Z, 12Z. Нарисуйте граф и сравните его с графом отношения делимости на множестве {2, 3, 4, 5, 6, 11, 12, 13, 24, 33}.
7. Сколько элементов в факторкольце Z/6Z? Составьте таблицы сложения и умножения для элементов этого факторкольца.
8. Укажите числа, принадлежащие одному смежному классу по идеалу (2) в кольце 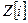 : - 3 + 5i; 7 – 8i; 25 + 3i; 47 + 10i; -2; 1 + i; 1 – i; 3i; 1; -1; 2 +i; -2 + 3i.
: - 3 + 5i; 7 – 8i; 25 + 3i; 47 + 10i; -2; 1 + i; 1 – i; 3i; 1; -1; 2 +i; -2 + 3i.
9. Найдите все элементы факторкольца 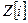 /(2). Составьте таблицы сложения и умножения. Покажите, что это факторкольцо не является областью целостности.
/(2). Составьте таблицы сложения и умножения. Покажите, что это факторкольцо не является областью целостности.
10. Какие из следующих равенств имеют место в факторкольце 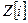 /(3):
/(3):
а) 1 + 2i + (3) = 1 - 2i + (3); г) 3i + (3) = 0 + (3);
б) 1 + (3) = i + (3); д) 3 – i + (3) = 3 +i + (3)?
в) 3i + (3) = 3 + (3);
11. Укажите все элементы кольца 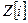 /(3), составьте таблицы сложения и умножения.
/(3), составьте таблицы сложения и умножения.
12. Сколько элементов содержит факторкольцо 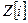 /(5)?
/(5)?
13. Среди следующих элементов факторкольца R[ x]/( x² + x + 1) укажите равные нулю:
а) 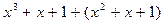 ; в)
; в) 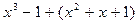 ;
;
б) 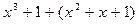 ; г)
; г) 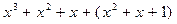 .
.
Тема 11. Поля.
Вопросы теории
- Поле.
- Подполе.
- Характеристика поля.
- Изоморфизм полей.
Задача 1. Доказать, что множество М матриц вида 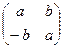 , где a и b – любые действительные числа, является полем относительно матричного сложения и умножения. Найти характеристику этого поля.
, где a и b – любые действительные числа, является полем относительно матричного сложения и умножения. Найти характеристику этого поля.
Решение. 1) Рассмотрим сумму и произведение двух матриц 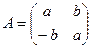 ,
, 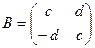 данного множества: А + В =
данного множества: А + В = 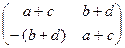 , АВ =
, АВ =  .
.
Мы видим, что А + В Î М, АВ Î М, то есть множество М замкнуто относительно матричного сложения и умножения.
2) Из теории матриц известно, что на множестве квадратных матриц одного и того же порядка, а значит, и на множестве М, сложение коммутативно, сложение и умножение ассоциативны и умножение дистрибутивно относительно сложения.
3) Уравнение 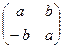 + Х =
+ Х = 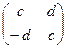 имеет единственное решение
имеет единственное решение
Х = 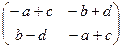 , снова принадлежащее множеству М.
, снова принадлежащее множеству М.
4) ВА = 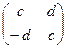
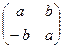 =
= 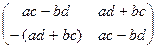 = АВ, то есть умножение в М коммутативно.
= АВ, то есть умножение в М коммутативно.
5) Рассмотрим уравнение АХ = В, где 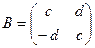 ,
, 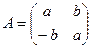 ≠
≠ 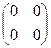 и, следовательно, а ≠ 0 или b ≠ 0. Тогда çА ç= a² + b² ≠ 0, то есть матрица А является невырожденной, а значит, она имеет обратную матрицу
и, следовательно, а ≠ 0 или b ≠ 0. Тогда çА ç= a² + b² ≠ 0, то есть матрица А является невырожденной, а значит, она имеет обратную матрицу 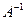 . В таком случае уравнение
. В таком случае уравнение
АХ = В имеет единственное решение Х = 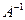 В. Докажем, что это решение принадлежит данному множеству М. Имеем:
В. Докажем, что это решение принадлежит данному множеству М. Имеем:
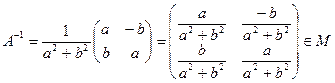 .
.
Из того, что  , В Î М, имеем в силу первой части доказательства Х =
, В Î М, имеем в силу первой части доказательства Х =  В Î М. Итак, рассматриваемое уравнение в М разрешимо и имеет единственное решение. Из результатов, найденных в пунктах 1 – 5, следует по определению поля, что М есть поле.
В Î М. Итак, рассматриваемое уравнение в М разрешимо и имеет единственное решение. Из результатов, найденных в пунктах 1 – 5, следует по определению поля, что М есть поле.
Найдем характеристику поля М. Нулем поля М является матрица 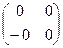 =
= 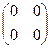 . Единицей поля М является матрица
. Единицей поля М является матрица 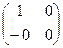 =
= 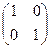 = Е. По правилу умножения числа на матрицу получим, что при любом натуральном п п
= Е. По правилу умножения числа на матрицу получим, что при любом натуральном п п 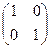 =
= 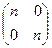 ≠
≠ 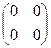 , то есть не существует натурального п такого, чтобы п
, то есть не существует натурального п такого, чтобы п 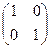 =
= 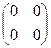 . А это значит, что характеристика поля М равна нулю.
. А это значит, что характеристика поля М равна нулю.
Задачи для решения.
1. Докажите, что алгебраическая система – множество Q рациональных чисел с обычной операцией сложения и операцией  , выполняемой по правилу
, выполняемой по правилу 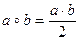 для любых элементов из Q, - является полем. Каков единичный элемент этого поля?
для любых элементов из Q, - является полем. Каков единичный элемент этого поля?
2. Докажите, что если коммутативное кольцо К состоит из конечного числа п элементов, где п > 1, и не содержит делителей нуля, то оно является полем.
Указание. Пусть а – отличный от нуля элемент из К. Покажите, что отображение х →ах является взаимно однозначным отображением К на себя. Выведите отсюда разрешимость уравнения ах = b.
3. Докажите, что множество матриц вида 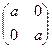 , где а – любое рациональное (или действительное) число, является полем относительно матричного сложения и умножения. Будет ли множество матриц данного вида составлять поле, если а – любое целое число?
, где а – любое рациональное (или действительное) число, является полем относительно матричного сложения и умножения. Будет ли множество матриц данного вида составлять поле, если а – любое целое число?
4. Почему кольцо {0} не является полем?
5. На множестве М = {a, b} сложение 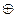 и умножение
и умножение  определены следующим образом:
определены следующим образом:
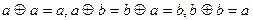 ;
;
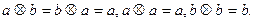
Выясните, обладает ли это множество нулем и единицей и является ли система <M; 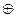 ,
, 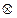 > полем относительно заданных бинарных операций.
> полем относительно заданных бинарных операций.
6. Докажите, что если В – множество пар (а; b) рациональных чисел и на В две бинарные операции - сложение 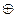 и умножение
и умножение 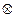 - определены следующим условиями:
- определены следующим условиями:
 , то система В = <B;
, то система В = <B; 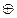 ,
, 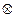 > является полем, а пары (0; 0) и (1; 0) соответственно нулем и единицей этого поля.
> является полем, а пары (0; 0) и (1; 0) соответственно нулем и единицей этого поля.
7. Докажите, что кольцо 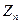 вычетов по модулю п не является полем, если п – составное число.
вычетов по модулю п не является полем, если п – составное число.
8. Убедитесь в том, что поле А = {0, 1} с обычной операцией умножения и операцией сложения 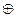 , задаваемой равенствами 1
, задаваемой равенствами 1 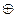 1=0
1=0 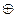 0=0, 1
0=0, 1 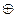 0=0
0=0 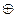 1=1, имеет характеристику, равную двум.
1=1, имеет характеристику, равную двум.
9. Приведите примеры полей, характеристика которых равна нулю.
10. Докажите, что не существует полей характеристикой которых была бы единица или какое-либо составное натуральное число.
11. Докажите, что если непустое подмножество L любого поля Р содержит сумму и произведение двух любых своих элементов, а также для любого своего элемента содержит противоположный ему элемент и для любого своего ненулевого элемента содержит обратный ему элемент, то L является подполем поля Р.
12. В поле матриц вида 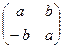 , где а, b
, где а, b 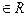 , укажите такие его подмножества, которые являются подполями.
, укажите такие его подмножества, которые являются подполями.
13. Докажите, что множество В = 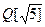 чисел вида
чисел вида 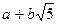 , где a, b – любые рациональные числа, является числовым полем.
, где a, b – любые рациональные числа, является числовым полем.
14. Докажите, что область целостности R, состоящая из конечного числа элементов, является полем.
15. Решите систему уравнений
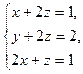
над полями: а) 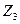 ; б)
; б) 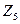 ; в)
; в) 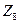 .
.
16. Докажите, что в поле М = 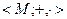 , где М – множество всех матриц вида
, где М – множество всех матриц вида 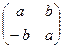 с действительными а и b, а +,
с действительными а и b, а +, 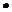 являются операциями над матрицами, существует элемент Х, такой, что Х² = - Е (Е – единица поля М).
являются операциями над матрицами, существует элемент Х, такой, что Х² = - Е (Е – единица поля М).
17. Докажите, что изоморфны поле матриц вида 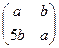 и поле упорядоченных пар (а; b), в котором сложение
и поле упорядоченных пар (а; b), в котором сложение 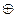 и умножение
и умножение  определены по следующим правилам:
определены по следующим правилам:
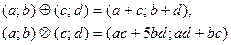 где a, b – любые рациональные числа.
где a, b – любые рациональные числа.
18. Покажите, что любое поле из двух элементов изоморфно полю 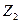 .
.
19. Докажите, что пересечение любой совокупности подполей поля F есть подполе поля F.
Тема 14. Расширения полей.
Вопросы теории
1. Расширение поля.
2. Простое алгебраическое расширение поля.
3. Составное алгебраическое расширение поля.
4. Размерность расширения.
Образцы решения задач
Задача 1. Поле Q последовательно расширяется – сначала с помощью числа 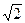 , затем с помощью
, затем с помощью 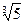 : Q Ì Q1 Ì Q2, где Q1 = Q(
: Q Ì Q1 Ì Q2, где Q1 = Q( 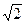 ),Q2 = Q1 (
),Q2 = Q1 ( 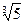 ).
).
Доказать, что такое расширение может быть достигнуто в один шаг – с помощью числа 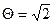 +
+ 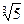 , то есть что Q(
, то есть что Q( 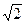 )(
)( 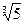 )=Q(
)=Q( 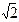 +
+ 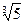 ).
).
Решение. Согласно теореме о простоте составного расширения любые два последовательно произведенных простых алгебраических расширения поля Р

( 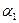 алгебраично над Р, а
алгебраично над Р, а 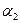 - над Р1) могут быть заменены одним, то есть существует такое число
- над Р1) могут быть заменены одним, то есть существует такое число 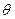 , алгебраическое над Р, что
, алгебраическое над Р, что
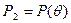 .
.
Наша задача – показать, что в случае, когда Р есть поле Q рациональных чисел, а 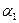 =
= 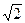 и
и 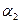 =
= 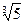 , в качестве
, в качестве  можно взять
можно взять 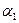 +
+ 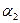 .
.
Достаточно показать, что поле Q ( 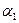 +
+ 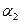 ) содержит каждое из чисел
) содержит каждое из чисел 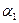 и
и 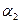 , так как в этом случае оно будет содержать поле Q1 = Q(
, так как в этом случае оно будет содержать поле Q1 = Q(  ) и число
) и число 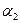 , а значит, и поле Q2 = Q1(
, а значит, и поле Q2 = Q1( 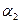 ); тогда из Q (
); тогда из Q ( 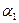 +
+ 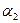 ) É Q2 и Q (
) É Q2 и Q ( 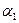 +
+ 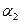 )Ì Q2 (второе включение является очевидным) будет следовать: Q (
)Ì Q2 (второе включение является очевидным) будет следовать: Q ( 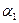 +
+ 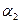 ) = Q2.
) = Q2.
На самом деле достаточно показать еще меньше – что поле Q ( 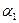 +
+ 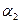 ) содержит
) содержит 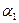 , так как
, так как 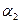 тогда будет принадлежать полю Q (
тогда будет принадлежать полю Q (  +
+ 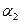 ) как разность двух чисел из этого поля (
) как разность двух чисел из этого поля ( 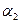 = (
= ( 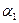 +
+ 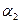 ) -
) - 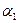 ).
).
Для сокращения записей обозначим поле Q ( 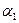 +
+ 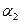 ) через L. Допустим, рассуждая от противного, что число
) через L. Допустим, рассуждая от противного, что число 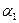 =
= 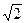 не принадлежит L. Рассмотрим два многочлена над L:
не принадлежит L. Рассмотрим два многочлена над L:
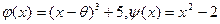
(напомним, что 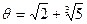 ). Каждый из них имеет одним из своих корней число
). Каждый из них имеет одним из своих корней число 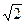 :
:
 ;
; 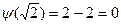 .
.
Проверим, что других общих корней многочлены 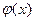 и
и  не имеют.
не имеют.
Действительно, корни 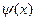 - это числа
- это числа 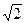 , -
, - 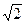 .
.
Корнями же многочлена 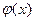 являются корни уравнения
являются корни уравнения 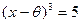 , то есть числа
, то есть числа
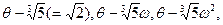
где 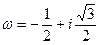 - корень кубический из 1. Следовательно, мы должны проверить, что ни одно из чисел
- корень кубический из 1. Следовательно, мы должны проверить, что ни одно из чисел 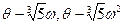 не равно -
не равно - 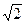 . Но это очевидно, так как числа
. Но это очевидно, так как числа 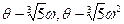 не являются действительными (коэффициент при i отличен от нуля).
не являются действительными (коэффициент при i отличен от нуля).
Поскольку, таким образом, единственный общий корень многочленов 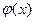 и
и 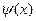 в поле С есть
в поле С есть 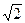 , то (нормированный) наибольший общий делитель многочленов
, то (нормированный) наибольший общий делитель многочленов  и
и 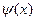 в кольце С [x] есть
в кольце С [x] есть
D (х) = х - 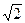 .
.
Этот же самый многочлен должен быть (нормированным) НОД многочленов 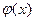 и
и 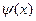 также и в кольце L [x]. Следовательно, все коэффициенты этого многочлена, в частности
также и в кольце L [x]. Следовательно, все коэффициенты этого многочлена, в частности
- 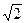 , принадлежат полю L. Тем самым и число
, принадлежат полю L. Тем самым и число 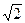 принадлежат L, что и требовалось показать.
принадлежат L, что и требовалось показать.
Задача 2. Найти выражение числа 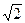 в виде
в виде  , где
, где 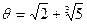 , а f (x), g (x) Î Z [x].
, а f (x), g (x) Î Z [x].
Решение. Сам факт принадлежности числа 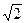 полю Q (
полю Q (  ) был установлен в задаче 1. Наша цель теперь – найти «явное» выражение числа
) был установлен в задаче 1. Наша цель теперь – найти «явное» выражение числа 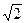 через
через  .
.
Рассмотрим снова многочлены  и
и 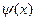 из (1). При решении задачи 1 мы показали, что нормированный НОД этих многочленов есть
из (1). При решении задачи 1 мы показали, что нормированный НОД этих многочленов есть
D (х) = х - 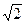 .
.
С другой стороны, НОД можно найти, применяя к  и
и  алгоритм Евклида. Для этого делим сначала
алгоритм Евклида. Для этого делим сначала  на
на 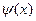 (с остатком):
(с остатком):
__ 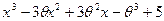 çх² - 2
çх² - 2
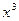 - 2х çх -
- 2х çх - 
___________________________________________________
__ 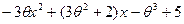
 + 60
+ 60
____________________________________________________________
( 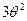 +2)х – (
+2)х – ( 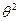 +60 – 5)
+60 – 5)
Мы получили в остатке многочлен
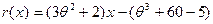
1-й степени. Поскольку ранее уже было доказано, что НОД имеет степень 1, то многочлен 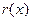 и должен быть как раз НОД многочленов
и должен быть как раз НОД многочленов  и
и 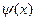 . Следовательно, многочлены
. Следовательно, многочлены
D (х) и 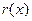 ассоциированы (отличаются лишь численным множителем):
ассоциированы (отличаются лишь численным множителем):
D (х) = 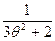
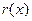 ,
,
или 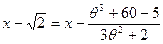 .
.
Отсюда имеем: 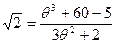 ,
,
что и дает искомое выражение для числа 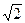 .
.
Задача 3. Пусть Q Ì Q1 Ì Q2, где Q1 = Q( 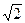 ),Q2 = Q1 (
),Q2 = Q1 ( 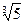 ). Найти степень поля Q2 относительно Q (то есть размерность Q2 над Q).
). Найти степень поля Q2 относительно Q (то есть размерность Q2 над Q).
Решение. Справедлива теорема: если поле Р 1 – конечное расширение поля Р, а поле Р 2 - конечное расширение Р 1, то
 (1)
(1)
В нашем случае, очевидно,  . Покажем, что
. Покажем, что
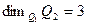 . (2)
. (2)
Чтобы доказать равенство (2), достаточно проверить, что многочлен 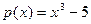 3-й степени, имеющий число
3-й степени, имеющий число 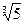 своим корнем, неприводим над Q1. Предположим, что это неверно, то есть что
своим корнем, неприводим над Q1. Предположим, что это неверно, то есть что 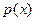 приводим. Тогда один из неприводимых множителей многочлена
приводим. Тогда один из неприводимых множителей многочлена 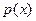 должен быть первой степени, и, следовательно, один из корней многочлена
должен быть первой степени, и, следовательно, один из корней многочлена 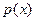 должен принадлежать Q. Таким корнем является, конечно, действительное значение
должен принадлежать Q. Таким корнем является, конечно, действительное значение 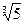 (так как все числа из Q1 действительны). Но число
(так как все числа из Q1 действительны). Но число 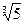 не может принадлежать Q1, так как его степень над Q равна 3, в то время как степень любого числа из Q1 (над полем Q) не выше 2. Полученное противоречие доказывает (2).
не может принадлежать Q1, так как его степень над Q равна 3, в то время как степень любого числа из Q1 (над полем Q) не выше 2. Полученное противоречие доказывает (2).
На основании формулы (1) можем теперь записать:
 . (3)
. (3)
Замечание. Сопоставив (3) с тем фактом, что  , мы можем вывести заключение, что степень числа
, мы можем вывести заключение, что степень числа 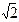 +
+ 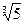 над полем Q равна 6. Это означает, что многочлен 6-й степени (над полем Q), имеющий своим корнем число
над полем Q равна 6. Это означает, что многочлен 6-й степени (над полем Q), имеющий своим корнем число 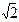 +
+ 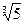 , неприводим.
, неприводим.
Задачи для решения.
1. Пусть p и q – натуральные числа, причем  и
и 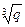 - не целые. Доказать, что
- не целые. Доказать, что
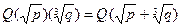 .
.
2. Найти выражение для каждого из чисел 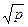 и
и 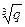 через
через 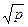 +
+ 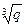 :
:
а) р = 3, q = 6; б) р = 7, q = 4; в) р = 3, q = 3.
3. Пусть p и q – натуральные числа, причем отношение чисел 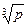 и
и 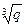 (действительных значений) не является рациональным числом. Доказать, что
(действительных значений) не является рациональным числом. Доказать, что 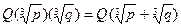 .
.
4. Используя условие задачи 3, найти выражение для каждого из чисел 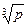 и
и 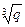 через
через 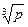 +
+ 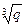 :
:
а) р = 3, q = 7; б) р = 5, q = 12.
Литература
1. Кострикин А. И. Введение в алгебру. В 3-х книгах. Кн. 3: Основные структуры алгебры. – М.: МЦНМО, 2009.
2. Курош А.Г. Курс высшей алгебры. 17-е издание, СПб.- Издательский Дом «Лань».
3. Окунев Л.Я. Высшая алгебра. 3-е издание. СПб.- Издательский Дом «Лань», 2009. 336с.
4. Окунев Л.Я. Сборник задач по высшей алгебре. 2-е издание. СПб.- Издательский Дом «Лань» 2009.
5. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. 17-е издание. СПб. - Издательский Дом «Лань» 288 с.
Группы. Кольца. Поля.
Методические указания и материалы для практических занятий по алгебре со студентами специальности 010100 - Математика
Курган 2011
Кафедра алгебры, геометрии и методики преподавания математики
Дисциплина: «Алгебра» (специальность 010100 - Математика)
Составитель: доцент Шатных О.Н.
Утверждены на заседании кафедры «__»____________2011г.
Рекомендованы методическим
советом университета
содержание
Введение ………………………………………………………………….......4
Тема 1. Бинарная алгебраическая операция …………………………….....5
Тема 2. Группы ………………………………………………………….........9
Тема 3. Подгруппы……………………………. ………………………….....12
Тема 4. Изоморфизмы и гомоморфизмы групп…………………………….13
Тема 5.Смежные классы по подгруппе……………………………………...15
Тема 6.Кольца…………………………………………………………………19
Тема 7. Подкольца…………………………………………………………….21
Тема 8. Гомоморфизмы и изоморфизмы колец……………………………..23
Тема 9. Делимость в кольцах………………………………………………....24
Тема 10. Идеалы колец………………………………………………………..25
Тема 11. Поля………………………………………………………………….27
Тема 12. Упорядоченные поля……………………………………………….29
Тема 13. Алгебраические числа………. ………………………………….....31
Тема 14. Расширения полей…………………….. ………………………......34
Литература ……………………………………………………………..…. …38
введение
Настоящее пособие составлено в соответствии с программой дисциплины «Алгебра» и предназначено для студентов направления «Математика». Кроме того, пособие будет полезно студентам направления «Педагогическое образование» профиля «Математическое образование», которые также изучают данный раздел алгебры, но в несколько меньшем объеме.
Раздел «Алгебраические системы» изучается в третьем семестре. В данном пособии представлены все темы раздела, которые выносятся на практические занятия. Для каждой темы указаны вопросы для повторения теоретического материала, приведены образцы решения типовых задач и список задач для решения.
Тема 1. Бинарная алгебраическая операция. Свойства бинарной алгебраической операции.
Вопросы теории
- Бинарная алгебраическая операция на множестве. Примеры.
- N-арная операция на множестве. Примеры.
- Свойства бинарной алгебраической операции.
- Нейтральный элемент относительно операции.
- Симметричный к данному элемент относительно бинарной алгебраической операции.
- Понятие обратимой операции.
- Алгебраическая система.
- Полугруппа, виды полугрупп.
Образцы решения задач
Задача 1. Покажем, что во множестве М невырожденных матриц n-го порядка  матричное сложение не является бинарной операцией, а матричное умножение – бинарная операция.
матричное сложение не является бинарной операцией, а матричное умножение – бинарная операция.
Решение. а) Для доказательства первого утверждения достаточно привести пример двух таких невырожденных матриц, сумма которых является вырожденной матрицей. Возьмем, например, матрицы
 и
и 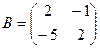 .
.
Поскольку
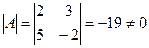 и
и  ,
,
то матрицы А и В являются невырожденными. Сумма же их – матрица С = А + В = 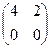 уже не принадлежит множеству невырожденных матриц, поскольку
уже не принадлежит множеству невырожденных матриц, поскольку
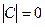 .
.
б) Пусть А и В – любые невырожденные матрицы n-го порядка:
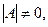
 (1)
(1)
Матрица 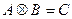 есть снова матрица n-го порядка. Нам остается лишь доказать, что матрица С является невырожденной.
есть снова матрица n-го порядка. Нам остается лишь доказать, что матрица С является невырожденной.
Поскольку, как известно, определитель произведения двух матриц равен произведению определителей этих матриц, то есть
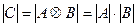 ,
,
то с учетом (1) получаем, что 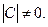 Итак, матрица
Итак, матрица 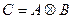 является невырожденной, то есть является элементом того же множества, что и матрицы А и В. По определению бинарной операции умножение во множестве невырожденных матриц n-го порядка является бинарной операцией, а само множество невырожденных матриц с операцией умножения, то есть <M; Ä>, является алгебраической системой.
является невырожденной, то есть является элементом того же множества, что и матрицы А и В. По определению бинарной операции умножение во множестве невырожденных матриц n-го порядка является бинарной операцией, а само множество невырожденных матриц с операцией умножения, то есть <M; Ä>, является алгебраической системой.
Задача 2. Докажите, что на множестве R бинарная операция, заданная формулой 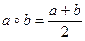 , коммутативна, но не ассоциативна. Выясните, является ли R полугруппой относительно бинарной операции нахождения среднего арифметического?
, коммутативна, но не ассоциативна. Выясните, является ли R полугруппой относительно бинарной операции нахождения среднего арифметического?
Решение. Пусть a, b, с – действительные числа. В силу коммутативности сложения на R получим:
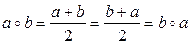 ,
,
то есть бинарная операция нахождения среднего арифметического на R коммутативна.
Далее,
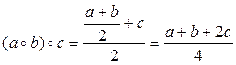 (1)
(1)
и
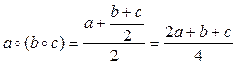 (2)
(2)
Из результатов (1) и (2) следует, что при а ≠ с равенство 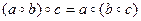 не является справедливым. Следовательно, заданная операция не ассоциативна на R. В силу вышедоказанного R не является полугруппой относительно бинарной операции нахождения среднего арифметического.
не является справедливым. Следовательно, заданная операция не ассоциативна на R. В силу вышедоказанного R не является полугруппой относительно бинарной операции нахождения среднего арифметического.
Задача 3. Докажем, что во множестве К, содержащем не менее двух элементов, на котором формулой 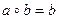 задана бинарная операция, не существует нейтрального элемента.
задана бинарная операция, не существует нейтрального элемента.
Решение. Допустим, что в К существует нейтральный элемент е, и пусть а – любой элемент из К. По определению нейтрального элемента  , а из условия примера следует, что
, а из условия примера следует, что 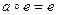 , то есть а = е. Это означает, что К состоит из одного элемента. Полученный результат противоречит условию, а потому сделанное допущение ошибочно.
, то есть а = е. Это означает, что К состоит из одного элемента. Полученный результат противоречит условию, а потому сделанное допущение ошибочно.
Задача 4. Докажите, что на множестве М матриц вида 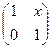 , где х – любое действительное число, бинарная операция матричного умножения обратима.
, где х – любое действительное число, бинарная операция матричного умножения обратима.
Решение. Известно, что на множестве квадратных матриц одного и того же порядка операция матричного умножения ассоциативна. Следовательно, рассматриваемая операция ассоциативна на множестве М.
Пусть  - любая матрица из М. По правилу умножения матриц получим:
- любая матрица из М. По правилу умножения матриц получим:
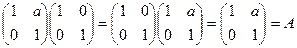 , и потому матрица
, и потому матрица  есть нейтральный элемент. Итак, М обладает нейтральным элементом.
есть нейтральный элемент. Итак, М обладает нейтральным элементом.
Так как  , то матрица
, то матрица  является невырожденной, и, следовательно, она имеет обратную матрицу. Применяя один из способов нахождения обратных матриц, найдем, что
является невырожденной, и, следовательно, она имеет обратную матрицу. Применяя один из способов нахождения обратных матриц, найдем, что 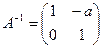 , - а Î R, а потому
, - а Î R, а потому  .
.
Итак, для любого элемента из М во множестве М существует обратный элемент.
Полученные результаты позволяют сделать вывод, что операция матричного умножения обратима на множестве М.
Задачи для решения.
1.Какие из арифметических действий (сложение, вычитание, умножение, деление) являются бинарными операциями:
а) на множестве 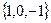 ;
;
б) на множестве N;
в) на множестве Z?
2. Является ли вычитание бинарной операцией на множестве 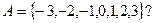
3. Является ли бинарной операцией:
а) умножение на множестве иррациональных чисел;
б) сложение на множестве четных чисел;
в) сложение на множестве нечетных чисел;
г) нахождение десятичных логарифмов на множестве 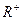 ;
;
д) нахождение среднего геометрического двух чисел на множестве 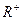 ;
;
е) нахождение наибольшего общего делителя на множестве N?
4.Является ли бинарной операцией матричное умножение на множестве:
а) матриц вида 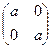 , где а – любое действительное число;
, где а – любое действительное число;
б) треугольных матриц третьего порядка, то есть матриц вида  , где а ij – любые действительные числа?
, где а ij – любые действительные числа?
5. Является ли алгебраической системой множество чисел вида 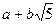 ,
, 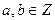 , относительно: а) сложения; б) вычитания; в) умножения?
, относительно: а) сложения; б) вычитания; в) умножения?
6. Докажите, что на множестве 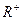 бинарная операция
бинарная операция 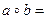
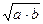 нахождения среднего геометрического коммутативна, но не ассоциативна.
нахождения среднего геометрического коммутативна, но не ассоциативна.
7. Почему действие, выполняемое по правилу 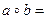
 , не является бинарной операцией на множестве N и является таковой на множестве Z? Выясните, коммутативна ли указанная операция на Z; покажите также, что она не является ассоциативной на этом множестве.
, не является бинарной операцией на множестве N и является таковой на множестве Z? Выясните, коммутативна ли указанная операция на Z; покажите также, что она не является ассоциативной на этом множестве.
8. Покажите, что действие, выполняемое по правилу 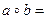
 , является коммутативной, но не ассоциативной бинарной операцией на множестве R.
, является коммутативной, но не ассоциативной бинарной операцией на множестве R.
9. Покажите, что на некотором множестве бинарная операция, заданная формулой 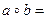
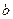 , некоммутативна, но ассоциативна.
, некоммутативна, но ассоциативна.
10. Является ли множество Z полугруппой относительно: а) сложения; б) вычитания?
11. Является ли множество N полугруппой относительно операции нахождения наибольшего общего делителя?
12. Покажите, что множество 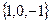 образует полугруппу относительно обычной операции умножения.
образует полугруппу относительно обычной операции умножения.
13. Покажите, что множество четырехмерных арифметических векторов вида
(a, b, b, 0), где 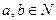 , образует полугруппу относительно операции сложения арифметических векторов.
, образует полугруппу относительно операции сложения арифметических векторов.
14. Пусть I – множество, состоящее из всех подмножеств данного множества М. Покажите, что I образует полугруппу относительно операции пересечения подмножеств.
15. Почему множество R не является полугруппой относительно действия, выполняемого по правилу 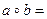
 для любых
для любых 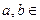 R?
R?
16. Обладает ли множество чисел вида 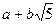 , где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов
, где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов  и
и 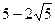 . Обратима ли на данном множестве операция умножения?
. Обратима ли на данном множестве операция умножения?
17. Докажите, что бинарная операция матричного умножения на множестве матриц вида 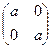 , где а – любое не равное нулю действительное число, обратима. Найдите обратные элементы для матриц
, где а – любое не равное нулю действительное число, обратима. Найдите обратные элементы для матриц 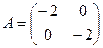 ,
,  ,
, 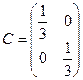 .
.
18. Докажите, что относительно бинарной операции 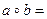
 , множество
, множество 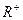 не обладает нейтральным элементом. Обратима ли эта операция на множестве
не обладает нейтральным элементом. Обратима ли эта операция на множестве 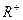 ?
?
19. Пусть I – множество подмножеств некоторого непустого множества М. Существует ли в I нейтральный элемент (если существует, то какой) относительно операции объединения подмножеств на I; пересечения подмножеств? Какие элементы из множества I имеют обратные? Обратимы ли указанные операции на множестве I?
20. Докажите, что на множестве Z действие, выполняемое по правилу 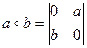 , является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система
, является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система 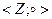 нейтральным элементом, и если обладает, то каким именно?
нейтральным элементом, и если обладает, то каким именно?
21. Докажите, что на множестве Q действие, выполняемое по правилу 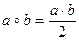 , является бинарной операцией, которая коммутативна, ассоциативна, но не обратима. Каким нейтральным элементом обладает алгебраическая система
, является бинарной операцией, которая коммутативна, ассоциативна, но не обратима. Каким нейтральным элементом обладает алгебраическая система 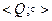 ? Для элемента а = 8 найдите обратный.
? Для элемента а = 8 найдите обратный.
22. Являются ли действия, выполняемые по формулам:
а) 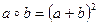 ; д)
; д) 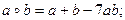
б) 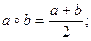 е)
е) 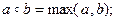
в) 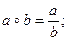 ж)
ж) 
г) 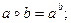 з)
з) 
бинарными операциями на Q, N на множестве вещественных чисел, и если являются, то почему?
23. Какие из нижеприведенных бинарных операций:
а) 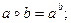
б) 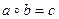 , с – наибольший общий делитель чисел a и b;
, с – наибольший общий делитель чисел a и b;
в) 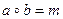 , где m – наименьшее общее кратное чисел a и b
, где m – наименьшее общее кратное чисел a и b
коммутативны, ассоциативны на N?
24. Выясните, какими свойствами обладают операции:
а)  на R/{0};
на R/{0};
б) 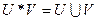 на совокупности подмножеств вещественных чисел;
на совокупности подмножеств вещественных чисел;
в) 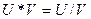 в совокупности подмножеств вещественных чисел;
в совокупности подмножеств вещественных чисел;
г) 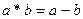 на R;
на R;
д) операция * в множестве учеников класса определяется так, если a и b – два ученика, то a* b – тот из них, кто первым записан на странице классного журнала (если a = b, то a* b = а = b).
25. Покажите, что действие, выполняемое по правилу 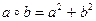 , является коммутативной, но не ассоциативной бинарной операцией на R.
, является коммутативной, но не ассоциативной бинарной операцией на R.
26. Для следующих операций, определенных на множестве 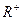 , докажите:
, докажите:
а) операция a* b = ab – ba дистрибутивна относительно сложения; умножения;
б) a* b = 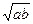 дистрибутивна относительно операции умножения.
дистрибутивна относительно операции умножения.
27. Докажите, что относительно бинарной операции 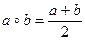 множество R не содержит нейтрального элемента.
множество R не содержит нейтрального элемента.
Тема 2. Группы.
Вопросы теории
- Определение группы. Примеры.
- Виды групп.
- Подстановки.
- Симметрическая группа подстановок n-й степени.
Образцы решения задач
Задача 1. Доказать, что множество Z образует группу относительно действия, заданного формулой
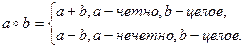 .
.
Доказательство. 1. Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а поскольку как сложение, так и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.
2. Проанализируем возможные случаи:
а) Если a, b – четные числа, а с – любое число из Z, то
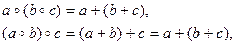
то есть 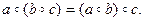
б) Если a – четное число, b – нечетное число, а с – любое число из Z, то
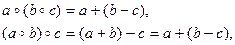
то есть 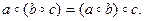
в) Если a – нечетное число, b – четное число, а с – любое число из Z, то a – b нечетно и потому
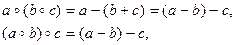
то есть 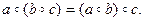
г) Если a, b – нечетные числа, а с – любое число из Z, то a – b четно и потому

то есть 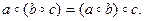
Итак, во всех возможных случаях заданная на Z бинарная операция является ассоциативной.
3. Так как 0 – четное число, то 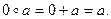 Кроме того, если а четно, то
Кроме того, если а четно, то 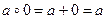 ; если же а нечетно, то
; если же а нечетно, то 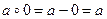 . Итак,
. Итак, 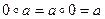 , то есть 0 является в Z нейтральным элементом относительно заданной операции.
, то есть 0 является в Z нейтральным элементом относительно заданной операции.
4. Для любого элемента а 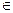 Z в Z существует обратный элемент: для четного а обратным будет противоположное число – а, так как
Z в Z существует обратный элемент: для четного а обратным будет противоположное число – а, так как 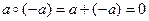 ; для нечетного а обратным будет само число а, так как
; для нечетного а обратным будет само число а, так как 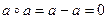
Итак, Z является группой относительно заданной операции.
Однако эта группа не является абелевой, поскольку 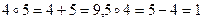 , то есть
, то есть 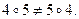
Задачи для решения.
1. Выясните, какие из нижеприведенных множеств являются группами относительно нижеуказанных операций:
а) множество Z относительно вычитания;
б) множество четных чисел относительно умножения;
в) множество целых чисел, кратных любому заданному натуральному числу n, относительно сложения;
г) множество  относительно умножения;
относительно умножения;
д) множество Q относительно умножения;
е) множество Q \ {0} относительно умножения;
ж) множество R \ {0} относительно умножения;
з) множество квадратных матриц n-го порядка относительно сложения, умножения;
и) множество матриц n-го порядка с определителем, равным 1, относительно умножения матриц, сложения;
к) множество решений любой заданной системы линейных однородных уравнений относительно сложения;
л) множество трехмерных (n-мерных) арифметических векторов относительно сложения;
м) множество чисел вида 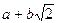 относительно сложения, если a и b – любые рациональные числа;
относительно сложения, если a и b – любые рациональные числа;
н) множество параллельных переносов в плоскости относительно операции их последовательного выполнения;
о) множество многочленов одной и той же степени n от одного аргумента относительно сложения;
п) множество многочленов степени не выше n относительно сложения;
р) множество многочленов от одного аргумента относительно сложения;
с) множество матриц вида 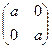 , где
, где  R относительно сложения матриц;
R относительно сложения матриц;
т) множество матриц вида 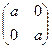 , где
, где  R, а ≠ 0, относительно сложения матриц.
R, а ≠ 0, относительно сложения матриц.
2. Докажите, что множество матриц вида 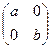 , где a и b –действительные, отличные от нуля числа, составляют группу относительно матричного умножения.
, где a и b –действительные, отличные от нуля числа, составляют группу относительно матричного умножения.
3. Докажите, что множество матриц вида 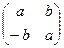 , где a и b – любые, не равные одновременно нулю действительные числа, образует группу относительно матричного умножения.
, где a и b – любые, не равные одновременно нулю действительные числа, образует группу относительно матричного умножения.
4. Докажите, что множество матриц вида 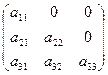 , где a ii ≠ 0 (I = 1, 2, 3), является группой относительно матричного умножения.
, где a ii ≠ 0 (I = 1, 2, 3), является группой относительно матричного умножения.
5. Составьте таблицу умножения элементов симметрической группы S3 подстановок 3-й степени, обозначив элементы этой группы буквами. По таблице найдите взаимно обратные элементы этой группы и докажите, что рассматриваемая группа не является коммутативной.
6. Для множества G 1 = 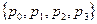 , состоящего из подстановок
, состоящего из подстановок 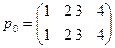 ,
, 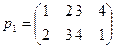 ,
, 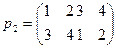 ,
, 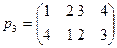 , составьте таблицу умножения и с ее помощью убедитесь, что G 1 – абелева группа.
, составьте таблицу умножения и с ее помощью убедитесь, что G 1 – абелева группа.
7. Дано множество М = 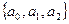 поворотов (вращений) правильного треугольника в плоскости этого треугольника вокруг его центра против часовой стрелки соответственно на углы 0º, 120º, 240º. Эти повороты совмещают треугольник с самим собой. Последовательное выполнение двух любых таких поворотов называется произведением (композицией) этих двух поворотов. Докажите, что М является группой относительно введенной в М операции.
поворотов (вращений) правильного треугольника в плоскости этого треугольника вокруг его центра против часовой стрелки соответственно на углы 0º, 120º, 240º. Эти повороты совмещают треугольник с самим собой. Последовательное выполнение двух любых таких поворотов называется произведением (композицией) этих двух поворотов. Докажите, что М является группой относительно введенной в М операции.
8. На множестве Q \ {0} определено действие 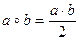 . Докажите, что относительно указанного действия данное множество является группой.
. Докажите, что относительно указанного действия данное множество является группой.
9.Пусть G – множество всевозможных троек чисел вида  и
и 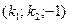 и пусть на G определено действие, выполняемое по правилу
и пусть на G определено действие, выполняемое по правилу 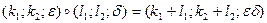 . Докажите, что относительно указанного действия G является группой.
. Докажите, что относительно указанного действия G является группой.
Тема 3. Подгруппы.
Вопросы теории
- Определение подгруппы.
- Циклическая подгруппа. Циклическая группа.
- Образующий циклической группы.
- Порядок элемента группы.
- Порядок группы.
Образцы решения задач
Задача 1. Доказать, что множество А целых чисел, кратных трем, есть подгруппа аддитивной группы Z.
Решение. Имеем:
1) А = 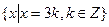 , А Ì Z. (1)
, А Ì Z. (1)
2) Пусть х 1, х 2 – любые элементы из А, то есть х 1 = 3k 1, х 2 = 3k 2, 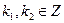 . Так как Z есть аддитивная группа, то
. Так как Z есть аддитивная группа, то 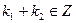 и потому
и потому
 . (2)
. (2)
3) Пусть х = 3k есть любой элемент из А, следовательно, 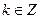 ; тогда и
; тогда и 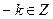 , а потому
, а потому
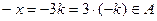 . (3)
. (3)
Из (1), (2), (3) следует, что А есть подгруппа аддитивной группы Z.
Задачи для решения.
1. Докажите, что множество четных чисел является подгруппой аддитивной группы Z целых чисел. Является ли множество нечетных чисел подгруппой группы Z?
2. Пусть п – заданное натуральное число. Показать, что множество целых чисел, кратных п, является подгруппой аддитивной группы Z.
3. Докажите, что множество целых степеней 3 является подгруппой мультипликативной группы Q \ {0}. Запишите эту подгруппу символически. Является ли она циклической? Каков порядок элемента, порождающего эту подгруппу?
4. Найдите порядки элементов  ,
, 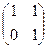 ,
, 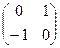 мультипликативной группы невырожденных матриц второго порядка.
мультипликативной группы невырожденных матриц второго порядка.
5. Найдите порядок каждого элемента симметрической группы S3 третьей степени, а затем выясните, какие циклические подгруппы S3 они порождают. Сколько всего различных подгрупп имеет группа S3? Является ли А3 циклической подгруппой группы S3? Каковы ее образующие? (А3 – знакопеременная группа третьей степени.)
6. Найдите порядок элемента а = (1243) 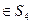 и постройте циклическую подгруппу группы
и постройте циклическую подгруппу группы 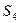 , порожденную элементом а.
, порожденную элементом а.
7. Сколько подгрупп имеет группа 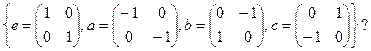
8. Элементы группы G всех самосовмещений квадрата представьте подстановками четвертой степени. Составьте для группы G таблицу Кэли. Изоморфно отобразите группу G на одну из подгрупп симметрической группы S8 восьмой степени.
9. Докажите, что симметрическая группа 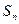 при любом натуральном п ≥ 5 содержит подгруппу, изоморфную знакопеременной группе
при любом натуральном п ≥ 5 содержит подгруппу, изоморфную знакопеременной группе 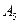 .
.
Дата: 2018-11-18, просмотров: 2675.