Определение 3.23. Функция 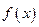 называется непрерывной в точке
называется непрерывной в точке 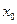 , если: 1) эта функция определена в некоторой окрестности точки
, если: 1) эта функция определена в некоторой окрестности точки 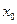 ; 2) существует предел
; 2) существует предел 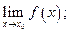 3) этот предел равен значению функции в точке
3) этот предел равен значению функции в точке 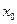 , т.е.
, т.е. 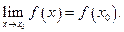
Определение непрерывности функции в точке 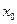 может быть записано и так:
может быть записано и так:
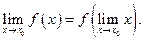
Очевидно, что непрерывность функции в данной точке выражается непрерывностью ее графика при прохождении данной точки. График строится без отрыва карандаша от листа бумаги.
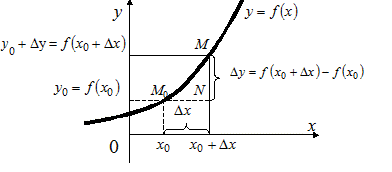 Сформулируем второе определение непрерывности.
Сформулируем второе определение непрерывности.
Дадим аргументу 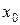 приращение
приращение 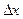 . Тогда функция
. Тогда функция 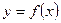 получит приращение
получит приращение 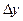 . Приращением аргумента называется разность между наращенным и исходным значением аргумента:
. Приращением аргумента называется разность между наращенным и исходным значением аргумента: 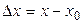 .
.
Рис. 3.23
Приращением функции называется разность между наращенным и исходным значением функции:  (Рис. 3.23).
(Рис. 3.23).
Определение 3.24. Функция 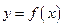 непрерывна в точке
непрерывна в точке 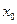 если она определена в некоторой окрестности этой точки и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
если она определена в некоторой окрестности этой точки и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
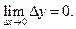
Легко убедится в равносильности этих утверждений. Так, из второго определения следует
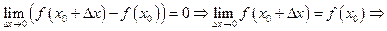
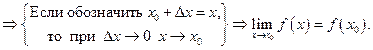
Определение 3.25. Если функция непрерывна в каждой точке некоторого промежутка (интервала, отрезка и т. п.), то она называется непрерывной в этом промежутке.
Пример 3.24. Доказать непрерывность функции 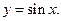
Решение. Найдем приращение функции. 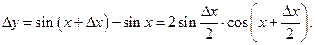
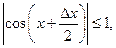 т. е. ограничена.
т. е. ограничена.
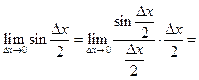
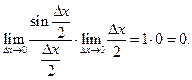
Произведение бесконечно малой на ограниченную есть бесконечно малая величина. Следовательно, 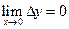 и по второму определению непрерывности функция
и по второму определению непрерывности функция 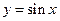 является непрерывной на всей числовой оси.
является непрерывной на всей числовой оси.
Основные теоремы о непрерывных функциях
1. Сумма и произведение конечного числа непрерывных функций есть функция непрерывная.
2. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен нулю.
3. Если функция 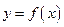 непрерывна в точке
непрерывна в точке 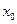 и
и 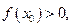 то существует такая окрестность точки
то существует такая окрестность точки 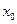 , в которой
, в которой 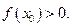
4. Если функция 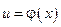 непрерывна в точке
непрерывна в точке 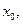 а функция
а функция 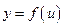 непрерывна в точке
непрерывна в точке 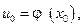 то сложная функция
то сложная функция 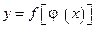 непрерывна в точке
непрерывна в точке 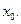
Свойство 4 может быть записано в виде
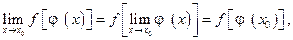
т. е. под знаком непрерывной функции можно переходить к пределу.
5. Элементарные функции непрерывны в области определения.
Теорема. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Условия непрерывности.
Из определения непрерывной функции следует, что функция непрерывна в точке х0, если она определена в этой точке и ее окрестности и
1) право- и левосторонние пределы существуют,
2) эти пределы равны между собой,
3) эти пределы равны значению функции в точке х0. То есть 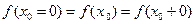 .
.
Дата: 2018-11-18, просмотров: 784.