Определение 3.18. Функция 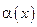 называется бесконечно малой величиной при
называется бесконечно малой величиной при 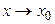 , или при
, или при  если ее предел равен нулю:
если ее предел равен нулю: 
Например, функция 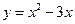 бесконечно малая величина при
бесконечно малая величина при 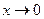 и
и 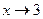 , функция
, функция 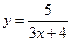 бесконечно малая величина при
бесконечно малая величина при 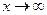 .
.
Определение 3.19. Функции 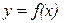 называется бесконечно большой величиной при
называется бесконечно большой величиной при 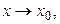 если для любого, сколь угодно большого положительного числа
если для любого, сколь угодно большого положительного числа 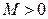 , найдется такое число
, найдется такое число 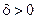 (зависящее от М,
(зависящее от М,  ), что для всех х, не равных
), что для всех х, не равных 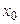 и удовлетворяющих условию
и удовлетворяющих условию  , будет верно
, будет верно 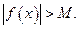
Запись того, что f(х) бесконечно большая при 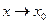 , следующая:
, следующая:  или
или 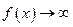 при
при 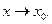
Теорема. Если функция  бесконечно большая при
бесконечно большая при 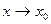
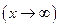 , то функция
, то функция 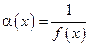 есть величина бесконечно малая при
есть величина бесконечно малая при 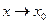
 .
.
Доказательство. Так как f(х) бесконечно большая при 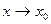 , то для произвольного
, то для произвольного 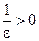 найдется такое число
найдется такое число 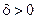 (зависящее от ε,
(зависящее от ε, 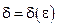 ), что для всех х, не равных
), что для всех х, не равных 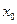 и удовлетворяющих условию
и удовлетворяющих условию 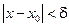 , будет верно
, будет верно  Отсюда следует, что
Отсюда следует, что  ч. т. д. При условии, что
ч. т. д. При условии, что 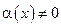 при
при  в некоторой окрестности точки
в некоторой окрестности точки 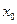 верно и обратное. Если функция α(х) бесконечно малая при
верно и обратное. Если функция α(х) бесконечно малая при 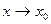
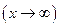 , то функция
, то функция 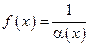 есть величина бесконечно большая при
есть величина бесконечно большая при 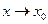
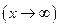 .
.
Свойства бесконечно малых величин
1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную величину (в том числе на постоянную, на другую бесконечно малую) есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
4. Если 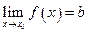 , то
, то 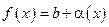 , где
, где 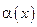 бесконечно малая при
бесконечно малая при 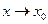 . И наоборот, если
. И наоборот, если 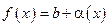 , где
, где 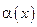 бесконечно малая при
бесконечно малая при 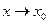 , то
, то 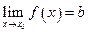 .
.
Далее обозначение 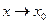 используется для конечных и бесконечных значений предела переменной х. При
используется для конечных и бесконечных значений предела переменной х. При 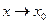 функция
функция  может иметь лишь один предел.
может иметь лишь один предел.
Пример 3.5. Пусть, например, 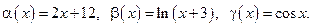 Функции
Функции 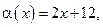
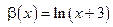 — бесконечно малые при
— бесконечно малые при 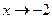 так как
так как 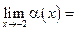
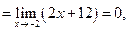
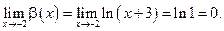 Функция
Функция  ограничена в любом промежутке, а не только в окрестности точки
ограничена в любом промежутке, а не только в окрестности точки 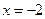 , ибо всегда
, ибо всегда 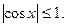 Поэтому функция
Поэтому функция  по свойству 2) и 1) есть величина бесконечно малая при
по свойству 2) и 1) есть величина бесконечно малая при 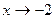 .
.
Основные теоремы о пределах
1. При 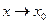 функция
функция  может иметь только один предел.
может иметь только один предел.
2. 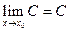
Практическое вычисление пределов основывается на следующих теоремах.
Если существуют  и
и 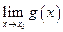 , то
, то
3. 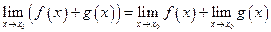 ,
,
4.  ,
, 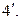
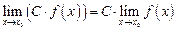 ,
,
5. 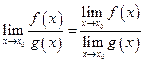 при
при 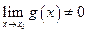 ,
,
6. 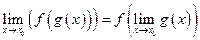 для непрерывных функций (определение непрерывной функции дается ниже).
для непрерывных функций (определение непрерывной функции дается ниже).
7. Если в некоторой окрестности точки х0 (или при достаточно больших х по модулю) 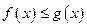 , то
, то 
Признаки существования пределов
Теорема 1. Если в некоторой окрестности точки х0 (или при достаточно больших х по модулю) 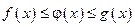 и
и 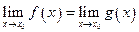 , то
, то 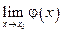 существует и
существует и 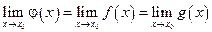 .
.
Теорема 2. Если числовая последовательность 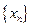 монотонна и ограничена, то она имеет предел.
монотонна и ограничена, то она имеет предел.
Теорема 3. Если в некоторой окрестности точки х0 (или при достаточно больших х по модулю) 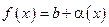 где
где 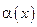 бесконечно малая при
бесконечно малая при 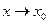 , то существует предел
, то существует предел 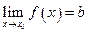 .
.
Односторонние пределы
Определение 3.20. Если 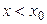 и
и 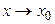 , то употребляют запись
, то употребляют запись 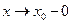 ; если
; если 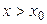 и
и 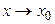 — запись
— запись 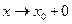 .Числа
.Числа 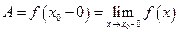 и
и  называются соответственно левым и правым пределом функции f(х) в точке х0.
называются соответственно левым и правым пределом функции f(х) в точке х0.
Теорема. Для существования предела функции f(х) при 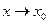 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 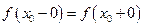 .
.
Пример 3 .6. Например, для функции 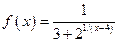
 ,
,
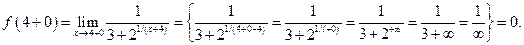
Следовательно, предел 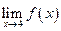 не существует, так как
не существует, так как  (Рис. 3.20).
(Рис. 3.20).
Пример 3.7. Для функции 
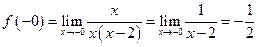 ,
, 
Следовательно, предел 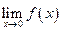 существует:
существует: 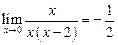 (Рис. 3.21).
(Рис. 3.21).
Графически это выглядит так:
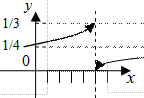

Рис. 3.20 Рис. 3.21
Пример 3.8. Найти 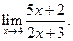
Решение. Так как 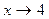 , то числитель дроби стремится к числу
, то числитель дроби стремится к числу  , знаменатель — к числу
, знаменатель — к числу 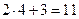 . Следовательно,
. Следовательно, 
Раскрытие неопределенностей
Если при подстановке предельного значения аргумента, не получается определенное число или бесконечность, то в этом случае говорят получена неопределенность. Тогда выражение, стоящее под знаком предела надо преобразовать так, чтобы при подстановке предельного значения получить определенный ответ. Это действие называется раскрытием неопределенности.
Пример 3.9. Найти 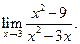
Решение. Здесь числитель и знаменатель дроби при x®3 стремятся к нулю (принято говорить, что имеется неопределенность вида 0/0). Имеем
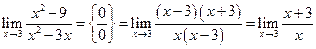 . Если
. Если 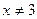 , то
, то 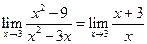 . Но при x®3 дробь (x+3)/3 стремится к числу
. Но при x®3 дробь (x+3)/3 стремится к числу 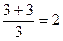 . Итак,
. Итак, 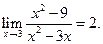
В основном разработаны методы раскрытия неопределенностей вида 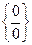 и
и 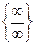 , кроме того, к неопределенностям относятся
, кроме того, к неопределенностям относятся 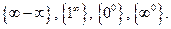
Отметим, что нет неопределенностей в таких ситуациях 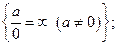
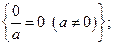
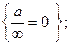
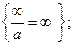
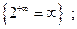
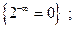
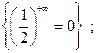
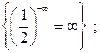
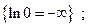
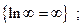
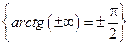 и. т. д.
и. т. д.
Для раскрытия неопределенностей можно применять тождественные преобразования:
1) Если имеется неопределенность вида 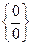 , то в простейших случаях надо числитель и знаменатель разложить на множители и общие множители сократить.
, то в простейших случаях надо числитель и знаменатель разложить на множители и общие множители сократить.
Пример 3.10. Найти 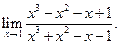
Решение. Здесь имеет место неопределенность вида 0/0. Разложим на множители числитель и знаменатель дроби:
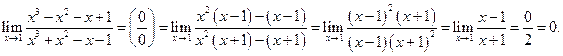
2) Если имеется неопределенность за счет разности квадратных корней, то числитель и знаменатель умножают на сопряженное выражение.
Пример 3.11. Найти 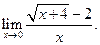
Решение. Умножим числитель и знаменатель дроби на сумму 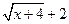 .
.
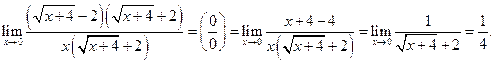
3) Если имеется неопределенность вида 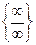 , то в простейших случаях надо числитель и знаменатель разделить на старшие степени (старшие члены) или взять отношения коэффициентов при старших степенях.
, то в простейших случаях надо числитель и знаменатель разделить на старшие степени (старшие члены) или взять отношения коэффициентов при старших степенях.
Пример 3.12. Найти 
Решение. Числитель и знаменатель дроби неограниченно возрастают при x®¥. В таком случае говорят, что имеет место неопределенность вида ¥/¥. Разделив на х числитель и знаменатель дроби, получим  , так как при x®¥ каждая из дробей 5/х и 7/х стремится к нулю.
, так как при x®¥ каждая из дробей 5/х и 7/х стремится к нулю.
Пример 3.13. Найти 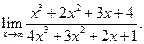
Решение. Это — неопределенность вида ¥/¥. Разделим числитель и знаменатель дроби на старшую степень х, т. е. на х3: 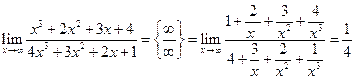 .
.
Пример 3.14. Найти 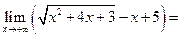

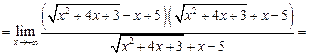
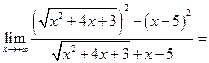
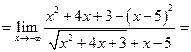
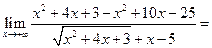
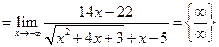
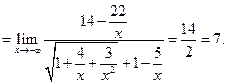
Сравнение бесконечно малых
Пусть 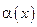 и
и 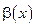 бесконечно малые при
бесконечно малые при 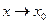 .
.
1. Если 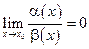 , то говорят, что
, то говорят, что 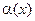 является бесконечно малой высшего порядка малости по сравнению с
является бесконечно малой высшего порядка малости по сравнению с 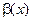 . В этом случае пишут
. В этом случае пишут 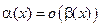 .
.
2. Если 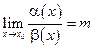 , где m — число, отличное от нуля, то говорят, что
, где m — число, отличное от нуля, то говорят, что 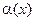 и
и 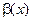 бесконечно малые одного и того же порядка малости. В частности, если
бесконечно малые одного и того же порядка малости. В частности, если 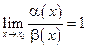 , то бесконечно малые
, то бесконечно малые 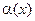 и
и 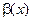 называются эквивалентными. Запись
называются эквивалентными. Запись 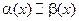 означает, что
означает, что 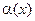 и
и 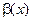 — эквивалентные бесконечно малые.
— эквивалентные бесконечно малые.
3. Если 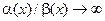 , то это означает, что
, то это означает, что 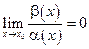 . Таким образом,
. Таким образом, 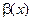 является бесконечно малой высшего порядка малости по сравнению с
является бесконечно малой высшего порядка малости по сравнению с 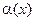 т. е.
т. е. 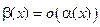 .
.
4. Если  и
и 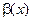 — бесконечно малые одного и того же порядка, причем
— бесконечно малые одного и того же порядка, причем  , то говорят, что бесконечно малая
, то говорят, что бесконечно малая 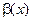 имеет порядок k по сравнению с
имеет порядок k по сравнению с 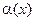 .
.
Отметим некоторые свойства бесконечно малых величин:
1) произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если  , то
, то 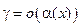 и
и 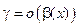 ;
;
2) бесконечно малые 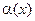 и
и 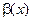 эквивалентны тогда и только тогда, когда их разность
эквивалентны тогда и только тогда, когда их разность 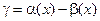 является бесконечно малой высшего порядка по сравнению с
является бесконечно малой высшего порядка по сравнению с 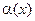 и
и 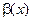 , т. е. если
, т. е. если 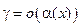 ,
, 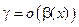 ;
;
3) если 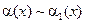 ,
, 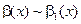 при
при 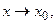 то
то  , т.е. если отношение двух бесконечно малых имеет предел, то этот предел не изменится, если каждую из бесконечно малых заменить эквивалентной бесконечно малой.
, т.е. если отношение двух бесконечно малых имеет предел, то этот предел не изменится, если каждую из бесконечно малых заменить эквивалентной бесконечно малой.
Таким образом, при нахождении пределов бесконечно малые величины можно всегда заменять эквивалентными бесконечно малыми величинами, если они входят в выражение множителями. Если они входят не в виде множителей, то такая замена может не иметь места. В этом случае надо проводить дополнительные исследования.
Замечание. По теореме раздела 3.2.3 свойство 3 может использоваться для бесконечно больших величин. Например, при 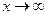
 .
.
Следовательно, при раскрытии неопределенностей можно использовать эквивалентные преобразования. С помощью эквивалентных преобразований пример 3.12 решается следующим образом: 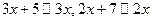 ,
,
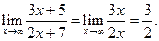
Для примера 3.13 имеем:
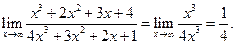
Очевидно, что в этом случае применение эквивалентных преобразований значительно сокращает вычисления и, следовательно, более рационально.
Пример 3.15.
Пусть t — бесконечно малая величина. Сравнить бесконечно малые величины
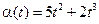 и.
и.  .
.
Решение. Найдем 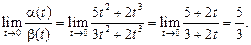
Предел отношения — число, отличное от нуля. Следовательно,  и
и 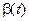 — бесконечно малые одного и того же порядка.
— бесконечно малые одного и того же порядка.
Первый замечательный предел
Определение 3.21. Первым замечательным пределом называется 
 Доказательство.
Доказательство.
Рассмотрим круг радиуса 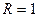 с центром в точке О. Пусть ОВ — подвижный радиус, образующий угол х
с центром в точке О. Пусть ОВ — подвижный радиус, образующий угол х  с осью Ох. Сделаем дополнительные построения, изображенные на чертеже. Из геометрических соображений следуют неравенства:
с осью Ох. Сделаем дополнительные построения, изображенные на чертеже. Из геометрических соображений следуют неравенства:
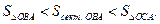
Рис. 3.22
Находим площади, соответствующих фигур и делам очевидные преобразования неравенств:
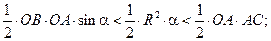
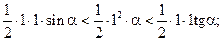
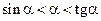
Делим на 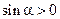 :
:
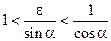 , или
, или
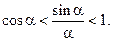
Вычтем у каждой части неравенства единицу:
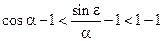 , или
, или
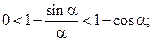

Из 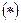 получим, что
получим, что 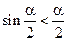 , поэтому
, поэтому
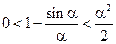 ,
,
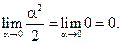
Следовательно, по теореме 1 раздела 3.2.6 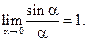
Полученный предел справедлив и для отрицательных α. Действительно, если 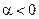 , то сделав замену
, то сделав замену 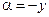
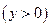 , будем иметь
, будем иметь

Можно показать, что первый замечательный предел имеет место при произвольном стремлении α к нулю.
Замечание. Замена переменных — третий способ, используемый для раскрытия неопределенностей.
Пример 3.16. Найти 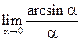 .
.
Решение. 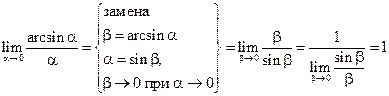 .
.
Пример 3.17. Найти 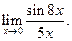
Решение. 
Замечание. 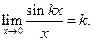 Надо отметить, что
Надо отметить, что 
Пример 3.18. Найти 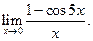
Решение. Имеем 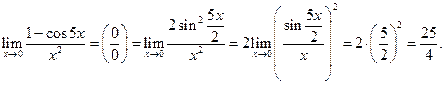
Пример 3.19. Найти 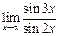 .
.
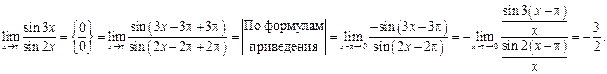
Второй замечательный предел
Рассмотрим числовую последовательность 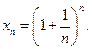 Несмотря на ее необычный вид, она играет огромную роль в математике, экономике, финансовых и экономических исследованиях. Об этом будет сказано ниже.
Несмотря на ее необычный вид, она играет огромную роль в математике, экономике, финансовых и экономических исследованиях. Об этом будет сказано ниже.
Докажем, что эта последовательность имеет предел. Для этого покажем, что она:
1) монотонно возрастающая, 2) ограничена.
Применяя формулу бинома Ньютона, получаем
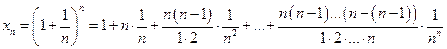 ,
,
или
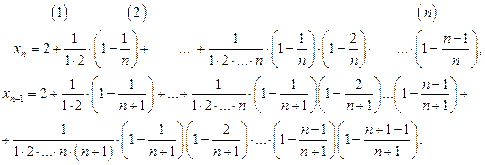
Второе, третье и т. д. n-ое, слагаемые в 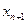 больше соответствующих слагаемых в
больше соответствующих слагаемых в 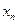 . Кроме того в
. Кроме того в 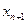 имеется еще оно положительное слагаемое. Поэтому
имеется еще оно положительное слагаемое. Поэтому 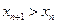 , то есть последовательность
, то есть последовательность 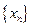 возрастающая.
возрастающая.
Покажем, что последовательность 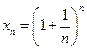 ограничена.
ограничена.
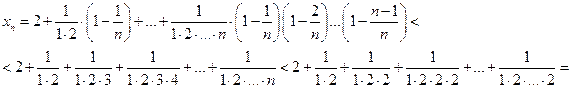
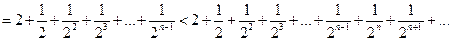
Применяя формулу суммы членов бесконечно убывающей геометрической прогрессии 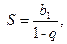 получаем
получаем 
Согласно теореме 2 существования предела, монотонная и ограниченная последовательность 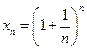 имеет предел.
имеет предел.
Определение 3.22. Числом е называется предел числовой последовательности
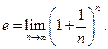
Выше мы установили, что 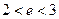 . Можно доказать, что число е — иррациональное число. Вычислено, что
. Можно доказать, что число е — иррациональное число. Вычислено, что 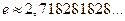
Можно показать, что 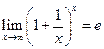 при произвольном стремлении х в бесконечность, а не только тогда, когда х пробегает натуральные значения. (Можно считать, что
при произвольном стремлении х в бесконечность, а не только тогда, когда х пробегает натуральные значения. (Можно считать, что  ).
).
Полагая, 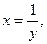 т. е.
т. е.  получаем, что
получаем, что  при
при 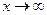 и еще одну запись числа е:
и еще одну запись числа е: 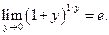
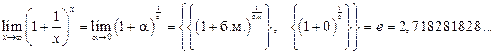
Число е называется неперовым числом, а логарифмы при основании е называются натуральными и обозначаются lnx.
Пример 3.20. Найти 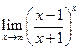 .
.
Решение. Имеем: 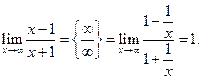
Выполнив соответствующие преобразования, получаем:

В данном случае, не прибегая к общему приему можно найти предел проще:
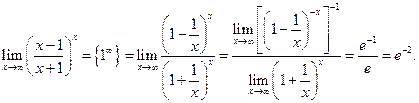
Замечание. При решении примеров полезно иметь в виду следующие равенства:
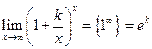 ,
,  ,
, 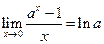 .
.
Таким образом, используя замечательные пределы можно составить
таблицу эквивалентных величин.
При α®0
| sinα~α | arcsinα~α |
| tgα~α | arctgα~α |
| cosα~1-α2/2 | 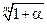 ~1+α/m ~1+α/m
|
| ctgα~1/α | ln(1+α)~α |
| aα~1+αlna | eα~1+α |
Применение этих эквивалентных в большинстве случаев упрощает раскрытие неопределенностей
Пример 3.21. Найти 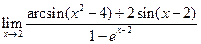 .
.
Решение. 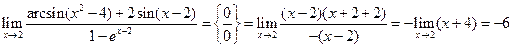 .
.
Пример 3.22. Найти 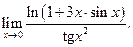
Решение. Заменим числитель и знаменатель дроби эквивалентными бесконечно малыми: 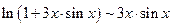 ,
, 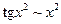 .
.
Тогда 
Пример 3 .23. Найти 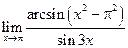 .
.
Решение. 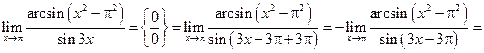
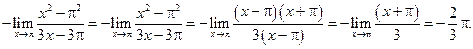
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Дата: 2018-11-18, просмотров: 886.