Четность и нечетность.
Определение 3.8. Функция 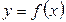 называется четной, если для любых значений х из области определения
называется четной, если для любых значений х из области определения 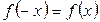 и нечетной, если
и нечетной, если 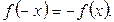 В противном случае функция
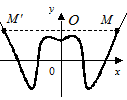
В противном случае функция 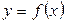 называется функцией общего вида. График четной функции симметричен относительно оси Oy (Рис. 3.6), а график нечетной ― относительно начала координат (Рис. 3.7).
называется функцией общего вида. График четной функции симметричен относительно оси Oy (Рис. 3.6), а график нечетной ― относительно начала координат (Рис. 3.7).
Пример 3.3. Проверить четность функции 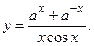
Решение. 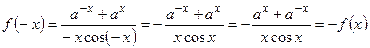 . Функция нечетная.
. Функция нечетная.
Монотонность.
Определение 3.9. Функция 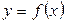 называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 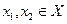 и
и 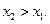 Тогда функция
Тогда функция 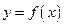 возрастает на промежутке Х, если
возрастает на промежутке Х, если 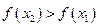 (Рис. 3.8), и убывает, если
(Рис. 3.8), и убывает, если 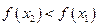 (Рис. 3.9). Такие функции называют строго монотонными.
(Рис. 3.9). Такие функции называют строго монотонными.
Функция 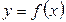 неубывающая на промежутке Х, если
неубывающая на промежутке Х, если 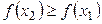 (Рис. 3.13), и невозрастающая, если
(Рис. 3.13), и невозрастающая, если 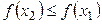 . Такие функции называют монотонными.
. Такие функции называют монотонными.
Ограниченность.
Определение 3.10. Функция 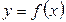 называется ограниченной на промежутке Х, если существует такое положительное число М, что
называется ограниченной на промежутке Х, если существует такое положительное число М, что 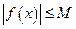 для любого
для любого 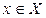 (Рис. 3.10). В противном случае — неограниченной. Если выполняется неравенство
(Рис. 3.10). В противном случае — неограниченной. Если выполняется неравенство 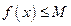
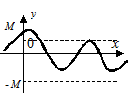
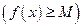 , то функция называется ограниченной сверху (снизу) (Рис. 3.11). Например, функция
, то функция называется ограниченной сверху (снизу) (Рис. 3.11). Например, функция 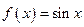 ограничена на всей оси Ох. так как при любом х выполняется неравенство
ограничена на всей оси Ох. так как при любом х выполняется неравенство 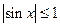 . Примером неограниченной на отрезке
. Примером неограниченной на отрезке 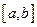 функции может служить функция
функции может служить функция 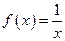 на отрезке
на отрезке 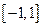 .
.
Периодичность.
Определение 3.11. Функция 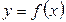 называется периодической с периодом
называется периодической с периодом 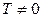 , если для любого х их области определения функции
, если для любого х их области определения функции 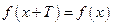 (Рис. 3.12). Основным периодом функции называется положительное наименьшее число T, обладающее указанным свойством.
(Рис. 3.12). Основным периодом функции называется положительное наименьшее число T, обладающее указанным свойством.
| 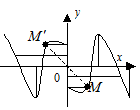
| 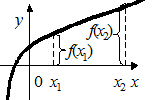
| 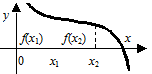
|
| Рис. 3.6 | Рис. 3.7 | Рис. 3.8 | Рис. 3.9 |
| 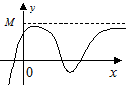
| 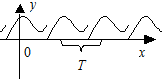
| 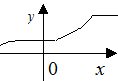
|
| Рис. 3.10 | Рис. 3.11 | Рис. 3.12 | Рис. 3.13 |
Классификация функций
Определение 3.12. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменой. Например, 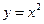 . Функция y аргумента х называется неявной, если она задана уравнением
. Функция y аргумента х называется неявной, если она задана уравнением 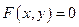 , не разрешенным относительно независимой переменной. Например,
, не разрешенным относительно независимой переменной. Например, 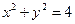 .
.
Определение 3.13. Пусть 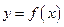 является функцией независимой переменной х, определенной на множестве X с областью значений Y. Поставим в соответствие каждому
является функцией независимой переменной х, определенной на множестве X с областью значений Y. Поставим в соответствие каждому 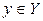 единственное значение
единственное значение 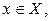 при котором
при котором 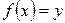 . Тогда полученная функция
. Тогда полученная функция 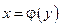 , определенная на множестве с областью значений Х, называется обратной к функции
, определенная на множестве с областью значений Х, называется обратной к функции 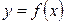 .
.
Так как независимую переменную принято обозначать х, а зависимую — y, то обратную функцию к функции 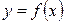 обозначают
обозначают 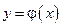 или
или 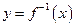 . Чтобы получить явное выражение обратной функции к функции
. Чтобы получить явное выражение обратной функции к функции 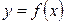 , нужно, если это возможно, разрешить данное уравнение относительно х:
, нужно, если это возможно, разрешить данное уравнение относительно х: 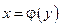 и ввести соответствующие изменения обозначений переменных.
и ввести соответствующие изменения обозначений переменных.
Например, для функции 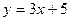 обратной будет функция
обратной будет функция 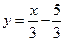 . Для
. Для 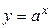 обратная функция
обратная функция 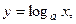 а для
а для 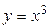 обратная функция
обратная функция 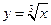 . Не для каждой функции существует однозначная обратная функция. Чтобы значениям y соответствовали единственные значения х, нужно, чтобы прямые, параллельные оси Ох, пересекали график функции не более чем в одной точке.
. Не для каждой функции существует однозначная обратная функция. Чтобы значениям y соответствовали единственные значения х, нужно, чтобы прямые, параллельные оси Ох, пересекали график функции не более чем в одной точке.
Можно доказать, что для любой строго монотонной функции 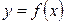 существует обратная функция. Если данная функция не монотонна, то область определения функции разбивают на интервалы, в которых функция монотонна и на каждом интервале находят обратные функции, которые называются ветвями.
существует обратная функция. Если данная функция не монотонна, то область определения функции разбивают на интервалы, в которых функция монотонна и на каждом интервале находят обратные функции, которые называются ветвями.
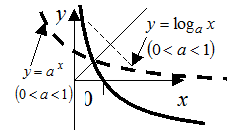 Для
Для 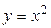 при
при 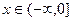 обратной функцией будет
обратной функцией будет 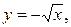 а при
а при 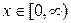 будет
будет 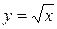
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов 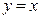 .
.
Рис. 3.14
ТЕОРИЯ ПРЕДЕЛОВ
Дата: 2018-11-18, просмотров: 1022.