Определение 3.14. Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число 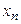, то говорят, что задана числовая последовательность 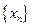, где n=1,2,….

Другими словами, числовая последовательность — это функция натурального аргумента: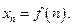

Числа 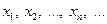 называются членами последовательности, а число  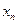— общим или n–м членом данной последовательности.

Примеры числовых последовательностей:

1) 3, 8, 11, 16, …, 3+5n,…(арифметическая прогрессия);

2) 1, -1, 1, -1, …, ,…;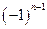

3) 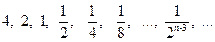 (геометрическая прогрессия).

Если с ростом n члены последовательности 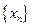 как угодно близко приближаются к некоторому числу a, то число а называется пределом числовой последовательности. Предел числовой последовательности  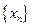обозначается .

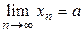Например, легко увидеть, что пределом числовой последовательности 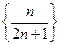 является .

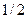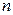
	1	2	5	10	100	1000	10 000	10 000 000	…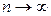
									…

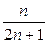
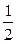
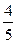
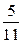
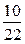
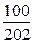
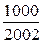
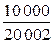
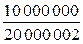
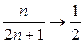
Такими, нестрогими рассуждениями можно найти пределы и других последовательностей, например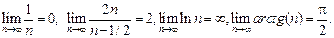

Но при таких рассуждениях, можно ошибиться. Поэтому вводится строгое определение предела числовой последовательности.

Запись 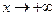означает, что переменная х в процессе изменения становится и остается больше любого наперед заданного числа.

Запись 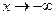означает, что переменная х в процессе изменения становится и остается меньше любого наперед заданного числа.

Запись 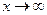означает, что переменная х в процессе изменения становится и остается больше по абсолютной величине любого наперед заданного числа.

Запись 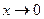означает, что переменная х в процессе изменения становится и остается меньше по абсолютной величине любого наперед заданного положительного числа.

Запись 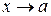означает, что переменная х в процессе изменения становится и остается меньше любого наперед заданного положительного числа (как правило ε>0).

Определение 3.15. Число a называется пределом числовой последовательности 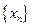, если для любого, сколь угодно малого положительного числа e, найдется такой номер N (зависящий от e, 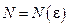), что для всех членов последовательности с номерами  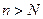выполняется неравенство .

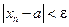Кратко это записывают так

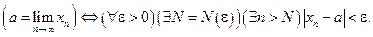
Смысл определения предела числовой последовательности 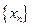 состоит в том, что для достаточно больших n члены последовательности сколь угодно мало отличаются от числа а (по абсолютной величине меньше, чем на число e , каким бы малым оно ни было).

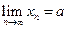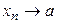В этом случае пишут  или  при 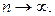 Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.

Пример 3.4. Показать, что при n®¥ последовательность 7/3, 10/5, 13/7, ... , (Зn+4)/(2n+1), ... имеет пределом число 3/2.

Решение. Здесь 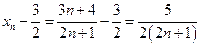. Определим, при каком значении n выполняется неравенство 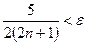; так как 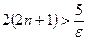. то 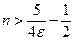. Итак, если  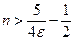то 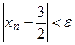, т. е. .

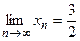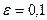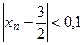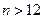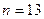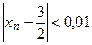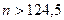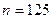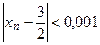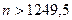Полагая , заключаем, что неравенство  выполняется при  (например, при ). Аналогичным образом, неравенство  выполняется при  (например, при ), а неравенство  при  (например, при ).

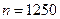Выясним геометрический смысл предела числовой последовательности. Расположим члены последовательности 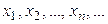 на числовой оси. Неравенство  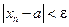равносильно двойному неравенству 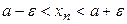, соответствующему попаданию членов последовательности х_n в 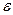-окрестность точки а.

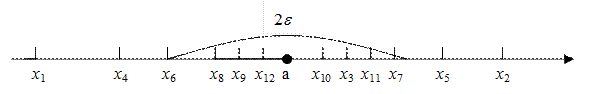Рис. 3.15

Если рассматривать 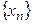 как функцию 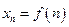, то удобно изображать ее в двухмерной декартовой системе координат:

Рис. 3.16

Для наглядности последовательно члены соединяют отрезками прямых:

Рис. 3.17

Итак, число а есть предел числовой последовательности 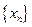, если для любого  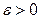найдется номер N, начиная с которого (при 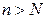) все члены последовательности будут заключены в 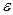– окрестности точки а, какова бы она узкой не была. Вне этой 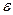– окрестности может быть лишь конечное число членов данной последовательности.

Определение предела функции

Пусть функция 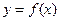задана в некоторой окрестности точки 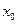, кроме, быть может, самой точки .

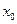Определение 3.16. Число b называется пределом функци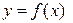и  при 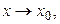 если для любого, сколь угодно малого  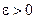найдется такое 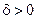(зависящее от ε, 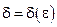), что для всех х, удовлетворяющих условию 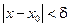, кроме, быть может, самой точки 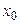, выполняется неравенство  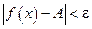(Рис. 3.18).

Кратко это записывают так:

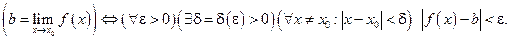
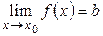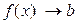Этот предел функции обозначается  или  при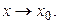

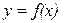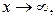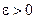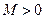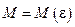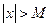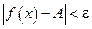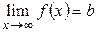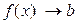Определение 3.17. Число b называется пределом функции  при  если для любого, сколь угодно малого  найдется такое  (зависящее от ε, ), что для всех х таких, что , верно неравенство . Этот предел функции обозначается  или  при 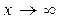 (Рис. 3.19).

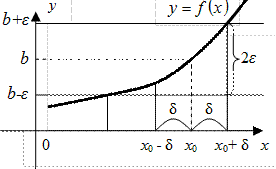
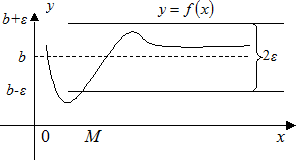
            Рис. 3.18                                       Рис. 3.19

Условно записывают 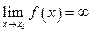, есл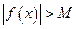и  при 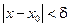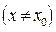, где М— произвольное положительное число.