Стандартные обозначения и названия наиболее распространенных числовых множеств.
 ― множество всех натуральных чисел.
― множество всех натуральных чисел.
 ― множество всех целых чисел.
― множество всех целых чисел.
 ― множество всех неотрицательных целых чисел.
― множество всех неотрицательных целых чисел.
 ― множество всех рациональных целых чисел.
― множество всех рациональных целых чисел.
 ― множество всех рациональных неотрицательных целых чисел.
― множество всех рациональных неотрицательных целых чисел.
Определение 3.3. Иррациональным называют каждое число, которое выражается бесконечной непериодической десятичной дробью. Рациональные и иррациональные числа вместе называются действительными или вещественными числами.
 — множество всех действительных чисел (числовая прямая). Элементы множества R (числа) называются также точками числовой прямой.
— множество всех действительных чисел (числовая прямая). Элементы множества R (числа) называются также точками числовой прямой.
Очевидно, что для множеств  справедливы следующие включения:
справедливы следующие включения:  .
.

 —
—  -окрестность числа
-окрестность числа  (точки
(точки  ).
).
Пример 3.1. Провести операции над множествами А и В:  ,
, 
Решение.  ,
,  ,
,  .
.
Логическая символика
Пусть α и β — некоторые высказывания или утверждения, т. е. предположения, относительно каждого из которых можно сказать, истинно оно или ложно.
Запись  означает: «не α», т.е. отрицание утверждения α.
означает: «не α», т.е. отрицание утверждения α.
Запись  означает: «из утверждения α следует утверждение β». Символ
означает: «из утверждения α следует утверждение β». Символ  — символ импликации.
— символ импликации.
Запись  означает: «утверждение α эквивалентно утверждения β», т.е. из α следует β и из β следует α. Символ
означает: «утверждение α эквивалентно утверждения β», т.е. из α следует β и из β следует α. Символ  — символ эквивалентности.
— символ эквивалентности.
Запись  означает: «α и β». Символ
означает: «α и β». Символ  — символ конъюнкции.
— символ конъюнкции.
Запись  означает: «α или β». Символ
означает: «α или β». Символ  — символ дизъюнкции.
— символ дизъюнкции.
Символ  — символ всеобщности, заменяющий слова «любой», «каждый», «всякий» (all).
— символ всеобщности, заменяющий слова «любой», «каждый», «всякий» (all).
Запись  означает: «для всякого элемента
означает: «для всякого элемента  истинно утверждение α(х)».
истинно утверждение α(х)».
Символ  — символ существования, заменяющий слова «существует», «есть», «найдется» (exist).
— символ существования, заменяющий слова «существует», «есть», «найдется» (exist).
Запись  означает: « существует элемент
означает: « существует элемент  такой, что для него истинно утверждение α(х)».
такой, что для него истинно утверждение α(х)».
3.1.2. Функция одной независимой переменной. Область определения
Определение 3.4. Пусть даны два непустых множества Х и Y. Если каждому элементу х из множества Х по определенному правилу ставится в соответствие один и только один элемент y из Y, то говорят, что на множестве Х задана функция f (или отображение) с множеством значений Y. Это можно записать так: 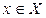 , Х
, Х  Y или f : Х ® Y,
Y или f : Х ® Y,  , где множество Х называется областью определения функции, а множество Y, состоящее из всех чисел вида
, где множество Х называется областью определения функции, а множество Y, состоящее из всех чисел вида  , — множеством значений функции. Область определения функции f обозначается через
, — множеством значений функции. Область определения функции f обозначается через  , а множество значений — через
, а множество значений — через  Значение функции
Значение функции  при
при  обозначают через
обозначают через 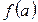 .
.
Область определения функции в простейших случаях представляет собой: интервал (открытый промежуток)  , т.е. совокупность значений х, удовлетворяющих условию
, т.е. совокупность значений х, удовлетворяющих условию  ; сегмент (отрезок, или замкнутый промежуток)
; сегмент (отрезок, или замкнутый промежуток)  , т.е. совокупность значений х, удовлетворяющих условию
, т.е. совокупность значений х, удовлетворяющих условию  ; полуинтервал
; полуинтервал  (т.е.
(т.е.  ) или
) или 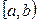 (т.е.
(т.е.  ); бесконечный интервал
); бесконечный интервал  (т.е.
(т.е.  ) или
) или  (т.е.
(т.е.  ) или
) или  (т.е.
(т.е.  ); совокупность нескольких интервалов или сегментов и т. п.
); совокупность нескольких интервалов или сегментов и т. п.
Определение 3.5. Графиком функции  называется множество точек плоскости хOу с координатами
называется множество точек плоскости хOу с координатами  ), где
), где 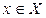 .
.
Определение 3.6. Пусть функция  есть функция от переменой u, определенной на множестве U с областью значений Y, а переменная u в свою очередь, является функцией
есть функция от переменой u, определенной на множестве U с областью значений Y, а переменная u в свою очередь, является функцией  от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция
от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция  называется сложной (или композицией, суперпозицией, функцией от функции).
называется сложной (или композицией, суперпозицией, функцией от функции).
Определение 3.7. Основными элементарными функциями называются функции 




 Элементарными функциями называются функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий +,-,
Элементарными функциями называются функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий +,-,  и конечного числа операций образования сложной функции.
и конечного числа операций образования сложной функции.
Например, 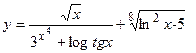 — элементарная функция. А функции
— элементарная функция. А функции 
 ,
,  ,
,  — неэлементарные.
— неэлементарные.
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраическими называются функции, в которых над аргументом проводится конечное число алгебраических действий. Всякая неалгебраическая называется трансцендентной. К числу алгебраических относятся целая рациональная функция (многочлен или полином):  и дробно-рациональная функция — отношение двух многочленов.
и дробно-рациональная функция — отношение двух многочленов.
Функция иррациональная, если в составе операций над аргументом имеется извлечение корня. К трансцендентным относятся показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.
Пример 3.2. Найти область определения функции 
 .
.
Решение. Функция определена, если  и
и  , т. е. если
, т. е. если  и
и  . Область определения функции есть объединение двух интервалов;
. Область определения функции есть объединение двух интервалов;  .
.
3.1.3. Способы задания функции
Существует несколько способов задания функции:
1. Аналитический способ, если функция задана формулой  .
.
2. Табличный способ.
3. Графический способ.
4. Словесный способ.
Примеры аналитического задания функции:  ,
,
 — функция постоянной эластичности. Примером словесного задания функции является функция
— функция постоянной эластичности. Примером словесного задания функции является функция 
Четность и нечетность.
Определение 3.8. Функция 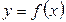 называется четной, если для любых значений х из области определения
называется четной, если для любых значений х из области определения  и нечетной, если
и нечетной, если 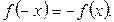 В противном случае функция
В противном случае функция 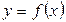 называется функцией общего вида. График четной функции симметричен относительно оси Oy (Рис. 3.6), а график нечетной ― относительно начала координат (Рис. 3.7).
называется функцией общего вида. График четной функции симметричен относительно оси Oy (Рис. 3.6), а график нечетной ― относительно начала координат (Рис. 3.7).
Пример 3.3. Проверить четность функции 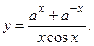
Решение. 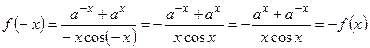 . Функция нечетная.
. Функция нечетная.
Монотонность.
Определение 3.9. Функция 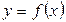 называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть  и
и 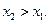 Тогда функция
Тогда функция 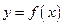 возрастает на промежутке Х, если
возрастает на промежутке Х, если 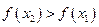 (Рис. 3.8), и убывает, если
(Рис. 3.8), и убывает, если 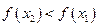 (Рис. 3.9). Такие функции называют строго монотонными.
(Рис. 3.9). Такие функции называют строго монотонными.
Функция 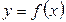 неубывающая на промежутке Х, если
неубывающая на промежутке Х, если  (Рис. 3.13), и невозрастающая, если
(Рис. 3.13), и невозрастающая, если 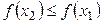 . Такие функции называют монотонными.
. Такие функции называют монотонными.
Ограниченность.
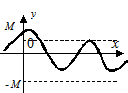
Определение 3.10. Функция 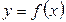 называется ограниченной на промежутке Х, если существует такое положительное число М, что
называется ограниченной на промежутке Х, если существует такое положительное число М, что 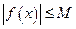 для любого
для любого 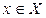 (Рис. 3.10). В противном случае — неограниченной. Если выполняется неравенство
(Рис. 3.10). В противном случае — неограниченной. Если выполняется неравенство 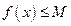
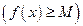 , то функция называется ограниченной сверху (снизу) (Рис. 3.11). Например, функция
, то функция называется ограниченной сверху (снизу) (Рис. 3.11). Например, функция  ограничена на всей оси Ох. так как при любом х выполняется неравенство
ограничена на всей оси Ох. так как при любом х выполняется неравенство 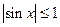 . Примером неограниченной на отрезке
. Примером неограниченной на отрезке  функции может служить функция
функции может служить функция 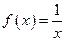 на отрезке
на отрезке  .
.
Периодичность.
Определение 3.11. Функция 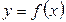 называется периодической с периодом
называется периодической с периодом 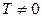 , если для любого х их области определения функции
, если для любого х их области определения функции 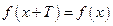 (Рис. 3.12). Основным периодом функции называется положительное наименьшее число T, обладающее указанным свойством.
(Рис. 3.12). Основным периодом функции называется положительное наименьшее число T, обладающее указанным свойством.

| 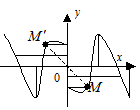
| 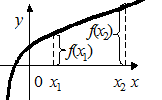
| 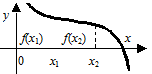
|
| Рис. 3.6 | Рис. 3.7 | Рис. 3.8 | Рис. 3.9 |
| 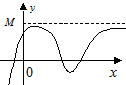
| 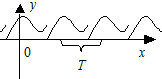
| 
|
| Рис. 3.10 | Рис. 3.11 | Рис. 3.12 | Рис. 3.13 |
Классификация функций
Определение 3.12. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменой. Например, 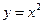 . Функция y аргумента х называется неявной, если она задана уравнением
. Функция y аргумента х называется неявной, если она задана уравнением 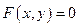 , не разрешенным относительно независимой переменной. Например,
, не разрешенным относительно независимой переменной. Например, 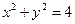 .
.
Определение 3.13. Пусть 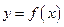 является функцией независимой переменной х, определенной на множестве X с областью значений Y. Поставим в соответствие каждому
является функцией независимой переменной х, определенной на множестве X с областью значений Y. Поставим в соответствие каждому  единственное значение
единственное значение 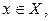 при котором
при котором 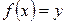 . Тогда полученная функция
. Тогда полученная функция 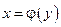 , определенная на множестве с областью значений Х, называется обратной к функции
, определенная на множестве с областью значений Х, называется обратной к функции 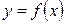 .
.
Так как независимую переменную принято обозначать х, а зависимую — y, то обратную функцию к функции 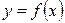 обозначают
обозначают 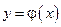 или
или 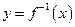 . Чтобы получить явное выражение обратной функции к функции
. Чтобы получить явное выражение обратной функции к функции 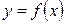 , нужно, если это возможно, разрешить данное уравнение относительно х:
, нужно, если это возможно, разрешить данное уравнение относительно х: 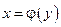 и ввести соответствующие изменения обозначений переменных.
и ввести соответствующие изменения обозначений переменных.
Например, для функции 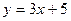 обратной будет функция
обратной будет функция 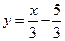 . Для
. Для  обратная функция
обратная функция 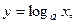 а для
а для 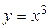 обратная функция
обратная функция 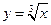 . Не для каждой функции существует однозначная обратная функция. Чтобы значениям y соответствовали единственные значения х, нужно, чтобы прямые, параллельные оси Ох, пересекали график функции не более чем в одной точке.
. Не для каждой функции существует однозначная обратная функция. Чтобы значениям y соответствовали единственные значения х, нужно, чтобы прямые, параллельные оси Ох, пересекали график функции не более чем в одной точке.
Можно доказать, что для любой строго монотонной функции 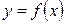 существует обратная функция. Если данная функция не монотонна, то область определения функции разбивают на интервалы, в которых функция монотонна и на каждом интервале находят обратные функции, которые называются ветвями.
существует обратная функция. Если данная функция не монотонна, то область определения функции разбивают на интервалы, в которых функция монотонна и на каждом интервале находят обратные функции, которые называются ветвями.
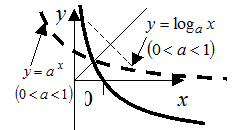 Для
Для 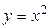 при
при 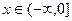 обратной функцией будет
обратной функцией будет  а при
а при 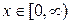 будет
будет 
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов 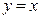 .
.
Рис. 3.14
ТЕОРИЯ ПРЕДЕЛОВ
Кратко это записывают так
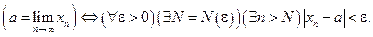
Смысл определения предела числовой последовательности 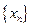 состоит в том, что для достаточно больших n члены последовательности сколь угодно мало отличаются от числа а (по абсолютной величине меньше, чем на число e , каким бы малым оно ни было).
состоит в том, что для достаточно больших n члены последовательности сколь угодно мало отличаются от числа а (по абсолютной величине меньше, чем на число e , каким бы малым оно ни было).
В этом случае пишут 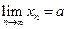 или
или  при
при 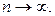 Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.
Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.
Пример 3.4. Показать, что при n®¥ последовательность 7/3, 10/5, 13/7, ... , (Зn+4)/(2n+1), ... имеет пределом число 3/2.
Решение. Здесь 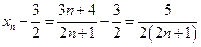 . Определим, при каком значении n выполняется неравенство
. Определим, при каком значении n выполняется неравенство 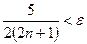 ; так как
; так как 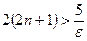 . то
. то 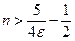 . Итак, если
. Итак, если 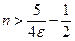 то
то 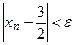 , т. е.
, т. е. 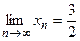 .
.
Полагая 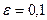 , заключаем, что неравенство
, заключаем, что неравенство 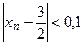 выполняется при
выполняется при  (например, при
(например, при  ). Аналогичным образом, неравенство
). Аналогичным образом, неравенство  выполняется при
выполняется при 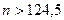 (например, при
(например, при 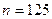 ), а неравенство
), а неравенство  при
при 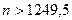 (например, при
(например, при  ).
).
Выясним геометрический смысл предела числовой последовательности. Расположим члены последовательности 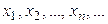 на числовой оси. Неравенство
на числовой оси. Неравенство 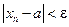 равносильно двойному неравенству
равносильно двойному неравенству  , соответствующему попаданию членов последовательности хn в
, соответствующему попаданию членов последовательности хn в 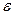 -окрестность точки а.
-окрестность точки а.
 Рис. 3.15
Рис. 3.15
Если рассматривать  как функцию
как функцию 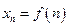 , то удобно изображать ее в двухмерной декартовой системе координат:
, то удобно изображать ее в двухмерной декартовой системе координат:

Рис. 3.16
Для наглядности последовательно члены соединяют отрезками прямых:

Рис. 3.17
Итак, число а есть предел числовой последовательности 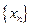 , если для любого
, если для любого 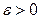 найдется номер N, начиная с которого (при
найдется номер N, начиная с которого (при 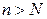 ) все члены последовательности будут заключены в
) все члены последовательности будут заключены в  – окрестности точки а, какова бы она узкой не была. Вне этой
– окрестности точки а, какова бы она узкой не была. Вне этой 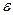 – окрестности может быть лишь конечное число членов данной последовательности.
– окрестности может быть лишь конечное число членов данной последовательности.
Определение предела функции
Пусть функция 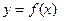 задана в некоторой окрестности точки
задана в некоторой окрестности точки 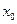 , кроме, быть может, самой точки
, кроме, быть может, самой точки 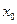 .
.
Определение 3.16. Число b называется пределом функции 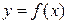 при
при 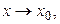 если для любого, сколь угодно малого
если для любого, сколь угодно малого 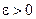 найдется такое
найдется такое 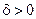 (зависящее от ε,
(зависящее от ε, 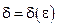 ), что для всех х, удовлетворяющих условию
), что для всех х, удовлетворяющих условию  , кроме, быть может, самой точки
, кроме, быть может, самой точки 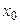 , выполняется неравенство
, выполняется неравенство 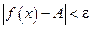 (Рис. 3.18).
(Рис. 3.18).
Кратко это записывают так:
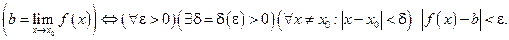
Этот предел функции обозначается 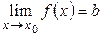 или
или 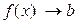 при
при 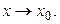
Определение 3.17. Число b называется пределом функции 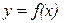 при
при 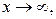 если для любого, сколь угодно малого
если для любого, сколь угодно малого 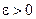 найдется такое
найдется такое 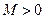 (зависящее от ε,
(зависящее от ε, 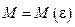 ), что для всех х таких, что
), что для всех х таких, что 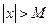 , верно неравенство
, верно неравенство 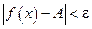 . Этот предел функции обозначается
. Этот предел функции обозначается 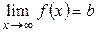 или
или 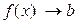 при
при 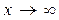 (Рис. 3.19).
(Рис. 3.19).
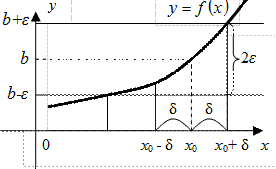
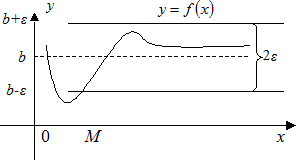
Рис. 3.18 Рис. 3.19
Условно записывают  , если
, если 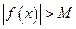 при
при 
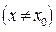 , где М— произвольное положительное число.
, где М— произвольное положительное число.
Основные теоремы о пределах
1. При 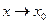 функция
функция  может иметь только один предел.
может иметь только один предел.
2. 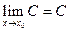
Практическое вычисление пределов основывается на следующих теоремах.
Если существуют  и
и 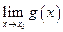 , то
, то
3. 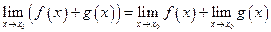 ,
,
4.  ,
, 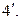
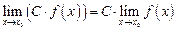 ,
,
5. 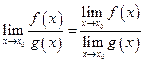 при
при 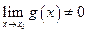 ,
,
6. 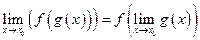 для непрерывных функций (определение непрерывной функции дается ниже).
для непрерывных функций (определение непрерывной функции дается ниже).
7. Если в некоторой окрестности точки х0 (или при достаточно больших х по модулю) 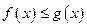 , то
, то 
Односторонние пределы
Определение 3.20. Если 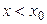 и
и 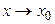 , то употребляют запись
, то употребляют запись 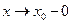 ; если
; если 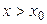 и
и 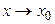 — запись
— запись 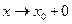 .Числа
.Числа 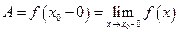 и
и  называются соответственно левым и правым пределом функции f(х) в точке х0.
называются соответственно левым и правым пределом функции f(х) в точке х0.
Теорема. Для существования предела функции f(х) при 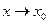 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 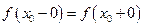 .
.
Пример 3 .6. Например, для функции 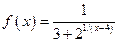
 ,
,
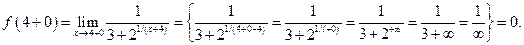
Следовательно, предел 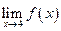 не существует, так как
не существует, так как  (Рис. 3.20).
(Рис. 3.20).
Пример 3.7. Для функции 
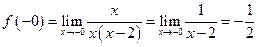 ,
, 
Следовательно, предел 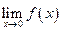 существует:
существует: 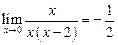 (Рис. 3.21).
(Рис. 3.21).
Графически это выглядит так:
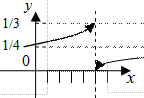

Рис. 3.20 Рис. 3.21
Пример 3.8. Найти 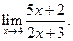
Решение. Так как 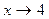 , то числитель дроби стремится к числу
, то числитель дроби стремится к числу  , знаменатель — к числу
, знаменатель — к числу 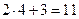 . Следовательно,
. Следовательно, 
Раскрытие неопределенностей
Если при подстановке предельного значения аргумента, не получается определенное число или бесконечность, то в этом случае говорят получена неопределенность. Тогда выражение, стоящее под знаком предела надо преобразовать так, чтобы при подстановке предельного значения получить определенный ответ. Это действие называется раскрытием неопределенности.
Пример 3.9. Найти 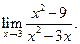
Решение. Здесь числитель и знаменатель дроби при x®3 стремятся к нулю (принято говорить, что имеется неопределенность вида 0/0). Имеем
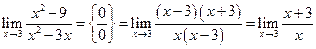 . Если
. Если 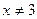 , то
, то 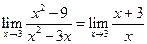 . Но при x®3 дробь (x+3)/3 стремится к числу
. Но при x®3 дробь (x+3)/3 стремится к числу 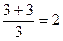 . Итак,
. Итак, 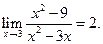
В основном разработаны методы раскрытия неопределенностей вида 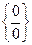 и
и 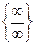 , кроме того, к неопределенностям относятся
, кроме того, к неопределенностям относятся 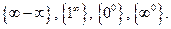
Отметим, что нет неопределенностей в таких ситуациях 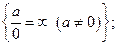
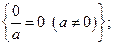
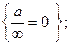
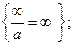
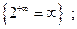
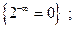
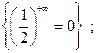
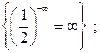
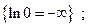
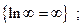
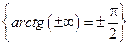 и. т. д.
и. т. д.
Для раскрытия неопределенностей можно применять тождественные преобразования:
1) Если имеется неопределенность вида 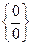 , то в простейших случаях надо числитель и знаменатель разложить на множители и общие множители сократить.
, то в простейших случаях надо числитель и знаменатель разложить на множители и общие множители сократить.
Пример 3.10. Найти 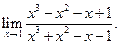
Решение. Здесь имеет место неопределенность вида 0/0. Разложим на множители числитель и знаменатель дроби:
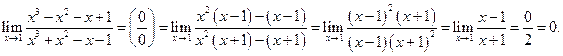
2) Если имеется неопределенность за счет разности квадратных корней, то числитель и знаменатель умножают на сопряженное выражение.
Пример 3.11. Найти 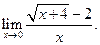
Решение. Умножим числитель и знаменатель дроби на сумму 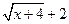 .
.
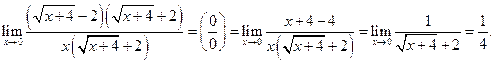
3) Если имеется неопределенность вида 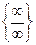 , то в простейших случаях надо числитель и знаменатель разделить на старшие степени (старшие члены) или взять отношения коэффициентов при старших степенях.
, то в простейших случаях надо числитель и знаменатель разделить на старшие степени (старшие члены) или взять отношения коэффициентов при старших степенях.
Пример 3.12. Найти 
Решение. Числитель и знаменатель дроби неограниченно возрастают при x®¥. В таком случае говорят, что имеет место неопределенность вида ¥/¥. Разделив на х числитель и знаменатель дроби, получим  , так как при x®¥ каждая из дробей 5/х и 7/х стремится к нулю.
, так как при x®¥ каждая из дробей 5/х и 7/х стремится к нулю.
Пример 3.13. Найти 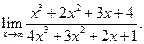
Решение. Это — неопределенность вида ¥/¥. Разделим числитель и знаменатель дроби на старшую степень х, т. е. на х3: 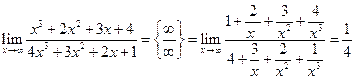 .
.
Пример 3.14. Найти 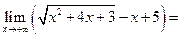

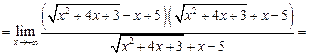
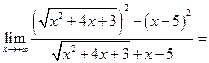
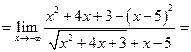
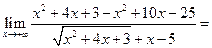
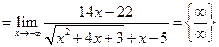
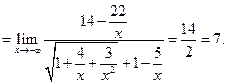
Сравнение бесконечно малых
Пусть 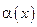 и
и 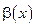 бесконечно малые при
бесконечно малые при 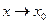 .
.
1. Если 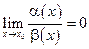 , то говорят, что
, то говорят, что 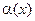 является бесконечно малой высшего порядка малости по сравнению с
является бесконечно малой высшего порядка малости по сравнению с 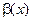 . В этом случае пишут
. В этом случае пишут 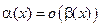 .
.
2. Если 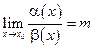 , где m — число, отличное от нуля, то говорят, что
, где m — число, отличное от нуля, то говорят, что 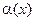 и
и 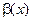 бесконечно малые одного и того же порядка малости. В частности, если
бесконечно малые одного и того же порядка малости. В частности, если 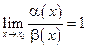 , то бесконечно малые
, то бесконечно малые 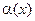 и
и 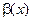 называются эквивалентными. Запись
называются эквивалентными. Запись 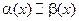 означает, что
означает, что 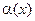 и
и 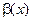 — эквивалентные бесконечно малые.
— эквивалентные бесконечно малые.
3. Если 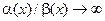 , то это означает, что
, то это означает, что 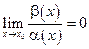 . Таким образом,
. Таким образом, 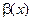 является бесконечно малой высшего порядка малости по сравнению с
является бесконечно малой высшего порядка малости по сравнению с 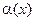 т. е.
т. е. 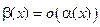 .
.
4. Если  и
и 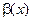 — бесконечно малые одного и того же порядка, причем
— бесконечно малые одного и того же порядка, причем  , то говорят, что бесконечно малая
, то говорят, что бесконечно малая 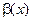 имеет порядок k по сравнению с
имеет порядок k по сравнению с 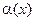 .
.
Отметим некоторые свойства бесконечно малых величин:
1) произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если  , то
, то 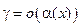 и
и 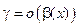 ;
;
2) бесконечно малые 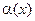 и
и 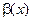 эквивалентны тогда и только тогда, когда их разность
эквивалентны тогда и только тогда, когда их разность 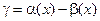 является бесконечно малой высшего порядка по сравнению с
является бесконечно малой высшего порядка по сравнению с 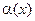 и
и 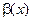 , т. е. если
, т. е. если 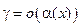 ,
, 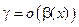 ;
;
3) если 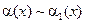 ,
, 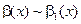 при
при 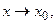 то
то  , т.е. если отношение двух бесконечно малых имеет предел, то этот предел не изменится, если каждую из бесконечно малых заменить эквивалентной бесконечно малой.
, т.е. если отношение двух бесконечно малых имеет предел, то этот предел не изменится, если каждую из бесконечно малых заменить эквивалентной бесконечно малой.
Таким образом, при нахождении пределов бесконечно малые величины можно всегда заменять эквивалентными бесконечно малыми величинами, если они входят в выражение множителями. Если они входят не в виде множителей, то такая замена может не иметь места. В этом случае надо проводить дополнительные исследования.
Замечание. По теореме раздела 3.2.3 свойство 3 может использоваться для бесконечно больших величин. Например, при 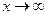
 .
.
Следовательно, при раскрытии неопределенностей можно использовать эквивалентные преобразования. С помощью эквивалентных преобразований пример 3.12 решается следующим образом: 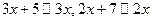 ,
,
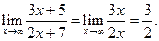
Для примера 3.13 имеем:
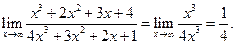
Очевидно, что в этом случае применение эквивалентных преобразований значительно сокращает вычисления и, следовательно, более рационально.
Пример 3.15.
Пусть t — бесконечно малая величина. Сравнить бесконечно малые величины
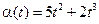 и.
и.  .
.
Решение. Найдем 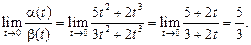
Предел отношения — число, отличное от нуля. Следовательно,  и
и 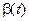 — бесконечно малые одного и того же порядка.
— бесконечно малые одного и того же порядка.
Первый замечательный предел
Определение 3.21. Первым замечательным пределом называется 
 Доказательство.
Доказательство.
Рассмотрим круг радиуса  с центром в точке О. Пусть ОВ — подвижный радиус, образующий угол х
с центром в точке О. Пусть ОВ — подвижный радиус, образующий угол х  с осью Ох. Сделаем дополнительные построения, изображенные на чертеже. Из геометрических соображений следуют неравенства:
с осью Ох. Сделаем дополнительные построения, изображенные на чертеже. Из геометрических соображений следуют неравенства:
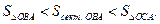
Рис. 3.22
Находим площади, соответствующих фигур и делам очевидные преобразования неравенств:
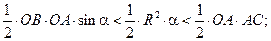
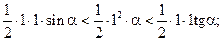
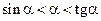
Делим на 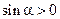 :
:
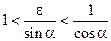 , или
, или
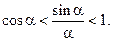
Вычтем у каждой части неравенства единицу:
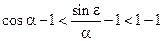 , или
, или
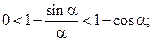

Из 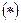 получим, что
получим, что 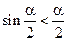 , поэтому
, поэтому
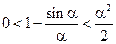 ,
,
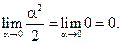
Следовательно, по теореме 1 раздела 3.2.6 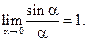
Полученный предел справедлив и для отрицательных α. Действительно, если 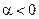 , то сделав замену
, то сделав замену 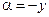
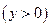 , будем иметь
, будем иметь

Можно показать, что первый замечательный предел имеет место при произвольном стремлении α к нулю.
Замечание. Замена переменных — третий способ, используемый для раскрытия неопределенностей.
Пример 3.16. Найти 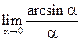 .
.
Решение. 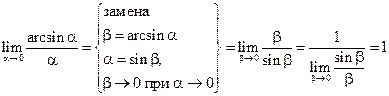 .
.
Пример 3.17. Найти 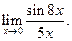
Решение. 
Замечание. 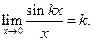 Надо отметить, что
Надо отметить, что 
Пример 3.18. Найти 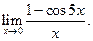
Решение. Имеем 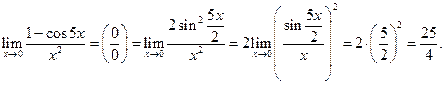
Пример 3.19. Найти 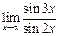 .
.
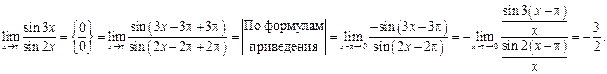
Второй замечательный предел
Рассмотрим числовую последовательность 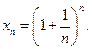 Несмотря на ее необычный вид, она играет огромную роль в математике, экономике, финансовых и экономических исследованиях. Об этом будет сказано ниже.
Несмотря на ее необычный вид, она играет огромную роль в математике, экономике, финансовых и экономических исследованиях. Об этом будет сказано ниже.
Докажем, что эта последовательность имеет предел. Для этого покажем, что она:
1) монотонно возрастающая, 2) ограничена.
Применяя формулу бинома Ньютона, получаем
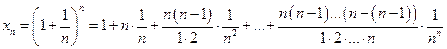 ,
,
или
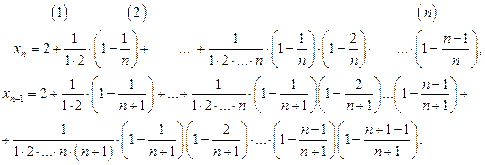
Второе, третье и т. д. n-ое, слагаемые в 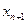 больше соответствующих слагаемых в
больше соответствующих слагаемых в 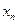 . Кроме того в
. Кроме того в 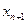 имеется еще оно положительное слагаемое. Поэтому
имеется еще оно положительное слагаемое. Поэтому 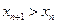 , то есть последовательность
, то есть последовательность 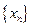 возрастающая.
возрастающая.
Покажем, что последовательность 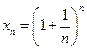 ограничена.
ограничена.
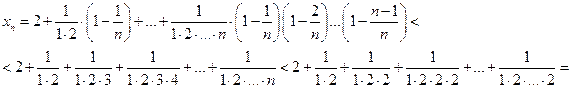
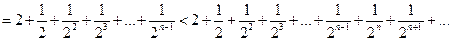
Применяя формулу суммы членов бесконечно убывающей геометрической прогрессии 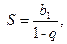 получаем
получаем 
Согласно теореме 2 существования предела, монотонная и ограниченная последовательность 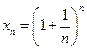 имеет предел.
имеет предел.
Определение 3.22. Числом е называется предел числовой последовательности
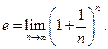
Выше мы установили, что 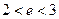 . Можно доказать, что число е — иррациональное число. Вычислено, что
. Можно доказать, что число е — иррациональное число. Вычислено, что 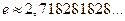
Можно показать, что 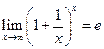 при произвольном стремлении х в бесконечность, а не только тогда, когда х пробегает натуральные значения. (Можно считать, что
при произвольном стремлении х в бесконечность, а не только тогда, когда х пробегает натуральные значения. (Можно считать, что  ).
).
Полагая, 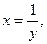 т. е.
т. е.  получаем, что
получаем, что 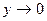 при
при 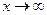 и еще одну запись числа е:
и еще одну запись числа е: 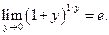
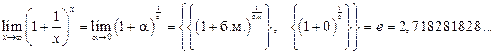
Число е называется неперовым числом, а логарифмы при основании е называются натуральными и обозначаются lnx.
Пример 3.20. Найти 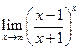 .
.
Решение. Имеем: 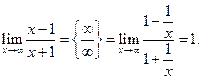
Выполнив соответствующие преобразования, получаем:

В данном случае, не прибегая к общему приему можно найти предел проще:
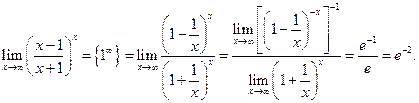
Замечание. При решении примеров полезно иметь в виду следующие равенства:
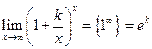 ,
,  ,
, 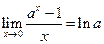 .
.
Таким образом, используя замечательные пределы можно составить
таблицу эквивалентных величин.
При α®0
| sinα~α | arcsinα~α |
| tgα~α | arctgα~α |
| cosα~1-α2/2 | 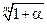 ~1+α/m ~1+α/m
|
| ctgα~1/α | ln(1+α)~α |
| aα~1+αlna | eα~1+α |
Применение этих эквивалентных в большинстве случаев упрощает раскрытие неопределенностей
Пример 3.21. Найти 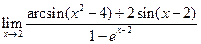 .
.
Решение. 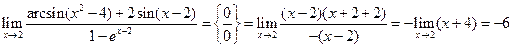 .
.
Пример 3.22. Найти 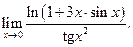
Решение. Заменим числитель и знаменатель дроби эквивалентными бесконечно малыми: 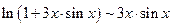 ,
, 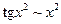 .
.
Тогда 
Пример 3 .23. Найти 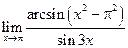 .
.
Решение. 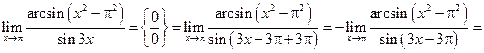
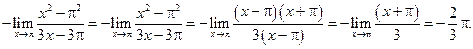
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Условия непрерывности.
Из определения непрерывной функции следует, что функция непрерывна в точке х0, если она определена в этой точке и ее окрестности и
1) право- и левосторонние пределы существуют,
2) эти пределы равны между собой,
3) эти пределы равны значению функции в точке х0. То есть  .
.
Асимптоты
Определение 3.27. Прямая называется асимптотой для кривой, если расстояние от точки кривой до этой прямой стремится к нулю при отдалении точки в бесконечность.



Рис. 3.32 Рис. 3.33 Рис. 3.34
Из рис. 3.34 можно сделать вывод, что график функции может иметь любое число (в том числе бесконечное множество) вертикальных асимптот, но не более двух наклонных или горизонтальных: левую и правую. График функции может пресекать наклонные и горизонтальные асимптоты, но не может пересекать вертикальные асимптоты. Выведем уравнения асимптот.
Рассмотрим вначале вертикальные асимптоты.
Пусть график функции имеет вертикальную асимптоту  . Возьмем точку
. Возьмем точку  на графике функции. В этом случае обязательно
на графике функции. В этом случае обязательно  , так как в противном случае точка Р не удалялась бы неограниченно от начала координат. Верно и обратное утверждение: если
, так как в противном случае точка Р не удалялась бы неограниченно от начала координат. Верно и обратное утверждение: если  , то
, то  — вертикальная асимптота. Таким образом,
— вертикальная асимптота. Таким образом,  — вертикальная асимптота, если
— вертикальная асимптота, если  .
.
Чтобы установить взаимное расположение ветвей линии и асимптоты исследуют знак бесконечности  , к которому стремится
, к которому стремится  , когда х стремится слева и справа к точке
, когда х стремится слева и справа к точке 
Поэтому вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения в конечных точках (открытые концы области определения).
Пусть  — наклонная асимптота. Возьмем точку
— наклонная асимптота. Возьмем точку  на графике функции. Из определения асимптоты
на графике функции. Из определения асимптоты  .
.
Используя формулу расстояния от точки до прямой имеем  Отсюда тем более и
Отсюда тем более и  Предел третьего слагаемого равен нулю, поэтому, получаем
Предел третьего слагаемого равен нулю, поэтому, получаем  Но так как
Но так как  то
то 
Таким образом, если существует наклонная асимптота 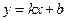 , то ее параметры находятся по формулам
, то ее параметры находятся по формулам  ,
, 
Ясно, что верно и обратное: если эти пределы существуют, график функции имеет асимптоту. Если бы, хотя бы один из пределов не существует, то наклонной асимптоты нет.
Для горизонтальной асимптоты  Поэтому горизонтальная асимптота имеет уравнение
Поэтому горизонтальная асимптота имеет уравнение  где
где 
Если асимптотическое изменение функции различно при стремлении х к положительной или к отрицательной бесконечности, то следует раздельно рассматривать случаи  и
и 
Пример 3.29. Найти вертикальные и горизонтальные асимптоты графика функции  .
.
Решение. D(y)=(-∞,-4)  (-4,4)
(-4,4)  (4,+∞). Следовательно, исследуем точки±4.
(4,+∞). Следовательно, исследуем точки±4.
 . Поэтому линия имеет две вертикальные асимптоты
. Поэтому линия имеет две вертикальные асимптоты 
 Поэтому линия имеет одну горизонтальную асимптоту
Поэтому линия имеет одну горизонтальную асимптоту 
Пример 3.30. Найти асимптоты графика функции  .
.
Решение. D(y)=(-∞,2)  (2,+∞). Линия имеет оду вертикальную асимптоту, горизонтальных асимптот не имеет. Наклонные ищем в виде
(2,+∞). Линия имеет оду вертикальную асимптоту, горизонтальных асимптот не имеет. Наклонные ищем в виде  , где
, где
 ,
,
 Линия имеет наклонную асимптоту
Линия имеет наклонную асимптоту 
Ее можно найти выделением линейной части:

при больших х.
3.3.4. Основные свойства функции, непрерывной на отрезке 
Перечислим, не доказывая, основные свойства функции, непрерывной на отрезке  .
.
Теорема І. Всякая непрерывная на отрезке  функция ограничена на этом отрезке (Рис. 3.35).
функция ограничена на этом отрезке (Рис. 3.35).
Определение 3.28. Наибольшим (наименьшим) значением функции  на отрезке
на отрезке  называется такое значение
называется такое значение  , что для всех точек х отрезка
, что для всех точек х отрезка  выполняется неравенство
выполняется неравенство 
 .
.
Теорема 2. Функция, непрерывная на отрезке  , принимает, по крайней мере, в одной его точке наибольшее значение и по крайней мере в одной его точке — наименьшее значение (Рис. 3.36).
, принимает, по крайней мере, в одной его точке наибольшее значение и по крайней мере в одной его точке — наименьшее значение (Рис. 3.36).
Теорема 3. Функция, непрерывная на отрезке  , принимающая на концах этого отрезка значения противоположных знаков, по крайней мере, в одной точке отрезка
, принимающая на концах этого отрезка значения противоположных знаков, по крайней мере, в одной точке отрезка  обращается в нуль (Рис. 3.37).
обращается в нуль (Рис. 3.37).
Теорема 4. Функция, непрерывная на отрезке  , принимает в этом отрезке все промежуточные значения между своими наибольшим и наименьшим значениями, соответственно М и m.
, принимает в этом отрезке все промежуточные значения между своими наибольшим и наименьшим значениями, соответственно М и m.
Примечание. Из определения функции, ограниченной на отрезке  , следует, что график такой функции целиком располагается между прямыми
, следует, что график такой функции целиком располагается между прямыми  и
и  . Например, график функции
. Например, график функции  , как известно, целиком располагается между прямыми
, как известно, целиком располагается между прямыми  и
и  .
.
 Рис. 3. 35 Рис. 3. 36 Рис. 3. 37
Рис. 3. 35 Рис. 3. 36 Рис. 3. 37
ЛИТЕРАТУРА
Для содержательных модулей
1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.
Стандартные обозначения и названия наиболее распространенных числовых множеств.
 ― множество всех натуральных чисел.
― множество всех натуральных чисел.
 ― множество всех целых чисел.
― множество всех целых чисел.
 ― множество всех неотрицательных целых чисел.
― множество всех неотрицательных целых чисел.
 ― множество всех рациональных целых чисел.
― множество всех рациональных целых чисел.
 ― множество всех рациональных неотрицательных целых чисел.
― множество всех рациональных неотрицательных целых чисел.
Определение 3.3. Иррациональным называют каждое число, которое выражается бесконечной непериодической десятичной дробью. Рациональные и иррациональные числа вместе называются действительными или вещественными числами.
 — множество всех действительных чисел (числовая прямая). Элементы множества R (числа) называются также точками числовой прямой.
— множество всех действительных чисел (числовая прямая). Элементы множества R (числа) называются также точками числовой прямой.
Очевидно, что для множеств  справедливы следующие включения:
справедливы следующие включения:  .
.

 —
—  -окрестность числа
-окрестность числа  (точки
(точки  ).
).
Пример 3.1. Провести операции над множествами А и В:  ,
, 
Решение.  ,
,  ,
,  .
.
Логическая символика
Пусть α и β — некоторые высказывания или утверждения, т. е. предположения, относительно каждого из которых можно сказать, истинно оно или ложно.
Запись  означает: «не α», т.е. отрицание утверждения α.
означает: «не α», т.е. отрицание утверждения α.
Запись  означает: «из утверждения α следует утверждение β». Символ
означает: «из утверждения α следует утверждение β». Символ  — символ импликации.
— символ импликации.
Запись  означает: «утверждение α эквивалентно утверждения β», т.е. из α следует β и из β следует α. Символ
означает: «утверждение α эквивалентно утверждения β», т.е. из α следует β и из β следует α. Символ  — символ эквивалентности.
— символ эквивалентности.
Запись  означает: «α и β». Символ
означает: «α и β». Символ  — символ конъюнкции.
— символ конъюнкции.
Запись  означает: «α или β». Символ
означает: «α или β». Символ  — символ дизъюнкции.
— символ дизъюнкции.
Символ  — символ всеобщности, заменяющий слова «любой», «каждый», «всякий» (all).
— символ всеобщности, заменяющий слова «любой», «каждый», «всякий» (all).
Запись  означает: «для всякого элемента
означает: «для всякого элемента  истинно утверждение α(х)».
истинно утверждение α(х)».
Символ  — символ существования, заменяющий слова «существует», «есть», «найдется» (exist).
— символ существования, заменяющий слова «существует», «есть», «найдется» (exist).
Запись  означает: « существует элемент
означает: « существует элемент  такой, что для него истинно утверждение α(х)».
такой, что для него истинно утверждение α(х)».
3.1.2. Функция одной независимой переменной. Область определения
Определение 3.4. Пусть даны два непустых множества Х и Y. Если каждому элементу х из множества Х по определенному правилу ставится в соответствие один и только один элемент y из Y, то говорят, что на множестве Х задана функция f (или отображение) с множеством значений Y. Это можно записать так: 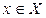 , Х
, Х  Y или f : Х ® Y,
Y или f : Х ® Y,  , где множество Х называется областью определения функции, а множество Y, состоящее из всех чисел вида
, где множество Х называется областью определения функции, а множество Y, состоящее из всех чисел вида  , — множеством значений функции. Область определения функции f обозначается через
, — множеством значений функции. Область определения функции f обозначается через  , а множество значений — через
, а множество значений — через  Значение функции
Значение функции  при
при  обозначают через
обозначают через 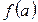 .
.
Область определения функции в простейших случаях представляет собой: интервал (открытый промежуток)  , т.е. совокупность значений х, удовлетворяющих условию
, т.е. совокупность значений х, удовлетворяющих условию  ; сегмент (отрезок, или замкнутый промежуток)
; сегмент (отрезок, или замкнутый промежуток)  , т.е. совокупность значений х, удовлетворяющих условию
, т.е. совокупность значений х, удовлетворяющих условию  ; полуинтервал
; полуинтервал  (т.е.
(т.е.  ) или
) или 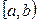 (т.е.
(т.е.  ); бесконечный интервал
); бесконечный интервал  (т.е.
(т.е.  ) или
) или  (т.е.
(т.е.  ) или
) или  (т.е.
(т.е.  ); совокупность нескольких интервалов или сегментов и т. п.
); совокупность нескольких интервалов или сегментов и т. п.
Определение 3.5. Графиком функции  называется множество точек плоскости хOу с координатами
называется множество точек плоскости хOу с координатами  ), где
), где 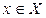 .
.
Определение 3.6. Пусть функция  есть функция от переменой u, определенной на множестве U с областью значений Y, а переменная u в свою очередь, является функцией
есть функция от переменой u, определенной на множестве U с областью значений Y, а переменная u в свою очередь, является функцией  от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция
от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция  называется сложной (или композицией, суперпозицией, функцией от функции).
называется сложной (или композицией, суперпозицией, функцией от функции).
Определение 3.7. Основными элементарными функциями называются функции 




 Элементарными функциями называются функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий +,-,
Элементарными функциями называются функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий +,-,  и конечного числа операций образования сложной функции.
и конечного числа операций образования сложной функции.
Например, 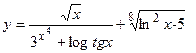 — элементарная функция. А функции
— элементарная функция. А функции 
 ,
,  ,
,  — неэлементарные.
— неэлементарные.
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраическими называются функции, в которых над аргументом проводится конечное число алгебраических действий. Всякая неалгебраическая называется трансцендентной. К числу алгебраических относятся целая рациональная функция (многочлен или полином):  и дробно-рациональная функция — отношение двух многочленов.
и дробно-рациональная функция — отношение двух многочленов.
Функция иррациональная, если в составе операций над аргументом имеется извлечение корня. К трансцендентным относятся показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.
Пример 3.2. Найти область определения функции 
 .
.
Решение. Функция определена, если  и
и  , т. е. если
, т. е. если  и
и  . Область определения функции есть объединение двух интервалов;
. Область определения функции есть объединение двух интервалов;  .
.
3.1.3. Способы задания функции
Существует несколько способов задания функции:
1. Аналитический способ, если функция задана формулой  .
.
2. Табличный способ.
3. Графический способ.
4. Словесный способ.
Примеры аналитического задания функции:  ,
,
 — функция постоянной эластичности. Примером словесного задания функции является функция
— функция постоянной эластичности. Примером словесного задания функции является функция 
Дата: 2018-11-18, просмотров: 870.