Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.

Пусть область D является прямоугольником со сторонами, параллельными осям координат.

                                                 Рис. 7.8

Теорема. Если функция 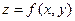 непрерывна в прямоугольной области 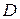, то она интегрируема в  и

.

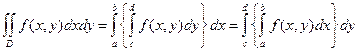Таким образом, вычисление двойного интеграла сводится к повторному интегрированию — вычисляются однократные интегралы, причем, как и в случае дифференциального исчисления, интегрируя по 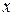, с переменной  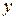действуем как с постоянной величиной и наоборот. Записывается это равенство также в виде:

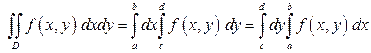               .                 (7.20)

В случае произвольной области 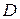, поместим ее в прямоугольник со сторонами, параллельными осям координат (рис. 7.9) так, чтобы эту область можно было записать одним из двух способов с помощью неравенств:

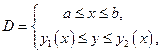
или

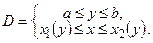
Рис. 7.9

Тогда двойной интеграл по области 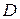 вычисляется по формулам:

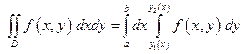                                                           (7.21)

или

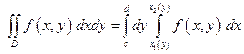                         .                             (7.22)

Нужно только помнить, что во внутреннем интеграле одна из переменных принимается при интегрировании за постоянную. Таким образом, вычисление двойного интеграла сводится к повторному (или двукратному) интегрированию.

Пример 7.25. Найти двойной интеграл 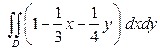 по прямоугольной области .

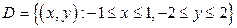Решение.

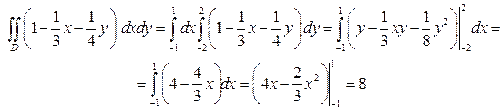
или

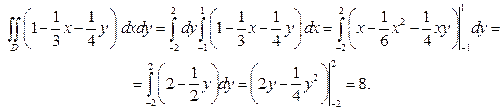
Пример 7.26. Вычислить 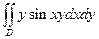, где .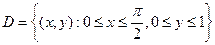

Решение.

.

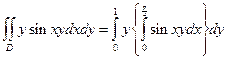Вычислим однократный интеграл

,

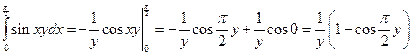затем подставим

.

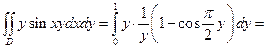
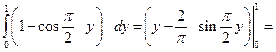
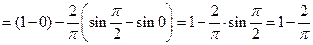Пример 7.27. Найти двойной интеграл 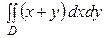 по области D , ограниченной линиям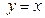и  и .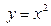

Решение.

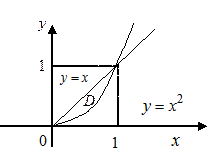
                                                       Рис. 7.10

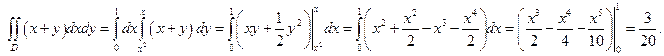
ЛИТЕРАТУРА

Для содержательных модулей

1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.

2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.

Основная

1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.

2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.

3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.

4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.

5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.

6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.

7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.

8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.

Сборники задач

1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.

2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.