Лекция 14
Определённый интеграл. Теорема Ньютона-Лейбница. Методы интегрирования определённого интеграла.
Вопросы:
1. Понятие определённого интеграла.
2. Теорема о среднем значении.
3. Формула Ньютона-Лейбница.
4. Замена переменной в определённом интеграле.
5. Интегрирование по частям в определённом интеграле.
6. Несобственные интегралы первого и второго рода.
7. Вычисление площадей плоских фигур.
8. Вычисление объёмов тел вращения.
9. Экономические приложения определённого интеграла.
10. Понятие двойного интеграла.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Задачи, приводящие к понятию определенного интеграла
Широкое применение в различных областях науки, в том числе в экономике, математическом моделировании, имеет место одно из основных понятий математического анализа — определенный интеграл. Рассмотрим некоторые задачи, приводящие к определенному интегралу.
Задача 1. Пусть на отрезке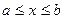 
определена непрерывная функция 
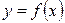. Будем предполагать, что на этом отрезке 
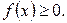Криволинейной трапецией называют фигуру, ограниченную кривой 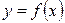, отрезком 
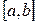оси Ох, прямыми 
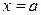и 
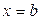(рис. 7.1). Для вычисления площади криволинейной трапеции разделим отрезок 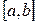(основание трапеции) произвольным образом точками 
на n частей так, что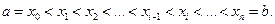 
Пусть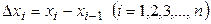 
— длина этих частей. Наибольшую из этих разностей в дальнейшем будем обозначать 
Через каждую точку деления проведем прямую, параллельно оси О y, до пересечения с кривой 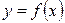. Заменим каждую элементарную трапецию прямоугольником с основанием 
и высотой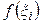 
, где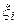 
— произвольная точка отрезка 
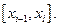Площадь каждого такого прямоугольника равна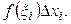 
Рис. 7.1
Сумму площадей всех этих прямоугольников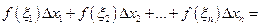 
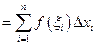можно рассматривать как приближенную величину площади криволинейной трапеции, т. е.
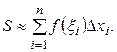
Чтобы найти точное значение площади криволинейной трапеции надо перейти к пределу, при 
Таким образом,
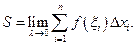(7.1)
Задача 2. Известно, что потребление электроэнергии в течение суток меняется. Предположим, что 
— функция, характеризующая потребление электроэнергии, где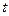 
— время. Требуется определить количество электроэнергии, потребленной за период времени 
.
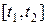Решение. Общее количество потребляемой электроэнергии можно рассматривать как сумму количеств электроэнергии, потребляемой на малых промежутках от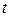 
до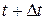 
. Если предположить, что в течение этого промежутка не меняется, то суммарный объем потребленной электроэнергии равен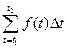 
и
.
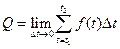На практике это действие осуществляется счетчиками электроэнергии.
Доказательство.
Обозначим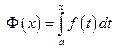 
. Нужно доказать, что 
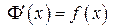. Для этого применим определение производной. Пусть 
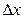— приращение аргумента. Тогда
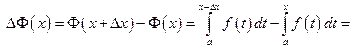
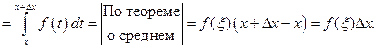
Теперь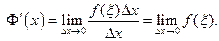 
Функция 
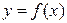непрерывна в точке х, поэтому 
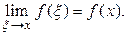Наконец 
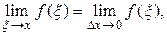так как ξ лежит между х и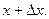 
Из этой теоремы легко получить формулу для вычисления определенного интеграла. По доказанной теореме 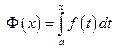— первообразная для функции 
Поэтому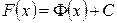 
— произвольная первообразная для Получим:
.
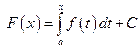Найдем постоянную С.
.
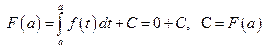Следовательно,
.
Отсюда получаем формулу, называемую формулой Ньютона-Лейбница:
, (7.6)
где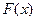 
— некоторая первообразная для 
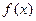, т.е. 
.
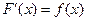Пример 7.1. Вычислить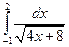 
.
Решение.
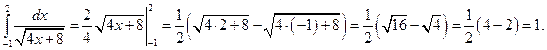
Пример 7.2. Вычислить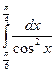 
.
Решение.
.
Теорема.
, (7.7)
где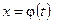 
— функция, непрерывная вместе со своей производной 
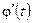на отрезке 
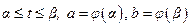, а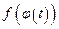 
— функция, непрерывная на [α,β].
Доказательство. Пусть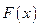 
— первообразная для функции 
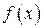на отрезке 
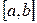. Тогда 
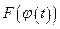— первообразная функции 
на [α,β]. Действительно 
Применяя дважды формулу Ньютона — Лейбница, получаем
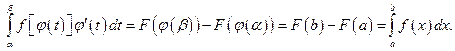
Замечание. Если 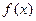— нечетная функция, т. е. 
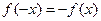, то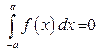 
. Если 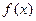— четная функция, т. е. 
, то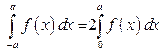 
.
Пример 7.3. Вычислить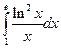 
.
Решение. Положим 
; если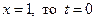 
; если 
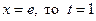. Тогда
Пример 7.4. Вычислить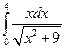 
.
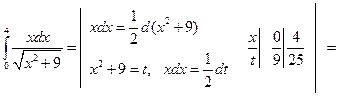
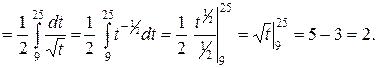
Пример 7.5. Вычислить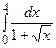 
.
Решение. Положим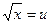 
. Тогда 
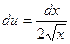, откуда 
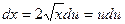. Когда переменная х изменяется от 0 до 4, то переменная 
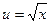изменяется от 0 до 2. Таким образом, после замены переменной у определенного интеграла изменяются пределы интегрирования. Итак, имеем
.
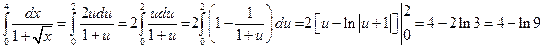Замечание. Отсюда видно, что разница в применении замены переменной в неопределенном и определенном интеграле состоит в том, что во втором случае не приходится возвращаться к старой переменной, так как при замене переменной изменяются также и пределы интегрирования.
Теорема.
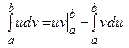, (7.8)
где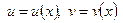 
— непрерывно дифференцируемые функции на отрезке [а,b].
Доказательство. Применим формулу Ньютона — Лейбница к равенству
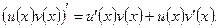Получим
.
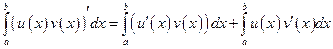Отсюда 
т.к. по определению дифференциала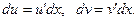 
Пример 7.6. Вычислить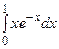 
.
Решение. Воспользуемся методом интегрирования по частям. Положим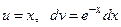 
, откуда 
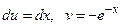. Тогда
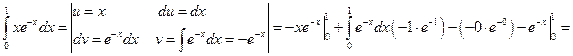
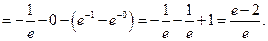
Пример 7.7.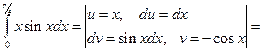 
.
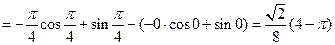Пример 7.8. Вычислить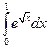 
.
Решение. Сначала воспользуемся методом замены переменных, затем проинтегрируем полученный интеграл по частям.
.
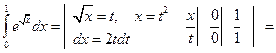
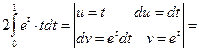
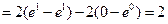НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Решение.
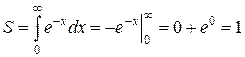(кв. ед.).
Решение.
. 
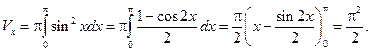
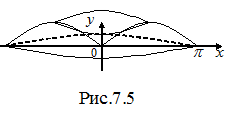
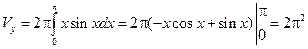Пример 7.17. Найти объем тела вращения относительно оси 
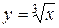фигуры, ограниченной линиями 
и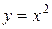 
.
Решение. Необходимо преобразовать функции к виду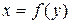 
: 
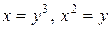. Точки пересечения этих кривых 
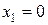и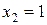 
. Тогда
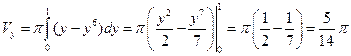(куб. ед.).
Пример 7.18. Найти объем тела вращения фигуры, образованной линией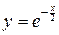 
, относительно ее асимптоты при 
.
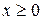Решение. Поскольку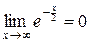 
, то уравнение горизонтальной асимптоты 
и необходимо использовать формулы объема тела вращения относительно оси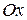 
:
(ед. куб.).
7.4. ЭКОНОМИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
Пример 7.19. В задаче 2 (п. 7.1.1) потребление электроэнергии можно рассматривать как кусочно-непрерывную, ограниченную на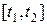 
функцию. Поэтому:
.
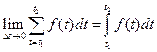Пример 7.20. Предположим, что годовой доход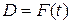 
есть функция времени 
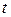. Пусть удельная норма процента равна 
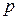и проценты исчисляются непрерывно. Определить дисконтированный объем дохода, полученного за 
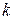лет. (Дисконтирование — определение начальной суммы по известной конечной величине).
Решение. За промежуток времени от 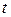до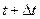 
, при непрерывном начислении процентов, дисконтируемый доход составит:
,
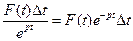а на отрезке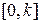 
он будет равен
.
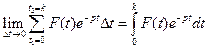В частности, если годовой доход постоянен и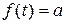 
, то его дисконтированная величина
.
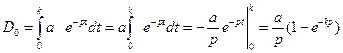Пример 7.21. Найти дисконтированный доход за три года при процентной ставке 6%, если начальные капиталовложения составляют 10 млн. грн и планируется ежегодно увеличивать капиталовложения на 1млн грн.
Решение. Очевидно, что капиталовложения определяются формулой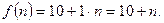 
При непрерывном дисконтировании текущая стоимость дохода равна 
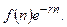Поэтому дисконтированная сумма вложений равна
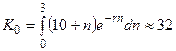млн. грн.
Пример 7.22. Кривая Лоренца — зависимость процента дохода от процента населения, который оно имеет (рис.7.6). При равномерном распределении доходов кривая Лоренца вырождается в прямую — биссектрису ОА, а поэтому площадь фигуры ОАВ между биссектрисой ОА и кривой Лоренца, отнесенная к площади треугольника ОАС (коэффициент Джини) характеризирует степень неравенства в распределении доходов населения.
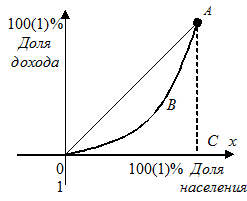
Рис. 7.6
По данным исследований в распределении доходов в одной стране кривая Лоренца ОВА может быть записана уравнением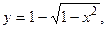 
где х — доля населения, у — доля доходов населения. Вычислить коэффициент Джини.
Решение.
,
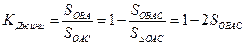поскольку 
то
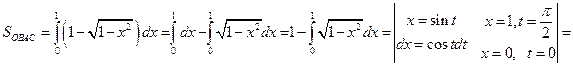
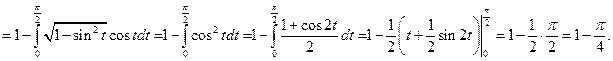Отсюда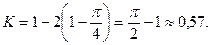 
Достаточно высокое значение K показывает неравномерное распределение доходов среди населения в государстве.
Пример 7.23. Численность населения определяется формулой 
, где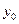 
— число жителей в начальный момент времени, 
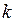— коэффициент прироста, 
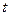— число лет. Потребление некоторого продукта в единицу времени пропорционально числу жителей и коэффициент пропорциональности равен 
. В этом случае функция «потребления»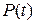 
имеет вид 
. Найти объем потребления этого продукта на промежутке от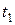 
до 
.
Решение. На малом промежутке времени от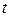 
до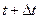 
количество жителей можно считать постоянным и в этом случае требуемое количество продукта
.
Тогда на промежутке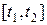 
.
Пример 7.24. В 1996 году население района было 120 тыс. человек, за 5 лет выросло до 132 тыс. человек. Найдем коэффициент прироста населения .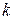
Решение. По условию 
. Следовательно,
,
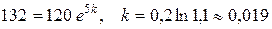т.е.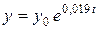 
и для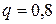 
за 5 лет необходимое количество продукта
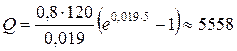(ед.)
ДВОЙНОЙ ИНТЕГРАЛ
Понятие двойного интеграла
По аналогии с интегралами одной переменной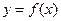 
можно построить интегральное исчисление функций нескольких переменных. Соответствующие интегралы называются кратными интегралами.
Пусть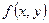 
— любая функция двух переменных, непрерывная в некоторой области D , ограниченной замкнутой линией. Разобьем область D на некоторое число n областей произвольной формы и будем называть их частичными областями. Пронумеровав частичные области в каком-нибудь порядке, обозначим их через 
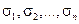, а их площади — через 
.
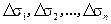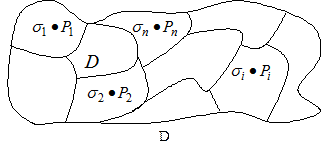
Рис.7.7
В каждой частичной области выберем по произвольной точке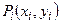 
и составим сумму
, (7.19)
где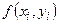 
— значение функции в точке 
.
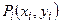Сумма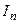 
в (7.19) называется n -ой интегральной суммой для функции 
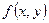в области D, соответствующей данному разбиению этой области на n частичных областей.
Диаметром области называется наибольшее расстояние между точками ее границы.
Определение 7.5. Двойным интегралом от функции 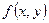по области D называется предел, к которому стремится последовательность n-ых интегральных сумм при стремлении к нулю наибольшего диаметра частичных областей.
Записывается это следующим образом:
.
Здесь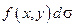 
— подынтегральное выражение, 
— подынтегральная функция, 
— элемент площади, D — область интегрирования, 
— переменные интегрирования.
Теорема существования двойного интеграла. Если функция 
непрерывна в ограниченной области D (граница которой состоит из конечного числа непрерывных линий, уравнения которых могут быть заданы в виде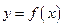 
или 
), то ее n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей. Этот предел, т. е. двойной интеграл не зависит от способа разбиения области D на частичные области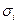 
и от выбора в них точек .
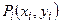Решение.
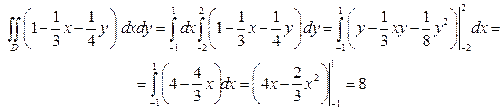
или
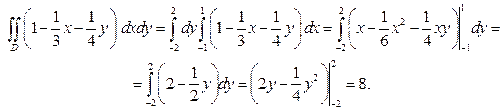
Пример 7.26. Вычислить 
, где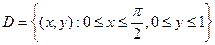 
.
Решение.
.
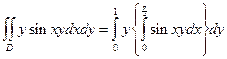Вычислим однократный интеграл
,
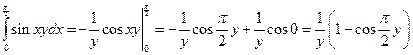затем подставим
.
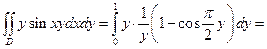
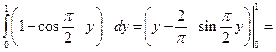
Пример 7.27. Найти двойной интеграл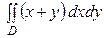 
по области D , ограниченной линиям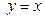и 
и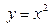 
.
Решение.
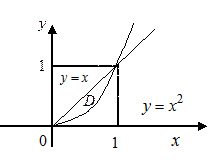
Рис. 7.10
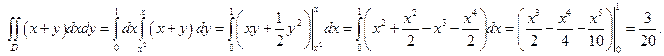
ЛИТЕРАТУРА
Для содержательных модулей
1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.
Лекция 14
Определённый интеграл. Теорема Ньютона-Лейбница. Методы интегрирования определённого интеграла.
Вопросы:
1. Понятие определённого интеграла.
2. Теорема о среднем значении.
3. Формула Ньютона-Лейбница.
4. Замена переменной в определённом интеграле.
5. Интегрирование по частям в определённом интеграле.
6. Несобственные интегралы первого и второго рода.
7. Вычисление площадей плоских фигур.
8. Вычисление объёмов тел вращения.
9. Экономические приложения определённого интеграла.
10. Понятие двойного интеграла.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Дата: 2018-11-18, просмотров: 616.
