Вычисление определенного интеграла по определению очень сложно и реально может быть проведено для двух-трех простейших функций. Хотя из данного определения не следует, что между неопределенным и определенным интегралами есть какая-либо зависимость, на самом деле они очень тесно связаны.

Теорема. Если функция 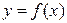 непрерывна на 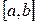, то

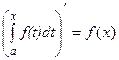                                           (7.5)

для всех 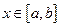 (по свойству 12).

Например,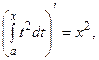

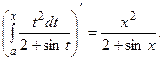
Доказательство.

Обозначим 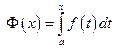. Нужно доказать, что 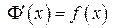. Для этого применим определение производной. Пусть  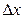— приращение аргумента. Тогда

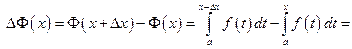
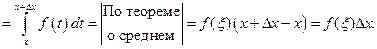
Теперь 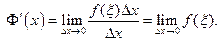 Функция  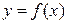непрерывна в точке х, поэтому  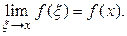Наконец  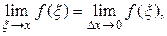так как ξ лежит между х и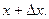

Из этой теоремы легко получить формулу для вычисления определенного интеграла. По доказанной теореме 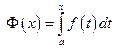 — первообразная для функции  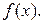Поэтому  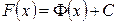— произвольная первообразная для  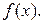Получим:

.

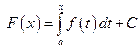Найдем постоянную С.

.

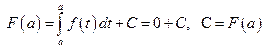Следовательно,

.

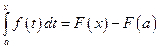Отсюда получаем формулу, называемую формулой Ньютона-Лейбница:

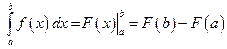,                                           (7.6)

где 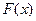 — некоторая первообразная для 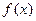, т.е. .

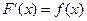Пример 7.1. Вычислить .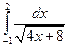

Решение.

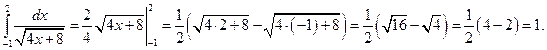
Пример 7.2. Вычислить .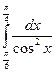

Решение.

.

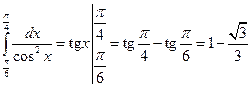Замена переменной в определенном интеграле

Теорема.

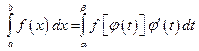,                                      (7.7)

где 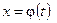 — функция, непрерывная вместе со своей производной  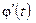на отрезке 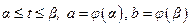, а 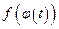 — функция, непрерывная на [α,β].

Доказательство. Пусть 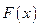 — первообразная для функции  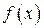на отрезке 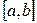. Тогда  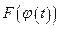— первообразная функции  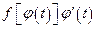на [α,β]. Действительно  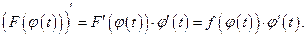Применяя дважды формулу Ньютона — Лейбница, получаем

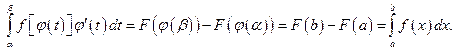
Замечание. Если 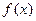 — нечетная функция, т. е. 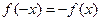, то 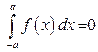. Если  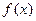— четная функция, т. е. 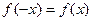, то .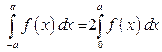

Пример 7.3. Вычислить .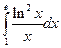

Решение. Положим 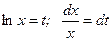; если 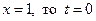; если 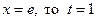. Тогда

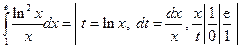
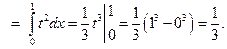
Пример 7.4. Вычислить .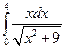

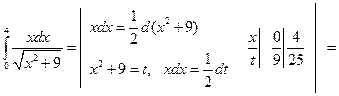
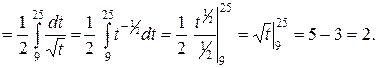
Пример 7.5. Вычислить .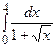

Решение. Положим 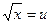. Тогда 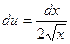, откуда 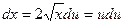. Когда переменная х изменяется от 0 до 4, то переменная 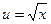изменяется от 0 до 2. Таким образом, после замены переменной у определенного интеграла изменяются пределы интегрирования. Итак, имеем

.

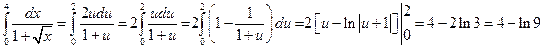Замечание. Отсюда видно, что разница в применении замены переменной в неопределенном и определенном интеграле состоит в том, что во втором случае не приходится возвращаться к старой переменной, так как при замене переменной изменяются также и пределы интегрирования.

Интегрирование по частям в определенном интеграле

Теорема.

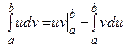,                                         (7.8)

где 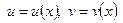 — непрерывно дифференцируемые функции на отрезке [а,b].

Доказательство. Применим формулу Ньютона — Лейбница к равенству

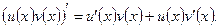 Получим

.

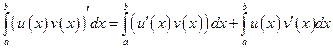Отсюда 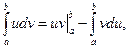 т.к. по определению дифференциала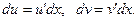

Пример 7.6. Вычислить .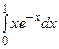

Решение. Воспользуемся методом интегрирования по частям. Положим 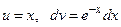, откуда 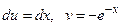. Тогда

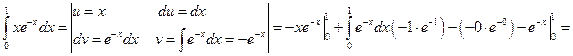
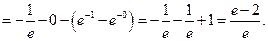
Пример 7.7.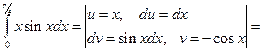

.

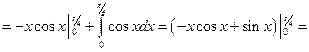
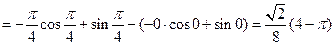Пример 7.8. Вычислить .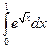

Решение. Сначала воспользуемся методом замены переменных, затем проинтегрируем полученный интеграл по частям.

.

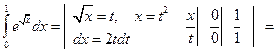
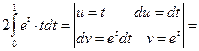
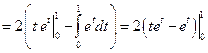
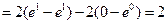НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ