Первоначально понятие определенного интеграла было дано на примере вычисления площади некоторой достаточно простой плоской фигуры — криволинейной трапеции, ограниченной снизу отрезком  оси
оси 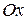 , сверху — непрерывной кривой
, сверху — непрерывной кривой 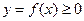 , с боков отрезками прямых
, с боков отрезками прямых 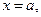
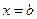 (рис.7.1). Эта площадь
(рис.7.1). Эта площадь 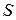 выражается интегралом
выражается интегралом
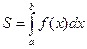 . (7.15)
. (7.15)
Площадь фигуры, ограниченной двумя кривыми 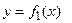 и
и 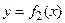
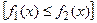 и двумя прямыми
и двумя прямыми 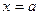 и
и 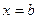 находится по формуле
находится по формуле
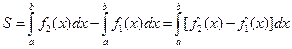 . (7.16)
. (7.16)
Эта формула верна при любом расположении относительно оси 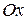 графиков функций
графиков функций 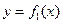 и
и 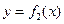 .
.
Пример 7.13. Вычислить площадь фигуры, ограниченной кривыми 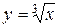 и
и 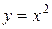 .
.
Решение. Находим точки пересечения этих кривых 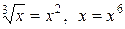 , откуда
, откуда 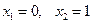 . Следовательно,
. Следовательно,
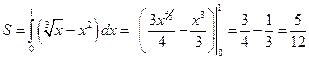 (кв. ед.).
(кв. ед.).
Пример 7.14. Найти площадь фигуры D, ограниченной линиями 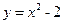 и
и 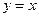 (рис.7.3).
(рис.7.3).
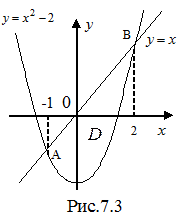 Решение. Найдем координаты точек пересечения параболы
Решение. Найдем координаты точек пересечения параболы 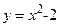 и прямой
и прямой 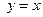 , решив систему этих уравнений: А(-1; -1) и В(2; 2). На отрезке
, решив систему этих уравнений: А(-1; -1) и В(2; 2). На отрезке
[-1, 2] выполнено неравенство 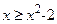 . Воспользуемся формулой (7.16), где
. Воспользуемся формулой (7.16), где 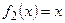 ,
, 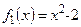 . Абсциссы точек А и В пересечения наших линий зададут пределы интегрирования.
. Абсциссы точек А и В пересечения наших линий зададут пределы интегрирования.
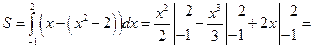
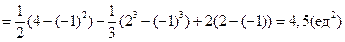 .
.
Пример 7.15. Найти площадь фигуры, ограниченной линией 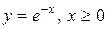 .
.
Решение.
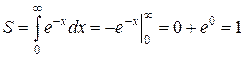 (кв. ед.).
(кв. ед.).
Вычисление объемов тел вращения
Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой 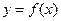 , осью Оx и двумя вертикалями
, осью Оx и двумя вертикалями 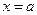 и
и 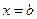 , вокруг оси Оx, выражается формулой:
, вокруг оси Оx, выражается формулой:
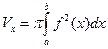 . (7.17)
. (7.17)
Если тело получается от вращения непрерывной неотрицательной функции 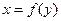 ,
, 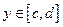 вокруг оси Оy, то его объем вычисляется по формуле:
вокруг оси Оy, то его объем вычисляется по формуле:
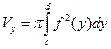 . (7.18)
. (7.18)
Пример 7.16. Вычислить объемы тел, образуемых вращением фигуры, ограниченной одной полуволной синусоиды 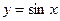 и отрезком
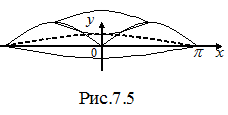
и отрезком 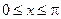 оси Оx вокруг: а) оси Оx (рис. 7.4) и б) оси Oy (рис. 7.5).
оси Оx вокруг: а) оси Оx (рис. 7.4) и б) оси Oy (рис. 7.5).
Решение.
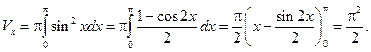
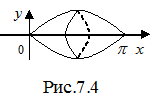
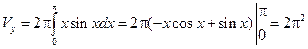 .
. 
Пример 7.17. Найти объем тела вращения относительно оси 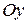 фигуры, ограниченной линиями
фигуры, ограниченной линиями 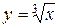 и
и 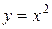 .
.
Решение. Необходимо преобразовать функции к виду 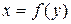 :
: 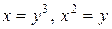 . Точки пересечения этих кривых
. Точки пересечения этих кривых 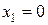 и
и 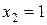 . Тогда
. Тогда
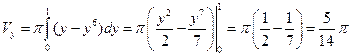 (куб. ед.).
(куб. ед.).
Пример 7.18. Найти объем тела вращения фигуры, образованной линией 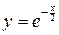 , относительно ее асимптоты при
, относительно ее асимптоты при 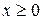 .
.
Решение. Поскольку 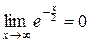 , то уравнение горизонтальной асимптоты
, то уравнение горизонтальной асимптоты 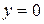 и необходимо использовать формулы объема тела вращения относительно оси
и необходимо использовать формулы объема тела вращения относительно оси 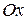 :
:
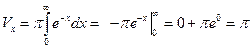 (ед. куб.).
(ед. куб.).
7.4. ЭКОНОМИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
Пример 7.19. В задаче 2 (п. 7.1.1) потребление электроэнергии можно рассматривать как кусочно-непрерывную, ограниченную на 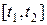 функцию. Поэтому:
функцию. Поэтому:
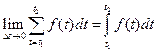 .
.
Пример 7.20. Предположим, что годовой доход 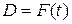 есть функция времени
есть функция времени 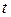 . Пусть удельная норма процента равна
. Пусть удельная норма процента равна 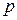 и проценты исчисляются непрерывно. Определить дисконтированный объем дохода, полученного за
и проценты исчисляются непрерывно. Определить дисконтированный объем дохода, полученного за 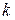 лет. (Дисконтирование — определение начальной суммы по известной конечной величине).
лет. (Дисконтирование — определение начальной суммы по известной конечной величине).
Решение. За промежуток времени от 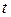 до
до 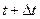 , при непрерывном начислении процентов, дисконтируемый доход составит:
, при непрерывном начислении процентов, дисконтируемый доход составит:
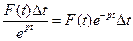 ,
,
а на отрезке 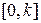 он будет равен
он будет равен
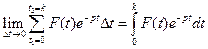 .
.
В частности, если годовой доход постоянен и 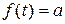 , то его дисконтированная величина
, то его дисконтированная величина
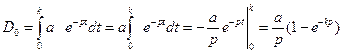 .
.
Пример 7.21. Найти дисконтированный доход за три года при процентной ставке 6%, если начальные капиталовложения составляют 10 млн. грн и планируется ежегодно увеличивать капиталовложения на 1млн грн.
Решение. Очевидно, что капиталовложения определяются формулой 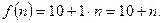 При непрерывном дисконтировании текущая стоимость дохода равна
При непрерывном дисконтировании текущая стоимость дохода равна 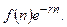 Поэтому дисконтированная сумма вложений равна
Поэтому дисконтированная сумма вложений равна
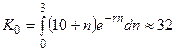 млн. грн.
млн. грн.
Пример 7.22. Кривая Лоренца — зависимость процента дохода от процента населения, который оно имеет (рис.7.6). При равномерном распределении доходов кривая Лоренца вырождается в прямую — биссектрису ОА, а поэтому площадь фигуры ОАВ между биссектрисой ОА и кривой Лоренца, отнесенная к площади треугольника ОАС (коэффициент Джини) характеризирует степень неравенства в распределении доходов населения.
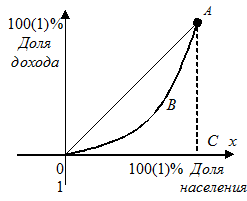
Рис. 7.6
По данным исследований в распределении доходов в одной стране кривая Лоренца ОВА может быть записана уравнением 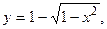 где х — доля населения, у — доля доходов населения. Вычислить коэффициент Джини.
где х — доля населения, у — доля доходов населения. Вычислить коэффициент Джини.
Решение.
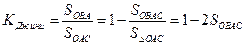 ,
,
поскольку  то
то
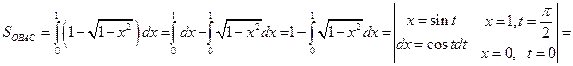
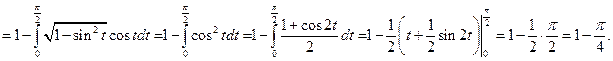 Отсюда
Отсюда 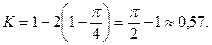
Достаточно высокое значение K показывает неравномерное распределение доходов среди населения в государстве.
Пример 7.23. Численность населения определяется формулой  , где
, где 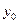 — число жителей в начальный момент времени,
— число жителей в начальный момент времени, 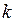 — коэффициент прироста,
— коэффициент прироста, 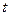 — число лет. Потребление некоторого продукта в единицу времени пропорционально числу жителей и коэффициент пропорциональности равен
— число лет. Потребление некоторого продукта в единицу времени пропорционально числу жителей и коэффициент пропорциональности равен 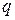 . В этом случае функция «потребления»
. В этом случае функция «потребления» 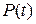 имеет вид
имеет вид 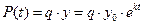 . Найти объем потребления этого продукта на промежутке от
. Найти объем потребления этого продукта на промежутке от 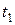 до
до 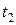 .
.
Решение. На малом промежутке времени от 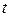 до
до 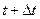 количество жителей можно считать постоянным и в этом случае требуемое количество продукта
количество жителей можно считать постоянным и в этом случае требуемое количество продукта
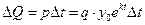 .
.
Тогда на промежутке 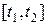
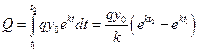 .
.
Пример 7.24. В 1996 году население района было 120 тыс. человек, за 5 лет выросло до 132 тыс. человек. Найдем коэффициент прироста населения 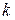 .
.
Решение. По условию  . Следовательно,
. Следовательно,
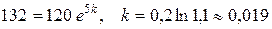 ,
,
т.е. 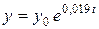 и для
и для 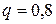 за 5 лет необходимое количество продукта
за 5 лет необходимое количество продукта
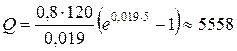 (ед.)
(ед.)
ДВОЙНОЙ ИНТЕГРАЛ
Понятие двойного интеграла
По аналогии с интегралами одной переменной 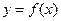 можно построить интегральное исчисление функций нескольких переменных. Соответствующие интегралы называются кратными интегралами.
можно построить интегральное исчисление функций нескольких переменных. Соответствующие интегралы называются кратными интегралами.
Пусть 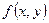 — любая функция двух переменных, непрерывная в некоторой области D , ограниченной замкнутой линией. Разобьем область D на некоторое число n областей произвольной формы и будем называть их частичными областями. Пронумеровав частичные области в каком-нибудь порядке, обозначим их через
— любая функция двух переменных, непрерывная в некоторой области D , ограниченной замкнутой линией. Разобьем область D на некоторое число n областей произвольной формы и будем называть их частичными областями. Пронумеровав частичные области в каком-нибудь порядке, обозначим их через 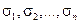 , а их площади — через
, а их площади — через 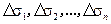 .
.
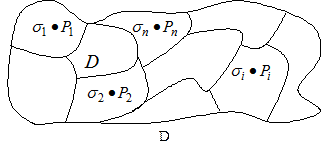
Рис.7.7
В каждой частичной области выберем по произвольной точке 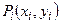 и составим сумму
и составим сумму
 , (7.19)
, (7.19)
где 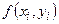 — значение функции в точке
— значение функции в точке 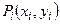 .
.
Сумма 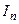 в (7.19) называется n -ой интегральной суммой для функции
в (7.19) называется n -ой интегральной суммой для функции 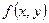 в области D, соответствующей данному разбиению этой области на n частичных областей.
в области D, соответствующей данному разбиению этой области на n частичных областей.
Диаметром области называется наибольшее расстояние между точками ее границы.
Определение 7.5. Двойным интегралом от функции 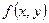 по области D называется предел, к которому стремится последовательность n-ых интегральных сумм при стремлении к нулю наибольшего диаметра частичных областей.
по области D называется предел, к которому стремится последовательность n-ых интегральных сумм при стремлении к нулю наибольшего диаметра частичных областей.
Записывается это следующим образом:
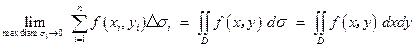 .
.
Здесь 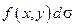 — подынтегральное выражение,
— подынтегральное выражение,  — подынтегральная функция,
— подынтегральная функция, 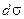 — элемент площади, D — область интегрирования,
— элемент площади, D — область интегрирования, 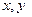 — переменные интегрирования.
— переменные интегрирования.
Теорема существования двойного интеграла. Если функция 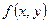 непрерывна в ограниченной области D (граница которой состоит из конечного числа непрерывных линий, уравнения которых могут быть заданы в виде
непрерывна в ограниченной области D (граница которой состоит из конечного числа непрерывных линий, уравнения которых могут быть заданы в виде 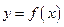 или
или  ), то ее n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей. Этот предел, т. е. двойной интеграл не зависит от способа разбиения области D на частичные области
), то ее n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей. Этот предел, т. е. двойной интеграл не зависит от способа разбиения области D на частичные области 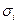 и от выбора в них точек
и от выбора в них точек 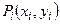 .
.
Дата: 2018-11-18, просмотров: 743.