К нахождению пределов сумм вида (7.1) приводят различные задачи. Рассмотрим такую задачу в общем виде.

Пусть на отрезке 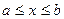 определена функция 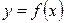. Разделим отрезок  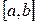произвольным образом точками  на n частей так, что  Пусть 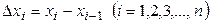 — длина этих частей, наибольшую из этих разностей в дальнейшем будем обозначать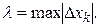  

В каждом промежутке , длиной  возьмем произвольную точку 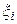 и вычислим соответствующие значения функции . Составим сумму  которая называется интегральнойсуммой для функции 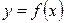 на отрезке .

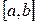Определение 7.1. Если предел последовательности интегральных сумм при стремлении к нулю длины наибольшего частичного интервала разбиения существует, конечен и не зависит от способа выбора точек  и точек 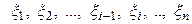, то говорят, что функция  интегрируема на .

Определение 7.2. Этот предел называют определенным интегралом от функции 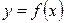 на отрезке  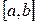и обозначают

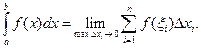                                            (7.2)

Числа a и b называются соответственно нижним и верхнимпределамиинтегрирования; 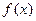 — подынтегральной функцией; 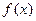 — подынтегральным выражением; отрезок 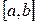— промежутком интегрирования; х — переменной интегрирования.

Теорема 1. Необходимое условие интегрируемости функции. Если функция интегрируема на отрезке , то она ограничена на .

Теорема 2. Достаточное условие интегрируемости функции. Если функция  определена на отрезке  и непрерывна на , то она интегрируема на .

Теорема 3. Кусочно-непрерывная (с конечным числом точек разрыва) и ограниченная на отрезке  функция  интегрируема.

Определения интегральной суммы и определенного интеграла естественно обобщаются на случай а > b.

Геометрический смысл определенного интеграла. Если функция 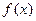 неотрицательна на отрезке 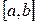, где  то  численно равен площади под кривой 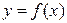 на .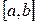

Основные свойства определенного интеграла

Замечание. В определенном интеграле не имеет значения, какой буквой обозначать переменную интегрирования:

Из определения определенного интеграла вытекают следующие его свойства.

1.                   

2.                     

3.   

4. Если , то .

5. , причем точка с может не принадлежать отрезку .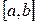

6.

7. , где С — постоянная.

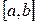8. Если функции  и  интегрируемы на отрезке на ,  и

 для всех  то

9. Оценка определенного интеграла: если  на [a,b],  то

                                    .                                      (7.3)

10. .

11. Теорема о среднем значении. Если функция 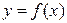 непрерывна на отрезке [a,b],  то найдется такое значение  что

                                                                                 (7.4)

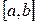Эта теорема имеет важную геометрическую интерпретацию. Пусть  на . Теорема о среднем утверждает: найдется такая точка  из отрезка 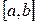 (рис. 7.2), что площадь под кривой  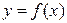равна площади прямоугольника со сторонами  и .

                                                    Рис.7.2

12. Если  и , то .