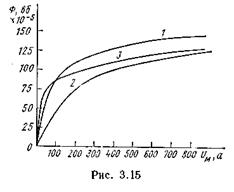
Заданы геометрические размеры магнитной цепи, кривая намагничивания и полный ток. Требуется найти поток или индукцию
Для решения задачи необходимо построить зависимость потока в функции от ∑ Hklk и на ней найти рабочую точку.
Пример 4. Найти магнитную индукцию в воздушном зазоре магнитной цепи примера 3, если lω = 350 а.
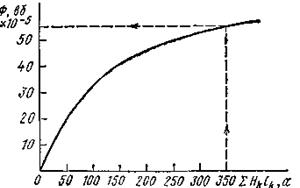
Рисунок 6.14
Решение. Задаемся значениями B0, равными 0.5; 1.1; 1.2 и 1,3 тл, и для каждого из них подсчитываем ∑Hklk так же, как в предыдущей задаче. Подсчеты сводим в табл. 6.2 

|
|
Таблица 6.2
| Bδ ,тл | 0,5 | 1,1 | 1,2 | 1,3 |
| B 1 , тл | 0,5 | 1,1 | 1,2 | 1,3 |
| B 2 , тл | 0,375 | 0,825 | 0,9 | 0,975 |
| H 1 , а/м | 50 | 460 | 700 | 1020 |
| Н2, а/м | 25 | 150 | 200 | 300 |
| Нδ, а/м | 4 105 | 8,8 105 | 9,6 105 | 10,4 105 |
| Σ Hklk, а | 58,3 | 246,3 | 333 | 450,5 |
| Ф,вб | 22,5 10-5 | 49,5 10-5 | 54 10-5 | 58,5 10-5 ■ |
По данным табл. 6.2 строим зависимость Ф = f (∑Hklk ) (рис. 6.14) и по ней находим, что при Iω = 350 а Ф = 55 10-5 вб. Следовательно,
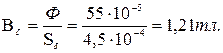
6.18. РАСЧЕТ РАЗВЕТВЛЕННОЙ МАГНИТНОЙ ЦЕПИ МЕТОДОМ ДВУХ УЗЛОВ
Ранее отмечалось, что для расчета разветвленных магнитных цепей применимы все методы, которые обсуждались ранее.
Рассмотрим расчет разветвленной магнитной цепи (см. рис. 3.12) методом двух узлов.
Пример 5. Задано: геометрические размеры в мм; кривая намагни-чивания рис. 6.9; I 1 ω 1 = 80 а, I 2 ω 2 = 300 а; зазоры δ1 = 0,05 мм и δ2 = 0,22 мм . Найти магнитные потоки в ветвях магнитной цепи.
Решение. Как и в схеме рис. 5.7, узловые точки обозначим буквами а и b. Выберем положительные направления потоков Ф1, Ф2, Ф3 к узлу а. Построим зависимость потока Ф1, от падения магнитного напряжения первой ветви UM 1 . Для этого произвольно задаемся рядом числовых значений Ф1, для каждого значения находим индукцию В1 и по кривой намагничивания напряженность Н1 на пути в стали по первой ветви.
Магнитное напряжение на первом участке
U М1 = H 1 l 1 + 0,8 106 B 1 δ 1,
где l 1 = 0,24 м - длина пути в стали по первой ветви.
Таким образом, для каждого значения потока Ф1 подсчитываем U м1 и по точкам строим зависимость Ф1 = f ( Uul ) - кривая 1 рис. 6.16.
Аналогично строим зависимость Ф2 = f ( UM 2 ) - кривая 2;
U М2 = H 2 l 2 + 0,8 106 B 2 δ 2,
где l 2 = 0,138 м - длина пути в стали по второй ветви. Кривая 3 есть зависимость Ф3 = f ( Um 3 );
U М3 = H 3 / l 3 / + H 3 // δ 3 //,
где l 3 / - 0,1м и l 3 // - 0,14м. Им соответствуют участки третьей ветви, имеющие сечения 9 и 7,5см2.
Магнитная цепь рисунок 6.12 формально аналогична нелинейной электрической цепи рисунок 5.7. Аналогом I 1 и I2 электрической цепи рис. 5.7 являются магнитные потоки Ф1 и Ф2 магнитной цепи рис. 6.12. Аналогом э.д.с. – является м. д. с. Аналогом зависимости тока в первой ветви от падения напряжения на сопротивлении первой ветви [I 1 = f ( U 1)] является зависимость магнитного потока Ф1 в первой ветви магнитной цепи от падения магнитного напряжения UMl вдоль первой ветви [Ф1 = f ( UMl )] и т. д.
Воспользуемся аналогией для определения потоков Ф1, Ф2, Ф3. С этой целью выполним графические построения, подобные построениям на рис. 5.10.
Вспомним, что кривые рис. 5.10 представляют собой зависимости токов в ветвях схемы не от падений напряжений ( U 1, U 2 , U 3 ) вдоль этих ветвей, а от напряжения Uab между двумя узлами (а и b ) схемы рис. 5.7.
В соответствии с этим введем в расчет магнитное напряжение - разность магнитных потенциалов - между узлами а и b :
UMab = φMa - φMb .
Выразим магнитный потенциал точки а (φMa) через магнитный потенциал точки b (φMb), следуя от точки b к точке а сначала по первой ветви, затем по второй и, наконец, по третьей. Для первой ветви
φMa = φMb – (H 1 l 1 + Hδ 1 δ1) + I 1 ω 1.
Здесь H 1 l 1 + Hδ 1 δ1 = UM 1 - падение магнитного напряжения по первой ветви. Знак минус перед скобкой обусловлен тем, что при перемещении согласно с направлением потока магнитный потенциал (как и электрический при перемещении по току) снижается (если бы двигались против потока, то магнитный потенциал возрастал бы и надо было ставить плюс). Плюс перед I 1 ω 1 свидетельствует о том, что при перемещении от точки b к точке а идем согласно с направлением м. д. с. Таким образом, для первой ветви
UMab = φMa - φMb =. - UM1 + I1ω1. (а)
для второй ветви (перемещаясь от b к а по потоку Ф2 и согласно с напра-влением м. д. с. I 2 ω 2 )
UMab = - UM 2 + I 2 ω 2. , (б)
для третьей ветви (в ней м. д. с. отсутствует)
UMab = - UM 1. (в)
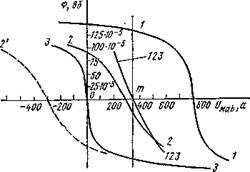
Графическое решение задачи приведено на рис. 6.16. На нем зависимость Ф1 = f (UMab) представлена кривой 1, Ф2 = f (UMab) - кривой 2; Ф3 = f (UMab) - кривой 3. Построение их производилось так же, как и построение соответствующих кривых рис. 5.10. Начало кривой /смещено в точку UMab = I 1 ω 1 = 800 а; начало кривой 2 - в точку UMab = I 1 ω 1 = 300 а. Кривая 123 представляет собой Ф1 + Ф2 + Ф3 = f (UMab). Она пересекает ось абсцисс в точке m. Проведем через точку m вертикаль и найдем потоки в ветвях:
Ф1== 126,2 10 - 5 вб;
Ф 2 = - 25 10 - 5 вб;
Ф3 = - 101,2 10 - 5 вб.
В результате расчета потоки Ф2 и Ф3 оказались отрицательными. Это означает, что в действительности они направлены противоположно положительным для них направлениям, показанным стрелками на рис. 6.12.
|
|
Рисунок 6.16
Рассмотрим, какие изменения произошли бы в построениях на рис. 6.16, если бы какая-либо из м. д. с. изменила направление на противоположное (например, в результате изменения тока в этой обмотке). Допустим, что изменилось на противоположное направление м. д. с. I 2 ω 2. В уравнение (б) м. д. с. I 2 ω 2 войдет теперь с отрицательным знаком. Это найдет свое отражение при построениях в том, что кривая 2 рис. 6.12 переместится влево параллельно самой себе так, что пересечет ось абсцисс не в точке UMab = 300 а, а в точке UMab = - 300 а (см. пунктирную кривую 2' на рис. 6.12). Кривые 1 и 3 останутся без изменений, но суммарная кривая Ф1 + Ф2 + Ф3 = f (UMab) станет иной.
Дата: 2018-11-18, просмотров: 773.