Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Глава 6

МАГНИТНЫЕ ЦЕПИ

ЭЛЕМЕНТЫ ТЕОРИИ ФЕРРОМАГНЕТИЗМА

 

Известно, что ферромагнитные тела состоят из областей самопроиз­вольного (спонтанного) намагничивания. Магнитное состояние каждой области характеризуется вектором намагниченности. Направление вектора намагниченности зависит от внутренних упругих напряжений и от кристаллической структуры ферромагнитного тела.

  Векторы намагниченности отдельных областей ненамагниченного тела направлены в различные стороны. Поэтому во внешнем по отно­шению к ферромагнитной среде пространстве намагниченность ферромагнитного тела, если оно не помещено во внешнее магнитное поле, ни в чем не проявляется. Если же ферромагнитное тело поместить о внешнее магнитное поле, то под его действием векторы намагниченности отдельных областей будут поворачиваться по внешнему полю. В результате этого индукция результирующего магнитного поля оказывается во много раз (сотни и даже сотни тысяч раз) больше, чем индукция внешнего поля до помещения в него ферромагнитного тела.

 

МАГНИТНОМЯГКИЕ И МАГНИТНОТВЕРДЫЕ МАТЕРИАЛЫ

 

Все ферромагнитные материалы можно подразделить на магнитно-мягкие и магнитнотвердые.

Магнитномягкие материалы обладают круто поднимающейся основной кривой намагничивания и относительно малыми площадями гистерезисных петель. Их применяют во всех устройствах, которые работают или могут работать при периодически изменяющемся магнитном потоке (трансформаторах, электрических двигателях и генераторах, индуктивных катушках и т. п.).

Некоторые магнитомягкие материалы, например перминвар, сплавы 68НМП и др., обладают петлей гистерезиса по форме, близкой к прямоугольной (рис. 6.3). Такие материалы получили распростра­нение в счетно-решающих устройствах и в устройствах автоматики.

в группу магнитомягких материалов входят электротехнические чали, железоникелевые сплавы типа пермаллоя и др

Магнитотвердые материалы обладают полого поднимающейся основной кривой намагничивания и большой площадью гистерезисной петли.

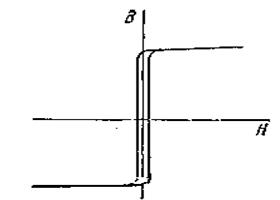В группу магнитотвердых материалов входят углеродистые стали, вольфрамовые сплавы, сплавы магнико, платинокобальтовые сплавы и др. Из магнитнотвердых материалов выполняют постоянные магниты.

                                                     

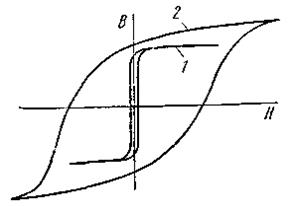
                      Рисунок 6.3                       Рисунок 6.4

 

На рис. 6.4 качественно сопоставлены гистерезисные петли для магнитномягкого материала типа пермаллоя (кривая 1) и для магнитотвердого материала (кривая 2).

 

ЗАКОН ПОЛНОГО ТОКА

 

Магнитное поле создается электрическими токами. Количественная связь между линейным интегралом от вектора напряженности магнитного поля 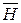 вдоль любого произвольного контура и алгебраической суммой токов 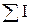, охваченных этим контуром, определяется законом полного тока

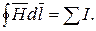                                                   (6.5)

Положительное направление интегрирования 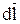 связано с поло-жительным направлением тока I правилом правоходового винта.

Закон полного тока является опытным законом. Его можно экспе-риментально проверить путем измерения 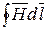 с помощью специального устройства (известного из курса физики), называемого магнитным поясом.

 

ЦЕПЕЙ С НС

В главе 5 подробно обсуждались различные приемы расчета электрических цепей с НС. Все эти методы полностью применимы и к расчету магнитных цепей, так как и магнитные и электрические цепи подчиняются одним и тем же законам - законам Кирхгофа.

Аналогом тока в электрической цепи является поток в магнитной; цепи. Аналогом э. д. с. - м. д. с. Аналогом вольтамперной характеристики нелинейного сопротивления - веберамперная характеристика участка магнитной цепи.

 

ЦЕПИ ПО ЗАДАННОМУ ПОТОКУ

Заданы конфигурация и геометрические размеры магнитной цепи, кривая (или кривые) намагничивания ферромагнитного материала и магнитный поток или индукция в каком-либо сечении. Требуется; найти м. д. с, ток или число витков намагничивающей обмотки.

 

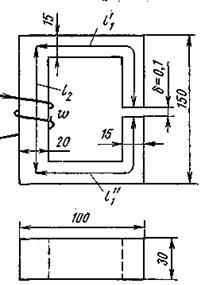
Рисунок 6.13

 

Расчет проводим в следующей последовательности:

1) разбиваем магнитную цепь на участки постоянного сечения и опре-: деляем длины l_k (в м) и площади поперечного сечения S_k (в м²) участков. Длины участков берем по средней, силовой линии;

2) исходя из постоянства потока вдоль всей цепи, по заданному потоку и сечениям S_k находим магнитные индукции на каждом участке:

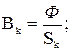
Σ H_kl_k = lω .

3) по кривой намагничивания определяем напряженности поля H_k для фер-ромагнитных участков магнитной цепи.^:

Напряженность поля в воздушном зазоре находим по формуле

H_{a /м} = 0,8 10⁶ B _тл;                                        (6.10)

4) подсчитываем сумму падений магнитного напряжения вдоль всей магнит-ной цепи ∑ H_kl_k и на основании закона полного тока приравниваем эту сумму полному току lω .

Основным допущением при расчете является то, что магнитный поток вдоль всей магнитной цепи полагаем неизменным. В действительности небольшая часть потока всегда замыкается, минуя основной путь. Например, для магнитной цепи рис. 6.6 поток, выйдя из левого сердечника, в основном направляется по пути macbn, но небольшая часть потока идет по воздуху по пути mqn.

Поток, который замыкается, минуя основной путь, называют потоком рассеяния. При малом воздушном зазоре поток рассеяния отно­сительно мал; с увеличением воздушного зазора поток рассеяния может стать соизмеримым с основным потоком.

Пример 3. Геометрические размеры магнитной цепи даны на рис. 6.13в мм; кривая намагничивания - на рис. 6.9. Найти, какой ток должен протекать по обмотке с числом витков ω = 500, чтобы магнитная индукция в воздушном зазоре В_δ = 1 тл.

Решение. Магнитную цепь разбиваем на три участка:

l₁ = l₁^/ + l₁^// = 30 см; S₁ = 4,5 см ²; l₂  = 13,5см; S₂ = 6cm^5.

     Воздушный зазор

δ = 0,01 см; S_δ = S = 4,5 см^5.

Индукция

В₁ = В_δ =1 тл.

Индукцию на участке 1₂ найдем, разделив поток Ф = B ₀ S ₀ на сечение S ₂ второго участка:

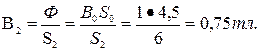
Напряженности поля на участках l ₁ и l ₂ определяем согласно кривой намагничивания (рис. 6.9) по известным значениям В₁ и В₂;

Н₁ = 300 а/м, H ₂  = 115 а/м.

     Напряженность поля в воздушном зазоре

H _δ = 0,8 10⁶      B _δ = 0,8 10⁶ - 1=8 10⁵ а/м.

Подсчитываем падение магнитного напряжения вдоль всей магнитной цепи:

ΣH_kl_k = H ₁ l ₁ + H ₂ l ₂ + H_δδ = 300 0,3 + 115 0,135 + 8 10⁵ 10 ⁴  = 185,6 а.

Ток в обмотке

 

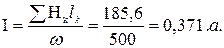
ДЛЯ МАГНИТНОЙ ЦЕПИ

 

По определению, падение магнитного напряжения (U_M = Hl ), но

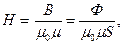                                           (6.13)

где Ф - поток; S - поперечное сечение участка.

Следовательно,

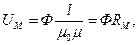                                       (6.14)

Откуда

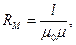                                                (6.15)

Уравнение (6.14) называют законом Ома для магнитной цепи. Это уравнение устанавливает связь между магнитным напряжением U _М и потоком Ф; R _М называют магнитным сопротивлением участка магнитной цепи. Обратную величину магнитного сопротивления называют магнитной проводимостью

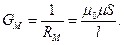                                            (6.16)

Из предыдущего известно, что веберамперная характеристика участка магнитной цепи в общем случае нелинейна. Следовательно, в общем случае R _М и G _М являются функциями магнитного потока (непостоянными величинами). Поэтому практически понятиями R _М и G _М , при расчетах используются лишь в тех случаях, когда магнитная цепь в целом или ее участок, для которых определяются R _М и G _М, не насыщены. Чаще всего это бывает, когда в магнитной цепи имеется достаточно большой воздушный зазор, спрямляющий веберамперную характеристику магнитной цепи в целом или ее участка.

Магнитное сопротивление R _М участка цепи можно сопоставить со статическим сопротивлением нелинейного сопротивления R_{c т} (см. 5.10) и так же, как последнее, R_M можно использовать при качественном рассмотрении различных вопросов, например вопроса об изменении потоков двух параллельных ветвей при изменении потока в неразветвленной части магнитной цепи (как в 5.2 по отношению к электрической цепи).

Пример 8. Найти R_M воздушного зазора постоянного магнита и по нему магнитный поток, если δ = 0,5 см , площадь поперечного сечения воздушного зазора S = 1,5 см². Магнитное напряжение на воздушном зазоре 1920 А.

Решение.

 

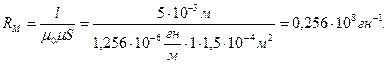
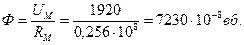
6.24. ПОЯСНЕНИЯ К ФОРМУЛЕ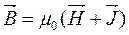

 

Из курса физики известно о связи между магнитной индукцией В, намагниченностью 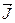 и напряженностью магнитного поля 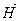. Вспомним, что контур с током i, охватывающий площадку ∆ S, создает магнитный момент  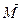=  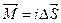(рис. 6.18, а). Величина вектора  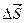численно равна площади ∆ S, а положительное направление вектора  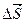связано с положительным направлением тока i правилом правоходового винта.

Ферромагнитный кольцевой сердечник, изображенный на рис. 6.18, б, имеет обмотки с числом витков ω, по которой проходит ток I. Каждая единица объема ферромагнитного материала обладает некоторым вектором намагниченности J , что при расчете можно рассматривать как результат наличия в ферромагнитном материале контуров с молекулярными токами. Эти токи показаны в сечениях сердечника на Рис. 6.18, в (намагничивающая обмотка с током I на нем не показана).

Среднюю линейную плотность молекулярного тока (а/см), приходящегося на единицу длины сердечника в направлении 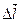, обозначим 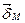. Единичный вектор, совпадающий по направлению с направлением 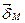, обозначим 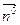. Молекулярный ток  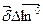In " охватывает площадку ∆ S. Положительное направление вектора  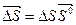связано с положительным направлением этого тока правилом правоходового винта. Через  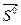обозначен единичный вектор по направлению ∆ S.

По определению, намагниченность 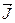 представляет собой магнитный момент синицы объема вещества. Среднюю по объему намагниченность вещества  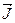можно определить путем деления магнитного момента контура с током 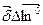,  площадку ∆ S, на объем ∆ V = ∆ l ∆ S:

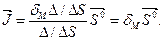
Следовательно, средняя по объему намагниченность 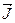 численно равна средней линейной плотности молекулярного тока и направлена по .

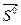Как видно из рис. 6.18, в, на участках, являющихся смежными между сосед-: ними контурами, молекулярные токи направлены встречно и взаимно компенсируют друг друга. Не скомпенсированными остаются только токи по периферийному контуру (рис. 6.18, г).

Итак, наличие областей самопроизвольной намагниченности в ферромагнитном теле при расчете можно эквивалентировать протеканием по поверхности этого тела, считая его неферромагнитным, поверхностного тока с линейной плотностью 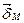, причем по модулю δ_М = J.

Запишем уравнение по закону полного тока для контура, показанного пунктиром на рис. 6.18, б. При этом учтем, что после введения поверхностного тока сердечник станет неферромагнитным и будет намагничиваться не только током I, протекающим по обмотке с числом витков ω, но и поверхностным током с линейной плотностью .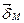

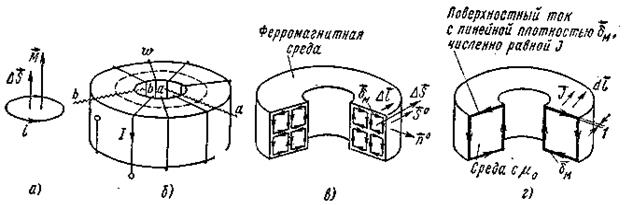
Рисунок 6.19

 

На длине dl поверхностный ток равен 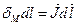. На длине всего сердечника поверхностный ток равен 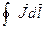. Таким образом,

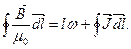
Отсюда

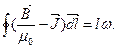
Величину 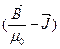     обозначают Н и называют напряженностью магнитного поля.

     В отличие от магнитной индукции 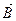 и намагниченности  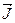напряженность поля  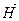не зависит от магнитных свойств намагничиваемого тела. Это и явилось основанием для того, чтобы закон полного тока для любых сред записывать в виде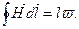

     Если ферромагнитное тело намагничено и по высоте и по толщине неравномерно. то плотность молекулярных токов смежных контуров на рис. 6.18, в будет неодинаковой, а токи на смежных между соседними контурами участках будут компенсироваться неполностью. Отсюда следует, что неравномерно намагниченное ферромагнитное тело при расчете можно заменить таким же в геометрическом смысле неферромагнитным телом, по поверхности которого течет поверхностный ток с плотностью, изменяющейся по высоте тела, а во внутренних точках тела течет объемный ток, плотность которого также изменяется от точки к точке,

 

Глава 6

МАГНИТНЫЕ ЦЕПИ

ПОДРАЗДЕЛЕНИЕ ВЕЩЕСТВ НА ДВЕ ГРУППЫ - ФЕРРОМАГНИТНЫЕ И НЕФЕРРОМАГНИТНЫЕ

 

Из курса физики известно, что все вещества по магнитным свойствам подразделяют на три группы: диамагнитные, парамагнитные и ферромагнитные. У диамагнитных веществ относительная магнитная проницаемость μ немного меньше единицы, например у висмута она равна 0,99983. У парамагнитных веществ μ немного больше единицы, например μ платины равно 1,00036. У ферромагнитных веществ (железо, никель, кобальт и их сплавы, ферриты и др.) μ много больше единицы (до 10⁴, а у некоторых материалов даже до 10⁶).

При решении большинства электротехнических задач практически достаточно подразделять все вещества не на диапара- и ферромагнитные, а на ферромагнитные и неферромагнитные. У ферромагнитных веществ ц много больше единицы, у всех неферромагнитных μ, практически равно единице.

 

               6.2. ОСНОВНЫЕ ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ МАГНИТНОЕ ПОЛЕ

 

Основными величинами, характеризующими магнитное поле, являются магнитная индукция 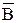 и намагниченность .

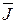Магнитная индукция 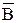 - это векторная величина, определяемая по силовому воздействию магнитного поля на ток.

     Намагниченность 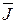 - магнитный момент единицы объема вещества.

Кроме этих двух величин, магнитное поле характеризуется напря-женностью магнитного поля .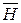

Три величины 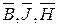 связаны друг с другом следующей зависимостью :

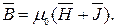                                               (6.1)

     В СИ индукция В измеряется в теслах (тл):

1 тл = 1 в-сек/м² = 1 вб/м²

или в кратных ей единицах вб/см², а в системе СГСМ - в гауссах (1 гс = 10^-8 вб/см²).

Намагниченность J и напряженность поля Н в СИ измеряют в амперах на метр (а/м), а в системе СГСМ - в эрстедах (э).

На практике индукцию В часто измеряют в единицах системы СГСМ гс, а напряженность поля H - в а/см.

     Намагниченность 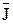 представляет собой вектор, направление которого совпадает с направлением  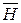в данной точке:

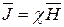.                                                      (6.2)

Коэффициент 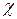 для ферромагнитных веществ является функцией Н. Подставив (6.2) в (6.1) и обозначив 1 +  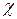= μ, получим

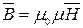,                                                        (6.3)

где μ₀ - постоянная, характеризующая магнитные свойства вакуума; μ - относительная магнитная проницаемость.

В СИ μ₀ = 4π 10^-7 гн/м = 1,256 10^-6 гн/м; в СГСМ μ₀ = 1. Для ферромагнитных веществ μ является функцией H.

Магнитный поток Ф есть поток вектора магнитной индукции через площадь S:

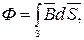                                                       (6.4)

S

где dS - элемент поверхности S.

В СИ магнитный поток измеряют в в сек или веберах (вб); в СГСМ - в максвеллах (мкс) или кратных единицах - киломаксвеллах (кмкс):

1 мкс = 10^-8 вб; 1 кмкс = 10³ мкс.

При расчетах магнитных цепей обычно используют две величины - магнитную индукцию В и напряженность магнитного поля Н.

Намагниченность J в расчетах, как правило, не используют [но при необходимости значение J, отвечающее соответствующим значениям В и Н, всегда можно найти по формуле (6.1)].