Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Свойства нелинейного сопротивления могут быть охарактеризованы либо его ВАХ, либо зависимостями его статического и дифференциального сопротивлений от тока (или напряжения).

Статическое сопротивление R _ст характеризует поведение НС в режиме неизменного тока. Оно равно отношению напряжения на НС; к протекающему по нему току:

R _ст = U / I.                                                   (5.5)

R _ст численно равно тангенсу угла а между осью ординат и прямой, идущей в точку b (рис. 5.16а) умноженному на отношение масштабов по осям m_u / m_I.

При переходе от одной точки ВАХ к соседней статическое сопротивление изменяется.

Под дифференциальным сопротивлением R _Д принято понимать отношение малого (теоретически бесконечно малого) приращения напряжения dU на НС к соответствующему приращению тока dI:

R _Д = dU / dI                                                  (5.6)

Дифференциальное сопротивление численно равно тангенсу угла в (рис. 5.16а) наклона касательной к ВАХ в рабочей точке, умноженному на m_u / m_I.. Оно характеризует поведение НС при достаточно малых отклонениях от предшествующего состояния, т. е. приращение напряжения на НС связано с приращением тока, проходящим, через него, соотношением dU = R _Д dI.

Если ВАХ НС имеет падающий участок, т. е. такой участок, на котором увеличению напряжения на ∆ U соответствует убыль тока на величину ∆I, что имеет место, например, для электрической дуги (см. ее ВАХ на рис. 5.1д), то дифференциальное сопротивление на этом участке отрицательно.

Из двух сопротивлений (R_cr и R _Д) чаще применяют R _Д. Его импользуют, например, при замене НС эквивалентным линейным сопротив­лением и э. д. с. (см. п. 5.11), а также при исследовании устойчивости режимов работы нелинейных цепей.

Пример 18. Построить кривые зависимости R_CT и R _Д. в функции от тока I для нелинейного сопротивления, ВАХ которого изображена на рис. 5.16а. Кривые построены на рис. 5.16б.

 

ЗАМЕНА НЕЛИНЕЙНОГО СОПРОТИВЛЕНИЯ ЭКВИВАЛЕНТНЫМ ЛИНЕЙНЫМ СОПРОТИВЛЕНИЕМ И Э.Д.С.

 

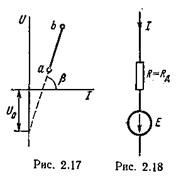
Если заранее известно, что изображающая точка будет переме­щаться лишь по определенному участку ВАХ НС и этот участок может быть с известной степенью приближения заменен прямой линией, то НС при расчете может быть заменено эквивалентным линейным сопротивлением и источником э. д. с. Положим, что рабочая точка будет перемещаться лишь по участку а b рис. 5.16, а (см. также рис. 5.17). Для этого участка

U = U ₀ + Itgβ = U ₀ + IR _Н.                                      (5.7)

Уравнению (5.7) удовлетворяет участок цепи рис. 5.18. На нем Е = - U₀ и линейное сопротивление R = R_Д.

Замена НС на линейное сопротивление и э. д. с. удобна тем, что после та-кой замены вся схема становиться линейной и ее работа может быть исследована методами, разработанными для линейных цепей. Однако приэтом необходимо внимательно следить за тем, чтобы рабочая точка не выходила за пределы линейного участка ВАХ.

Пример 19. Выразить аналитически участок ВАХ рис. 5.16а в интервале между точками а и с.

Решение. Из рис 5.16а находим U₀ = - 45В и R_Д = tg β = 220Ом. Следовательно U = -45 + 220 I.

СТАБИЛИЗАТОР ТОКА

Стабилизатором тока называют устройство, которое способно под-держивать в нагрузке неизменный ток при изменении сопротивления нагрузки и при изменении напряжения на входе всей схемы.

Стабилизацию постоянного тока можно производить с помощью различных схем. Простейшей схемой стабилизатора тока является схема рис. 5.19. В ней последовательно с нагрузкой R _Д включено НС типа бареттера Б. На рис. 5.20 приведена ВАХ бареттера 0.3Б17-35. Первая цифра означает величину тока в амперах, который бареттер способен поддерживать постоянным, цифры 17-35 показывают область изменения напряжения на бареттере в вольтах на участке бареттирования (поддержания постоянства тока).

 

 

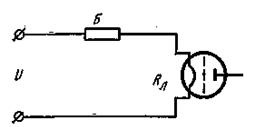
Рисунок 5.19

Пример 20. Бареттер 0.3Б17-35 используется для стабилизации тока на-кала электронной лампы. Номинальный ток накала 0,3А, напряжение 6В. Требуется найти, в каких пределах можно изменять напряжение U на входе схемы, чтобы ток нити накала лампы оставался неизменным и равным 0,3А.

 

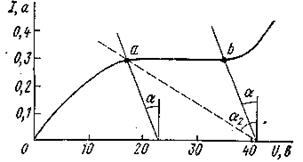
Рисунок 5.20

Решение. Находим сопротивление нити накала лампы:

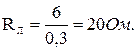
Проводим через точки а и b (рис. 5.20), ограничивающие участок бареттирования, две прямые под углом α (tgα с учетом масштабов по осям численно равен 20) к вертикали. По рис. 5.20 определяем, что напряжение U можно изменять в интервале 23-41В.

Пример 21. В схему предыдущей задачи введено последовательное сопротивление R ₁. Полагая напряжение на входе схемы неизменным и равным 41В, найти, до какого максимального значения R ₁ в схеме будет иметь место стабилизация тока.

Решение. Если R₁ = 0 и U = 41В, то рабочий режим характеризуется положением точки b(рис. 5.20). С увеличением сопротивления R ₁ рабочая точка ВАХ перемещается по направлению к точке а. В граничном режиме в точке а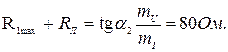

Следовательно, R_1max = 80 - 20 = 60Ом.

 

СТАБИЛИЗАТОР НАПРЯЖЕНИЯ

 

Стабилизатором напряжения называют устройство, напряжение на выходе которого U_H поддерживается постоянным или почти постоянным при изменении сопротивления нагрузки R _Н или величины напряжения U ₁ на входе устройства.

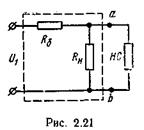
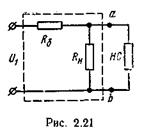
Схема простейшего стабилизатора напряжения показана на рис. 5.21. В качестве НС используется стабиловольт; R ₆ - балластное сопротивление.

 

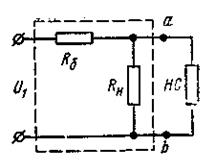
Рисунок 5.21

     На рис. 5.22 изображена ВАХ стабиловольта 150С5-30.

При анализе работы стабилизатора определяют пределы допустимых изменений U ₁ при R_n = const, а также исследуют работу стабилизатора при одновременном изменении U ₁ и  R _Н.

Для оценки качества работы стабилизатора иногда пользуются понятием коэффициента стабилизации. Под ним понимают отношение относительного приращения напряжения на входе стабилизатора (∆ U₁/U₂) к относительному приращению напряжения на выходе стабилизатора (∆ U_H/U_H).

Пример 22. В схеме рис. 5.21 R _Н = 5 ком, R ₆ = 2 ком. Характеристика стабиловольта соответствует рис. 5.25. Определить границы допустимого изменения U ₁, чтобы стабилизатор давал на выходе стабилизированное напряжение 150В.

    

 

 

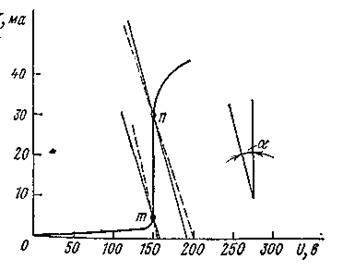
Рисунок 5.22

     Решение. Воспользуемся методом эквивалентного генератора. Разомкнем ветвь стабиловольта и найдем напряжение холостого хода:

Определим входное сопротивление линейной части схемы (рис. 5.21) по отношению к зажимам а b:

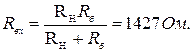
На рис. 5.22 проведем две прямые (сплошные) линии через точки m и n ВАХ стабиловольта так, чтобы тангенс угла (образованного ими с вертикалью) Умноженный на m_U / m_I равнялся R_BX = 1427 ом.

  Отрезки, отсекаемые этими прямыми на оси абсцисс, равны U_{x х .} Из рисунка находим 0,713U_min = 157B, или U_lmin = 220B. Аналогично, 0,713U_max = 192B, или U_lmax = 269B. Следовательно, напряжение U ₁ может изменяться от 220 до 269 в.

  Пример 23. На рис. 5.21 при R _б = 2кОм, характеристике стабиловольта рис. 5.22 и U ₁ = 250В определить, в каких пределах можно изменять сопротивление нагрузки R_H, чтобы стабилизатор мог выполнять свои функции по стабилизации выходного напряжения.

Решение. Воспользовавшись методом эквивалентного генера­тора, определим

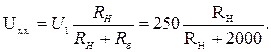
Находим

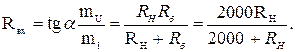
Задача сводится к определению значений R_H, при которых прямые, характеризующие R_BX, будут проходить через точки m и n ВАХ стабиловольта. В данном примере неизвестны ни тангенсы углов α, ни исходные точки на оси абсцисс, из которых должны быть проведены прямые, поэтому решаем задачу путем пробных построений. С этой целью задаемся значениями R_H, подсчитываем соответствующие им U_{x . x} и R _вх.

 

R кOм	3	4	5	6	7	8
Uх.х, B RBX, Ом	150 1200	167 1330	178 1425	187 1500	194 1555	200 1600

    

По данным таблицы проводим несколько лучей. Графически находим, что прямые (см. пунктирные прямые на рис. 5.22) пройдут через точки m и n соответственно при R_{н min} = 3,3 кОм и R_{H max} = 8 кОм.

 

Рисунок 5.23