Положим, что имеется совокупность нескольких параллельных ветвей, содержащих НС и э. д. с. (рис. 5.11). Параллельные ветви входят в состав сложной схемы, не показанной на рис. 5.11. Каковадолжна быть э. д. с. и ВАХ эквивалентного нелинейного сопротивления НСЭ участка схемы рис. 5.12, чтобы он был эквивалентен параллельным ветвям рис. 5.11?

Одна ветвь рис. 5.12 будет эквивалентной ветвям рис. 5.11 в том случае, если ток I в неразветвленной части цепи рис. 5.11 при любых значениях напряжения U_ah будет равняться току I в ветви рис. 5.15.

     Рисунок 5.11                                        Рисунок 5.12

  Воспользуемся построениями на рис. 5.10. Кривая 4 рис. 5.10 представляет собой зависимость

I ₁ + I ₂ + I ₃ = f ( U_ab )

т. е. является результирующей ВАХ трех параллельных ветвей. Такую же ВАХ должна иметь ветвь рис. 5.15. Если ток I в схеме рис. 5.12 будет равен нулю, то U_ab = Ё_э. Следовательно, Е_э на рис. 5.10 определяется напряжением U_ab, при котором кривая 4 будет пересекать ось абсцисс. Для определения ВАХ НСЭ необходимо кривую 4 рис. 5.10 зеркально отобразить относительно вертикали, проведенной через точку т. ВАХ НСЭ изображена на рис. 5.13. Важно подчеркнуть, что включение э. д. с. в параллельные ветви привело к тому, что ВАХ НСЭ стала несимметричной, несмотря на то что ВАХ нелинейных сопротивлении 1, 2, 3 в схеме рис. 5.7 были взяты симметричными.

Таким образом, изменяя э. д. с. в ветвях параллельной группы, можно изменять ее результирующую ВАХ и как бы искусственно создавать НС с самыми причудливыми ВАХ.

Рисунок 5.13

\

РАСЧЕТ НЕЛИНЕЙНЫХ ЦЕПЕЙ МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Если в сложной электрической цепи есть одна ветвь с НС, то определение тока в ней можно производить по методу эквивалентного генератора. С этой целью выделим ветвь с НС, а всю остальную линейную схему представим в виде активного двухполюсника (рис. 5.14а).

Рисунок 5.14

Как известно, схему линейного активного двухполюсника по отношению к зажимам а и b выделенной ветви можно представить в виде последовательного соединения источника э. д. с. С э. д. с., равной напряжению на зажимах ab при размыкании ветви ( U_{ab х х}) сопротивления, равного входному сопротивлению R_BX линейного двухполюсника, и сопротивления ветви ab (рис. 5.14б).

Определение тока в схеме рис. 5.14б не представляет труда и может проводиться в соответствии с п. 5.5.

Пример 17. Определить ток в ветви ab схемы рис. 5.15 по методу эквивалентного генератора при R₁ = R₀ = 2Oм, R₂ = 8Oм, R₃ =4 Oм, R₄ =6 Oм; Е = 58,4 B. ВАХ НС изображена на рис. 5.16a.

Решение. Размыкаем ветвь и определяем напряжение холостого хода:

U_ab.x.x = 8,35B.

Для подсчета входного сопротивления R _вх, линейной части схемы относительно зажимов ab необходимо преобразовать треугольник сопротивлений R ₁ , R _2, R ₀(или R ₄ , R _0, R ₃ ) (рис. 5.15б) в эквивалентную звезду (рис. 5.15в)

,

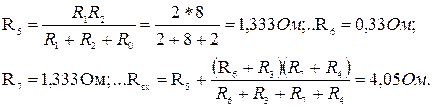
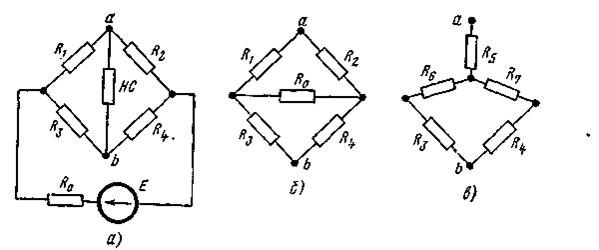
Рисунок 5.15

     Для определения тока в ветви ab (рис. 5.15) на рис. 5.16а из точки m ( Ux . x . = 8,35В проводим луч mn, угла наклона γ , Которго к вертикали (с учетом масштабов по осям абсцисс и ординат) численно равен R_BX. Точка n пересечения луча mn с ВАХ нелинейного сопротивления определяет рабочий режим схемы:

l = 0,22 а.

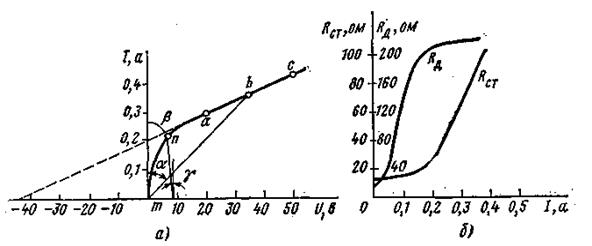
Рисунок 5.16