НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Глава 5

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

ПОСТОЯННОГО ТОКА

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Под нелинейными электрическими цепями принято понимать электрические цепи, содержащие нелинейные элементы. Нелинейные элементы подразделяют на нелинейные сопротивления, нелинейные индуктивности и нелинейные емкости.

Нелинейные сопротивления (НС) в отличие от линейных обладают нелинейными вольтамперными характеристиками. Напомним, что вольтамперная характеристика (ВАХ) - это зависимость тока, протекающего через сопротивление, от напряжения на нем. Нелинейные сопротивления могут быть подразделены на две большие группы: неуправляемые и управляемые НС. В управляемых НС в отличие от неуправляемых, кроме основной цепи, как правило, есть еще по крайней мере одна вспомогательная, или управляющая цепь, воздействуя на ток или напряжение которой можно деформировать ВАХ основной цепи. В неуправляемых НС ВАХ изображается одной кривой, а в управляемых - семейством кривых.

В группу неуправляемых НС входят лампы накаливания, электрическая дуга, бареттер, газотрон, стабиловольт, тиритовые и вилитовые сопротивления, полупроводниковые выпрямители (диоды) и некоторые другие НС.

В группу управляемых НС входят трех- (и более) электродные лампы, полупроводниковые триоды (транзисторы), тиристоры и другие элементы.

ВОЛЬТАМПЕРНЫЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ СОПРОТИВЛЕНИЙ

На рис. 5.1 изображено одиннадцать типов наиболее часто встре-чающихся вольтамперных характеристик неуправляемых НС.

ВАХ типа рис. 5.1а имеют, например, лампы накаливания с металлической нитью. Чем больше протекающий через нить ток, тем нить сильнее нагревается и тем больше становится ее сопротивление.

Если величину, откладываемую по оси абсцисс, обозначить через х, а величину, откладываемую по оси ординат, - через f ( x ), то характеристика типа «а» подчиняется условию

f ( x ) = - f (- х).

Нелинейные сопротивления, для которых выполняется это условие, называют нелинейными сопротивлениями с симметричной вольтамперной характеристикой.

ВАХ типа рис. 5.1б обладают тиритовые и вилитовые сопротивления, некоторые типы терморезисторов и лампы накаливания с угольной нитью.

Основу тирита и вилита составляют мелкоизмельченный графит и карборунд. После соответствующей технологической обработки эту массу прессуют в виде дисков и запекают. Вилитовые и тиритовые НС используют в нелинейных мостовых схемах автоматики, применяемых, например, в качестве индикаторов отклонения напряжения генераторов от номинала. Их широко используют в защитных устройствах при передаче энергии высокого напряжения. Для данной группы характерно то, что с увеличением протекающего тока сопротивление их уменьшается. ВАХ их симметрична.

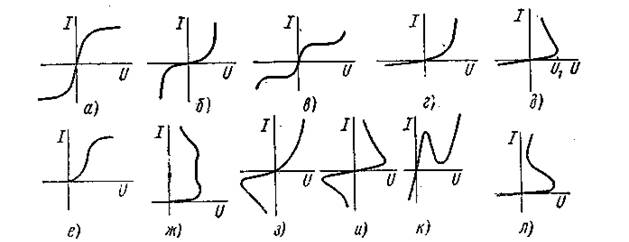
Рисунок 5.1

ВАХ типа рис. 5.1б обладает, например, бареттер. Бареттер выполняют в виде спирали из стальной проволоки, помещенной в стеклянный сосуд, заполненный водородом при давлении порядка 80 мм рт. ст. В определенном диапазоне изменения тока ВАХ бареттера расположена почти горизонтально. Бареттер используют для стабилизации тока накала электронных ламп при изменении напряжения питания.

ВАХ типа рис. 5.1в также симметрична.

ВАХ типа рис. 5.1г в отличие от предыдущих несимметрична. Ею обладают полупроводниковые выпрямители (меднозакисные, селеновые, кремниевые, германиевые), очень широко применяемые для преобразования переменного тока в постоянный. Они способны пропускать ток практически только в одном, проводящем, направлении. Широко используют их также в различных датчиках и преобразоваелях устройств автоматики.

ВАХ типа5.1д имеют электрическая дуга с разнородными электродами, газотрон и некоторые типы терморезисторов. Если напряжение повышать, начиная с нуля, то сначала ток растет, но остается весьма малым, после достижения напряжения U₁ (напряжение зажигания) происходит резкое увеличение тока в цепи и снижение напряжения на электрической дуге или газотроне. Для верхнего участка ВАХ приращению тока соответствует убыль напряжения нелинейном сопротивлении.

Участок ВАХ типа верхнего участка кривой рис. 5.1д называют падающим участком вольтамперной характеристики.

Электрическую дугу широко применяют при сварке металлов, в электротермии (в дуговых электропечах), а также в качестве мощного источника электрического освещения, например в прожекторах.

Газотрон представляет собой лампу с двумя электродами, заполненную благородным газом или парами ртути.

ВАХ типа рис. 5.1е имеет двухэлектродная выпрямительная лампа - кенотрон. По нити накала лампы пропускают ток. Этот ток разогревает катод (один из двух электродов лампы) до высокой температуры, в результате чего с поверхности катода начинается термоэлектронная эмиссия. Под действием электрического поля поток электронов направляется ко второму, холодному, электроду - аноду. В начальной части ВАХ(рис. 5.1е) зависимость тока от напряжения подчиняется закону трех вторых i = au ^3/5. ВАХ кенотрона несимметрична, это объясняется тем, что поток электронов направляется с катода на анод только в том случае, если анод положителен по отношению к катоду.

ВАХ типа рис. 5.1ж обладают лампы с тлеющим разрядом. К числу их относятся стабиловольты и неоновые лампы. При тлеющем разряде благородный газ, которым заполнена лампа (неон, аргон и др.), светится. ВАХ типа рис. 5.1ж свидетельствует о том, что в определенном диапазоне значений токов напряжение на лампе остается практически неизменным.

Некоторые типы точечных германиевых и кремниевых выпрямителей имеют ВАХ типа рис. 5.1з.

Электрическая дуга между электродами, выполненными из одного и того же материала и находящимися в одинаковых условиях, имеет ВАХ типа рис. 5.1и.

ВАХ четырехслойного германиевого (кремниевого) диода - тринистора - изображена на рис. 5.1л;

ВАХ туннельного диода - на рис. 5.1к .

В качестве управляемых нелинейных сопротивлений широко применяют полупроводниковые триоды (транзисторы), тиристоры и трехэлектродные электронные лампы.

Рисунок 5.2

ного сопротивления - прямая линия. ВАХ всей цепи, т. е. зависимость тока в цепи от суммы падений напряжений на НС и R, обозначена через I = f ( U_HC + U_R ). Расчет основывается на законах Кирхгофа. Обсудим два способа расчета. Первый способ иллюстрируется рис. 5.2б, второй - рис. 5.2в.

При расчете цепи по первому способу строим результирующую ВАХ всей пассивной части схемы, исходя из того, что при последовательном соеди-

нении через НС и R течет одинаковый ток. Для построения результирующей ВАХ задаемся произвольным током - точкой m, проводим через нее (см. рис. 5.2б) горизонталь и складываем отрезок mn, равный напряжению на НС, с отрезком mp, равным напряжению на R:

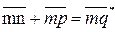Точка q принадлежит результирующей ВАХ всей схемы. Аналогично строят и другие точки результирующей ВАХ. Определение тока в цепи при заданной э. д. с. Е производят графически по результирующей ВАХ. (рис. 5.2б). С этой целью следует заданную величину э. д. с. Е отложить по оси абсцисс и через полученную точку на оси абсцисс провести вертикаль до пересечения с результирующей в. а. х. в точке q. Ордината точки q равна искомому току.

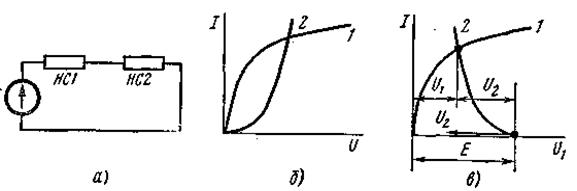
Рисунок 5.3

При расчете цепи по второму способу нет необходимости строить результирующую ВАХ всей пассивной части схемы. Учитывая, что уравнение IR + U_HC = Е в координатах I и U_HC представляет собой уравнение прямой, проходящей через точки I = E / R ; U = U_HC =0; I = 0; U_HC = U = Е, проводим на рис. 5.2 в эту прямую. Тангенс угла а наклона ее к вертикали, умноженный на отношение т_и1т, масштабов по осям, численно равен R. Точка пересечения прямой с ВАХ. НС определяет режим работы цепи. Действительно, для этой точки ток, проходящий через НС и через R, одинаков, а сумма падений напряжений U_HC + U_R = Е. При изменении э. д. с. со значения Е до Е₁ прямую

I = f ( U_R ) надо переместить параллельно себе так, чтобы она исходила из точки I = 0, U = Е₁ (пунктирная прямая на рис. 5.2в).

Аналогично рассчитывают цепи при последовательном соединении двух и большего числа НС. В этом случае сначала находят ВАХ. двух НС, затем трех и т. д.

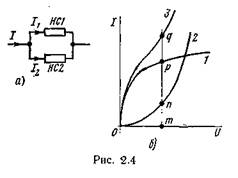
Обсудим применение второго способа для расчета цепи рис. 5.3а с двумя различными НС; ВАХ НС₁ и НС₂ изображены на рис. 5.3б. Так как НС₂ имеет нелинейную ВАХ, то вместо прямой I = f ( U_R ), как это было на рис. 5.2в, теперь надо нанести нелинейную зависимость I = f ( U ₂ ). Начало ее (рис. 5.3в) расположено в точке I = 0, U ₁ = E. Отсчет положительных значений U ₂ производится влево от этой точки. Так как положительные значения U_HC ₂ на рис. 5.3б откладываются вправо от начала координат, а на рис. 5.3в – влево, то кривая I = f ( U ₂ ) рис. 5.3в представляет собой зеркальное отображение кривой 2 рис. 5.3б относительно вертикальной оси, проведенной через точку U ₁ = Е.

Рисунок 5.4

5.6. ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ НЕЛИНЕЙНЫХ СОПРОТИВЛЕНИЙ

На рис. 5.5 изображена схема последовательного соединения НСЗ и двух параллельно соединенных НС1 и НС5. Требуется найти токи в ветвях схемы.

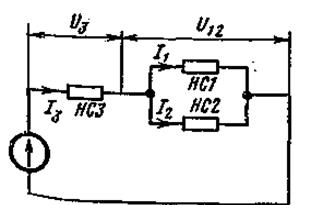
Рисунок. 5.5

Заданы ВАХ нелинейных сопротивлений (кривые 1, 2, 3, рис. 5.6) и э. д. с. Е. Сначала строим ВАХ параллельного соединения в соответствии с п. 5.5 (кривая 1 + 2 на рис. 5.6). После этого цепь сводится к последовательному соединению НСЗ и НС, имеющего ВАХ 1 + 5.

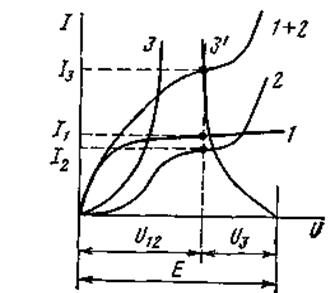
Рисунок 5.6

Применяем второй способ построения, описанный в п. 5.5. Кривая 3^/ рис. 5.6 представляет собой ВАХ НСЗ, зеркально отраженную _fотносительно вертикали, проведенной через точку U = Е. В точкепересечения кривой 3' с кривой 1+2 удовлетворяется второй закон Кирхгофа U ₃ + U ₁₂ = Е. Сумма токов I ₁ и I ₂ равна току I ₃.

Рисунок 5.7

Каждый из токов является нелинейной функцией падения напряжения на своем НС. Так, I ₁ является функцией U ₁, I ₂ - функцией _U₂ и I ₃ - функцией U ₃.

Выразим все токи в функции не от различных переменных (U_lt U₂, U₃), а в функции одного переменного - напряжения U_ab между двумя узлами:

U₁ = E₁- U_ab; (5.2)

U₂ = E₂- U_ab; (5.3)

U ₃ = E ₃ - U_ab. (5.4)

Таким образом, возникает задача о перестройке кривой I ₁ = f ( U ₁ ) в кривую I ₁ = f ( U_ab ), кривой I ₂ = f ( U ₂ ) - в кривую I ₂ = f ( U_ab ) и т. д. На рис. 5.9 показано, как из кривой I ₁ = f ( U ₁ ) (рис. 5.8а) получить кривую I ₁ = f ( U_ab ) - точки соответственно обозначены одинаковыми цифрами.

Для точки 5 кривой рис. 5.8а I ₁ = 0 и U ₁ = 0; при этом U_ab = Е₁ (формула (5.2)], т. е. начало кривой I ₁ = f ( U_ab ) сдвинуто в точку U_ab = Е₁.

Росту U ₁ при U ₁ > 0 соответствует убыль U_ab. Для точки 2 при значении U = Е_г напряжение U _аЬ = 0. Росту U ₁ при U ₁ < 0 отвечает рост U_atb причем U_ab > Е₁.

На основании изложенного рекомендуется поступать следующим образом:

1) сместить кривую I ₁ = f ( U ₁ ) параллельно самой себе так, чтобы ее начало находилось в точке U_ab = Е₁. Кривая, полученная в результате переноса. представлена пунктиром на рис. 5.9;

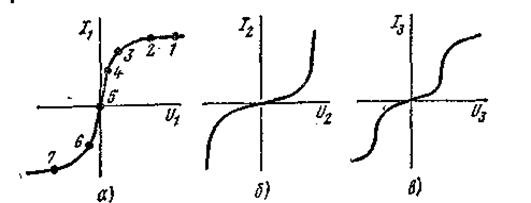
Рисунок 5.8

2) провести через точку U_ab = Е₁ вертикаль и зеркально отразить пунктирную кривую относительно вертикали.

Аналогичным образом производится перестройка кривых и для других ветвей схемы. Нанесем кривые I ₁ = f ( U_ab ), I ₂ = f ( U_ab ) и I ₃ = f ( U_ab ) на одном ри-сунке (на рис. 5.10 кривые 1, 2, 3) а построим кривую I ₁ + I ₂ + I ₃ = f ( U_ab ) (на рис. 5.10 кривая 4), просуммировав ординаты кривых 1, 2, 3.

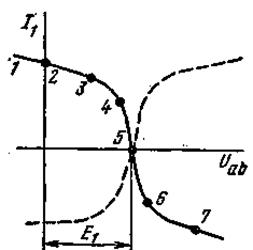
Рисунок 5.9

Точка m пересечения кривой 4 с осью абсцисс дает значение U_ab, при котором удовлетворяется уравнение (5.1). Восставим в этой точке перпендикуляр к оси абсцисс. Ординаты точек пересечения перпендикуляра с кривыми 1, 2, 3 дадут соответственно токи I _1, I ₂ и I ₃ по величине и по знаку.

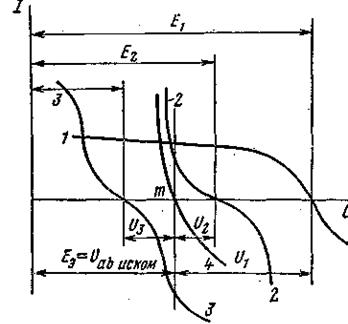
Рисунок 5.10

Рисунок 5.13

Рисунок 5.14

Как известно, схему линейного активного двухполюсника по отношению к зажимам а и b выделенной ветви можно представить в виде последовательного соединения источника э. д. с. С э. д. с., равной напряжению на зажимах ab при размыкании ветви ( U_ab _х _х) сопротивления, равного входному сопротивлению R_BX линейного двухполюсника, и сопротивления ветви ab (рис. 5.14б).

Определение тока в схеме рис. 5.14б не представляет труда и может проводиться в соответствии с п. 5.5.

Пример 17. Определить ток в ветви ab схемы рис. 5.15 по методу эквивалентного генератора при R₁ = R₀ = 2Oм, R₂ = 8Oм, R₃ =4 Oм, R₄ =6 Oм; Е = 58,4 B. ВАХ НС изображена на рис. 5.16a.

Решение. Размыкаем ветвь и определяем напряжение холостого хода:

U_ab_._x_._x = 8,35B.

Для подсчета входного сопротивления R _вх, линейной части схемы относительно зажимов ab необходимо преобразовать треугольник сопротивлений R ₁ , R _2, R ₀(или R ₄ , R _0, R ₃ ) (рис. 5.15б) в эквивалентную звезду (рис. 5.15в)

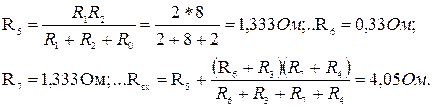
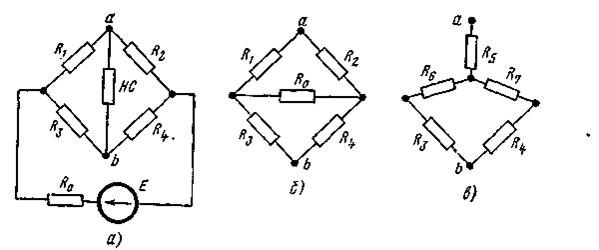
Рисунок 5.15

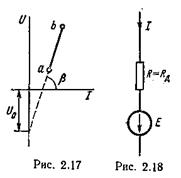
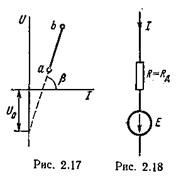
Для определения тока в ветви ab (рис. 5.15) на рис. 5.16а из точки m ( Ux . x . = 8,35В проводим луч mn, угла наклона γ , Которго к вертикали (с учетом масштабов по осям абсцисс и ординат) численно равен R_BX. Точка n пересечения луча mn с ВАХ нелинейного сопротивления определяет рабочий режим схемы:

l = 0,22 а.

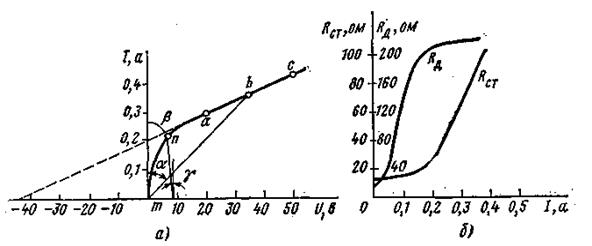
Рисунок 5.16

СТАБИЛИЗАТОР ТОКА

Стабилизатором тока называют устройство, которое способно под-держивать в нагрузке неизменный ток при изменении сопротивления нагрузки и при изменении напряжения на входе всей схемы.

Стабилизацию постоянного тока можно производить с помощью различных схем. Простейшей схемой стабилизатора тока является схема рис. 5.19. В ней последовательно с нагрузкой R _Д включено НС типа бареттера Б. На рис. 5.20 приведена ВАХ бареттера 0.3Б17-35. Первая цифра означает величину тока в амперах, который бареттер способен поддерживать постоянным, цифры 17-35 показывают область изменения напряжения на бареттере в вольтах на участке бареттирования (поддержания постоянства тока).

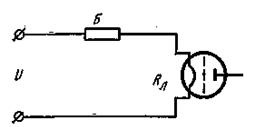
Рисунок 5.19

Пример 20. Бареттер 0.3Б17-35 используется для стабилизации тока на-кала электронной лампы. Номинальный ток накала 0,3А, напряжение 6В. Требуется найти, в каких пределах можно изменять напряжение U на входе схемы, чтобы ток нити накала лампы оставался неизменным и равным 0,3А.

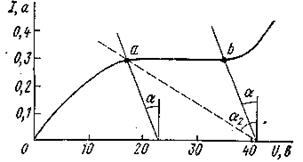
Рисунок 5.20

Решение. Находим сопротивление нити накала лампы:

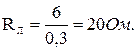
Проводим через точки а и b (рис. 5.20), ограничивающие участок бареттирования, две прямые под углом α (tgα с учетом масштабов по осям численно равен 20) к вертикали. По рис. 5.20 определяем, что напряжение U можно изменять в интервале 23-41В.

Пример 21. В схему предыдущей задачи введено последовательное сопротивление R ₁. Полагая напряжение на входе схемы неизменным и равным 41В, найти, до какого максимального значения R ₁ в схеме будет иметь место стабилизация тока.

Решение. Если R₁ = 0 и U = 41В, то рабочий режим характеризуется положением точки b(рис. 5.20). С увеличением сопротивления R ₁ рабочая точка ВАХ перемещается по направлению к точке а. В граничном режиме в точке а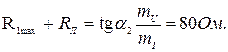

Следовательно, R₁_max = 80 - 20 = 60Ом.

СТАБИЛИЗАТОР НАПРЯЖЕНИЯ

Стабилизатором напряжения называют устройство, напряжение на выходе которого U_H поддерживается постоянным или почти постоянным при изменении сопротивления нагрузки R _Н или величины напряжения U ₁ на входе устройства.

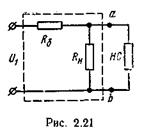
Схема простейшего стабилизатора напряжения показана на рис. 5.21. В качестве НС используется стабиловольт; R ₆ - балластное сопротивление.

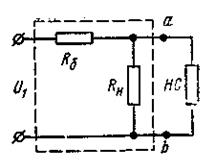
Рисунок 5.21

На рис. 5.22 изображена ВАХ стабиловольта 150С5-30.

При анализе работы стабилизатора определяют пределы допустимых изменений U ₁ при R_n = const, а также исследуют работу стабилизатора при одновременном изменении U ₁и R _Н.

Для оценки качества работы стабилизатора иногда пользуются понятием коэффициента стабилизации. Под ним понимают отношение относительного приращения напряжения на входе стабилизатора (∆ U₁/U₂) к относительному приращению напряжения на выходе стабилизатора (∆ U_H/U_H).

Пример 22. В схеме рис. 5.21 R _Н = 5 ком, R ₆ = 2 ком. Характеристика стабиловольта соответствует рис. 5.25. Определить границы допустимого изменения U ₁, чтобы стабилизатор давал на выходе стабилизированное напряжение 150В.

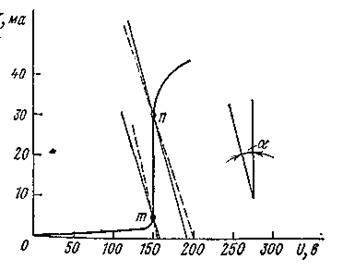
Рисунок 5.22

Решение. Воспользуемся методом эквивалентного генератора. Разомкнем ветвь стабиловольта и найдем напряжение холостого хода:

Определим входное сопротивление линейной части схемы (рис. 5.21) по отношению к зажимам а b:

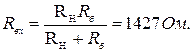
На рис. 5.22 проведем две прямые (сплошные) линии через точки m и n ВАХ стабиловольта так, чтобы тангенс угла (образованного ими с вертикалью) Умноженный на m_U / m_I равнялся R_BX = 1427 ом.

Отрезки, отсекаемые этими прямыми на оси абсцисс, равны U_x _{х .}Из рисунка находим 0,713U_min = 157B, или U_lmin = 220B. Аналогично, 0,713U_max = 192B, или U_lmax = 269B. Следовательно, напряжение U ₁ может изменяться от 220 до 269 в.

Пример 23. На рис. 5.21 при R _б = 2кОм, характеристике стабиловольта рис. 5.22 и U ₁ = 250В определить, в каких пределах можно изменять сопротивление нагрузки R_H, чтобы стабилизатор мог выполнять свои функции по стабилизации выходного напряжения.

Решение. Воспользовавшись методом эквивалентного генератора, определим

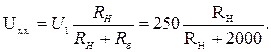
Находим

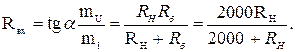
Задача сводится к определению значений R_H, при которых прямые, характеризующие R_BX, будут проходить через точки m и n ВАХ стабиловольта. В данном примере неизвестны ни тангенсы углов α, ни исходные точки на оси абсцисс, из которых должны быть проведены прямые, поэтому решаем задачу путем пробных построений. С этой целью задаемся значениями R_H, подсчитываем соответствующие им U_x _. _x и R _вх.

R кOм	3	4	5	6	7	8
U_х._х, B R_BX, Ом	150 1200	167 1330	178 1425	187 1500	194 1555	200 1600

По данным таблицы проводим несколько лучей. Графически находим, что прямые (см. пунктирные прямые на рис. 5.22) пройдут через точки m и n соответственно при R_н_min = 3,3 кОм и R_H _max = 8 кОм.

Рисунок 5.23

Рисунок 5.24

Входное (усиливаемое) напряжение подается на сетку лампы. На выходе усилителя (зажимы а и b) включена нагрузка R_H.

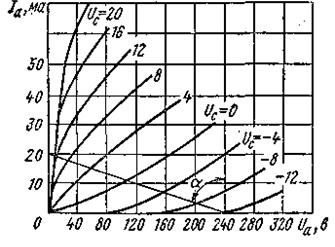
Сетка триода расположена ближе к катоду, чем анод. Влияние поля сетки на поток электронов с катода на анод значительно больше влияния поля анода. Поэтому сравнительно незначительные изменения напряжения на сетке приводят к резкому изменению анодного тока и напряжения на выходе усилителя. Для анодной цепи Е = U_a + I_aR_H. Зависимость напряжения выхода (I_HR_H = Е – U_H) от напряжения входа (U_C) строится с помощью семейства кривых рис. 5.23.

Пример 25. Построить зависимость U _вых = f ( U_c ) для схемы рис. 5.24, если R_Н = 12 кОм и Е = 240 В. Триод 6С2С.

Решение. Из точки I_а = 0, U_а = Е под углом α к вертикали (tg α m_U / m_I = 12 000) проводим прямую. Точки пересечения ее с анодными характеристиками дают соответствующие значения I _а и U_C. Зависимость U _вых = f ( U_c ) отличается от зависимости I _а = f ( U_c ) (рис. 5.25) только масштабом (U _Н = I _Н R _Н , R _Н = const).

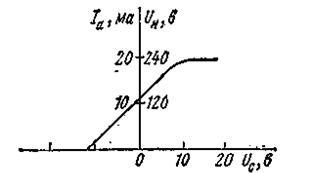
Рисунок 5.25

Глава 5

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

ПОСТОЯННОГО ТОКА

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Дата: 2018-11-18, просмотров: 436.

12 3 4 5 6 Следующая ⇒