Схема параллельного соединения двух НС изображена на рис. 5.4а; ВАХ ее на рис 5.4б. При построении результирующей ВАХисходят из того, что напряжения на НС1 и НС2 равны в силу их параллельного соединения, а ток I в неразветвленной части схемы равен сумме токов I ₁ и I ₂:

I = I ₁ + I _5.

Кривая 3 рис. 5.4б представляет собой ВАХ параллельного соединения. Строим ее следующим образом. Задаемся произвольно напряжением U, например, равным отрезку О m. Проводим через точку т вертикаль. Складываем отрезок mn, равный току в НС2, с отрезком mp, равным току в НС1:

.

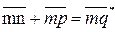Отрезок mq равен току в неразветвленной части цепи при напряжении О m. Аналогично определяют и другие точки результирующей ВАХ параллельного соединения.

Рисунок 5.4

          5.6. ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ НЕЛИНЕЙНЫХ СОПРОТИВЛЕНИЙ

На рис. 5.5 изображена схема последовательного соединения НСЗ и двух параллельно соединенных НС1 и НС5. Требуется найти токи в ветвях схемы.

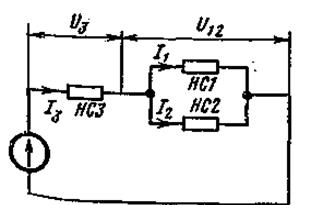
Рисунок. 5.5

     Заданы ВАХ нелинейных сопротивлений (кривые 1, 2, 3, рис. 5.6) и э. д. с. Е. Сначала строим ВАХ параллельного соединения в соответствии с п. 5.5 (кривая 1 + 2 на рис. 5.6). После этого цепь сводится к последовательному соединению НСЗ и НС, имеющего ВАХ 1 + 5.

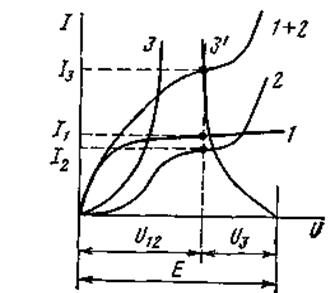
Рисунок 5.6

Применяем второй способ построения, описанный в п. 5.5. Кривая 3^/ рис. 5.6 представляет собой ВАХ НСЗ, зеркально отраженную _fотносительно вертикали, проведенной через точку U = Е. В точкепересечения кривой 3' с кривой 1+2 удовлетворяется второй закон Кирхгофа U ₃ + U ₁₂ = Е. Сумма токов I ₁ и I ₂ равна току I ₃.

РАСЧЕТ РАЗВЕТВЛЕННОЙ НЕЛИНЕЙНОЙ ЦЕПИ МЕТОДОМ

 ДВУХ УЗЛОВ

     Для схем, содержащих только два узла или приводящихся к ним, широко применяют метод двух узлов. Рассмотрим его на примере схемы рис. 5.7. В схеме три НС и три э. д. с. Пусть ВАХ НС изображаются кривыми рис. 5.8а, б и в. Для определенности положим, что Е₁ > Е₂> Е₃. Выберем положительные направления для токов. Пусть, например, все токи на­правлены к узлу а. Тогда по первому закону Кирхгофа

I ₁ + I ₂ + I ₃ = 0.                                               (5.1)

Рисунок 5.7

Каждый из токов является нелинейной функцией падения напряжения на своем НС. Так, I ₁ является функцией U ₁, I ₂ - функцией _U2 и I ₃ - функцией U ₃.

Выразим все токи в функции не от различных переменных (U_lt U₂, U₃), а в функции одного переменного - напряжения U_ab между двумя узлами:

U₁ = E₁ - U_ab;                                                         (5.2)

U₂ = E₂ - U_ab;                                                        (5.3)

U ₃ = E ₃ - U_ab.                                                         (5.4)

Таким образом, возникает задача о перестройке кривой I ₁ = f ( U ₁ ) в кривую I ₁ = f ( U_ab ), кривой I ₂ = f ( U ₂ ) - в кривую I ₂ = f ( U_ab ) и т. д. На рис. 5.9 показано, как из кривой I ₁ = f ( U ₁ ) (рис. 5.8а) получить кривую I ₁ = f ( U_ab ) - точки соответственно обозначены одинаковыми цифрами.

Для точки 5 кривой рис. 5.8а I ₁ = 0 и U ₁ = 0; при этом U_ab = Е₁ (формула (5.2)], т. е. начало кривой I ₁ = f ( U_ab ) сдвинуто в точку U_ab = Е₁.

Росту U ₁ при U ₁  > 0 соответствует убыль U_ab. Для точки 2 при значении U = Е_г напряжение U _аЬ = 0. Росту U ₁ при U ₁ < 0 отвечает рост U_atb причем U_ab > Е₁.

На основании изложенного рекомендуется поступать следующим образом:

  1) сместить кривую I ₁ = f ( U ₁ ) параллельно самой себе так, чтобы ее начало находилось в точке U_ab = Е₁. Кривая, полученная в результате переноса. представлена пунктиром на рис. 5.9;

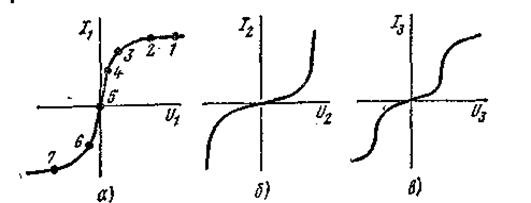
Рисунок 5.8

2) провести через точку U_ab = Е₁ вертикаль и зеркально отразить пунктирную кривую относительно вертикали.

Аналогичным образом производится перестройка кривых и для других ветвей схемы. Нанесем кривые I ₁ = f ( U_ab ), I ₂ = f ( U_ab ) и I ₃ = f ( U_ab ) на одном ри-сунке (на рис. 5.10 кривые 1, 2, 3) а построим кривую I ₁ + I ₂ + I ₃ = f ( U_ab ) (на рис. 5.10 кривая 4), просуммировав ординаты кривых 1, 2, 3.

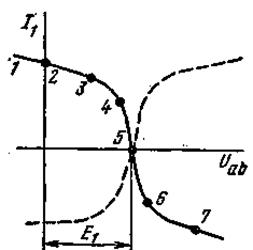
Рисунок 5.9

Точка m пересечения кривой 4 с осью абсцисс дает значение U_ab, при котором удовлетворяется уравнение (5.1). Восставим в этой точке перпендикуляр к оси абсцисс. Ординаты точек пересечения перпендикуляра с кривыми 1, 2, 3 дадут соответственно токи I _1, I ₂ и I ₃ по величине и по знаку.

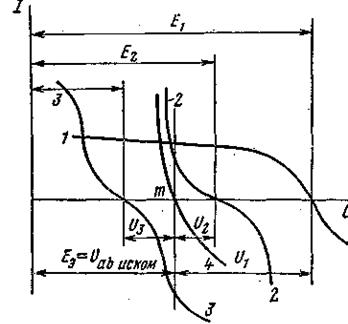
Рисунок 5.10