Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1.	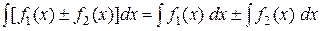;	10.	;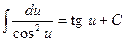
2.	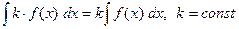;	11.	;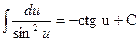
3.	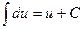;	12.	;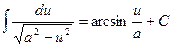
4.	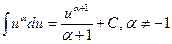;	13.	;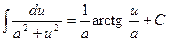
5.	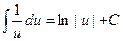, 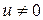;	14.	;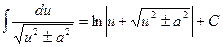
6.	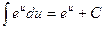;	15.	;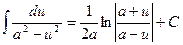
7.	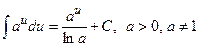;	16.	;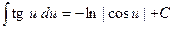
8.	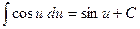;	17.	;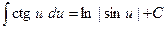
9.	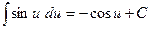;	18.	;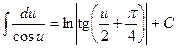
		19.	.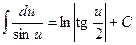

 

В формулах 3 – 19 переменная u может быть как независимой переменной, так и некоторой функцией аргумента x .

НЕПОСРЕДСТВЕННОЕ  ИНТЕГРИРОВАНИЕ

Пример 1. Найти интеграл 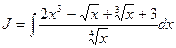 (см. М-1540, стр. 12–13).

Решение. Преобразуем подынтегральное выражение и воспользуемся формулами 1, 2, 4. Получим

.

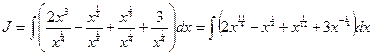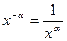Здесь мы применили известные формулы  и . Следовательно,

.

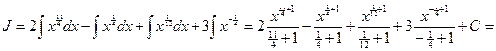
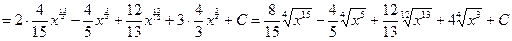Проверим найденный результат дифференцированием. Найдем

,

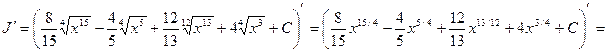
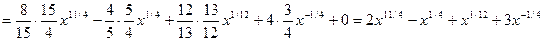что совпадает с подынтегральным выражением, и, следовательно, интегрирование проведено правильно.

 

 

МЕТОД ПОДСТАНОВКИ ИЛИ ЗАМЕНЫ ПЕРЕМЕННОЙ

Пример 2. Вычислить интеграл 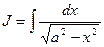 (см. М-1540, стр. 14).

Решение. Сделаем подстановку 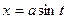, тогда  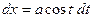и 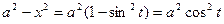. Поэтому интеграл преобразуется к виду

.

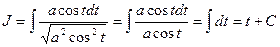Из подстановки 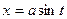 найдем  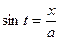и 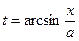. Тогда .

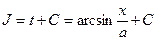Таким образом, мы получили табличный интеграл

.

 

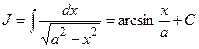Пример 3. Вычислить интеграл 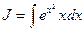 (см. М-1540, стр. 14).

Решение. Сделаем подстановку 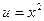. Тогда 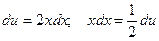. Переходя под интегралом к переменной 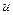, получим

.

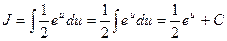Возвращаясь к переменной 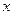, найдем окончательно .

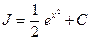Сделаем проверку 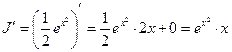, что совпадает с подынтегральным выражением.

Аналогичным образом вычислим еще несколько интегралов, не делая подробных объяснений.

 

Пример 4.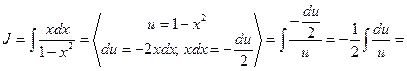

 

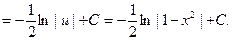
Пример 5. .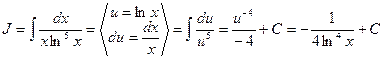

Пример 6. .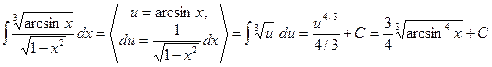

 

 

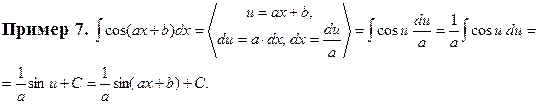
Пример 8.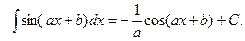

 

МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ

Пример 9. Вычислить интеграл 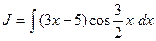 (см. М-1540, стр. 15).

Решение. Обозначим 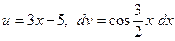. Тогд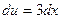а , а 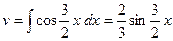 (см. пример 7, формулу (3) ) Получим

 

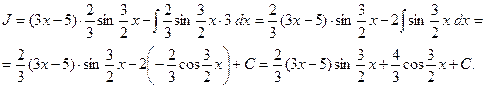
Пример 10. Вычислить интеграл 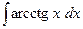 (см. М-1540, стр. 15).

Решение.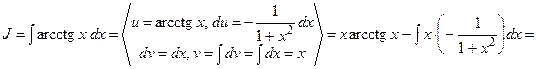

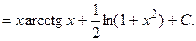 (см. пример 4).

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ

Пример 11. Вычислить интеграл 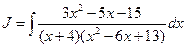 (см. М-1540, стр. 16–18).

Решение. Представим подынтегральную дробь в виде суммы простейших дробей. Так как квадратный трехчлен 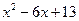 имеет отрицательный дискриминант 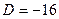, то

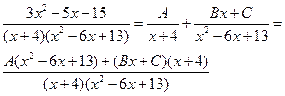
Отсюда получаем

  ,

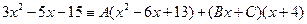или ,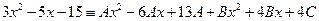

или .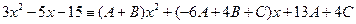

Приравнивая коэффициенты при одинаковых степенях 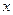 в левой и правой частях, получим:

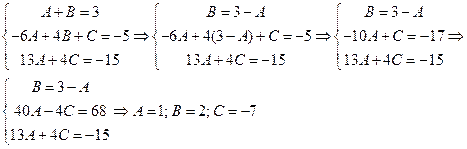
Таким образом,

.

 

 

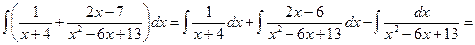
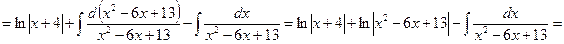
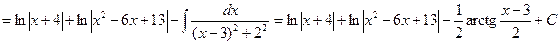ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ

Пример 12. Вычислить интеграл 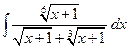 (см. М-1540, стр. 18–19).

Решение. Так как 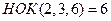, сделаем подстановку 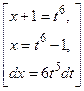. Тогда  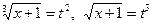и .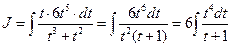

Разделив 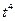 на 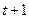, получим

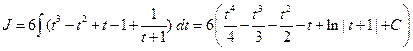, где .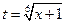

Следовательно,

 

 

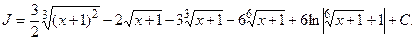
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Пример 13. Вычислить интеграл 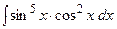(см. М-1540, стр. 19).

Решение.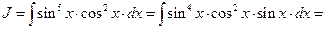

 

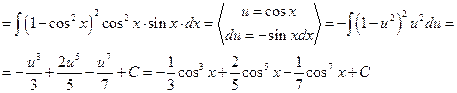
Пример 14. Вычислить интеграл 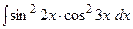 (см. М-1540, стр. 19).

Решение.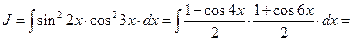

.

 

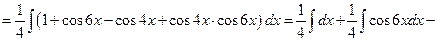
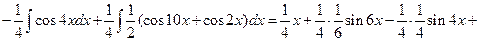
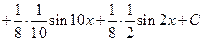Пример 15. Вычислить интеграл 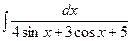(см. М-1540, стр. 19).

Решение. Применим универсальную подстановку

 

 

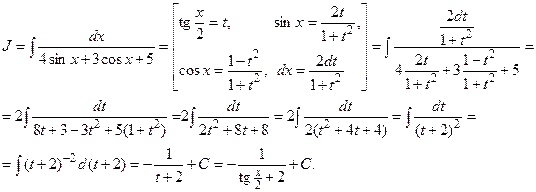
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Пример 16. Вычислить определенный интеграл

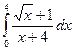(см. М-1540, стр. 20–21).

Решение.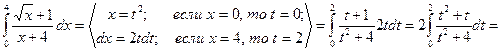

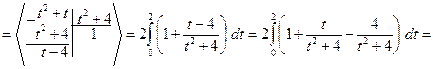
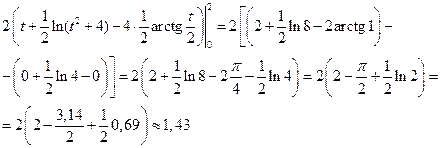
При вычислении этого интеграла были применены формулы

 

 

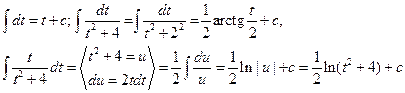
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Несобственные интегралы по бесконечному промежутку

Пример 17. Вычислить несобственный интеграл 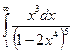 или доказать его расходимость (см. М-1540, стр. 23).

Решение.

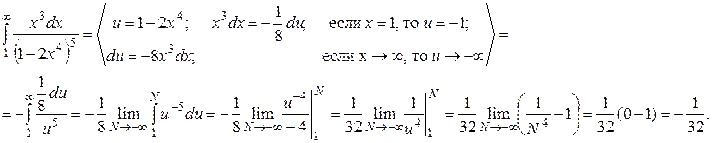
Таким образом, несобственный интеграл равен 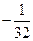, т. е. он сходится.