ВЫСШАЯ МАТЕМАТИКА
Контрольные задания и примеры их решения для студентов
2 курса инженерно-технических специальностей
заочной формы обучения
Часть 3

Составители: Е. Н. Бесперстова
В. А.Гордеев
О. Ф. Маркович
Самара
| |
УДК 517
Высшая математика : контрольные задания и примеры их решения для студентов 2 курса инженерно-технических специальностей заочной формы обучения / составители : Е. Н. Бесперстова, В. А. Гордеев, О. Ф. Маркович. – Самара : СамГУПС, 2009. – 34 с.
Утверждены на заседании кафедры 02.03.09, протокол № 5.
Печатаются по решению редакционно-издательского совета университета.
Контрольные задания составлены в соответствии с Государственным образовательным стандартом и типовой программой по высшей математике и охватывают следующие разделы: неопределенный и определенный интегралы, дифференциальные уравнения, кратные и криволинейные интегралы.
Предназначены для студентов заочной формы обучения инженерно-технических специальностей.
Составители: ст.преп. Елена Николаевна Бесперстова
ст. преп. Владимир Александрович Гордеев
доц. Олег Филиппович Маркович
Рецензенты: к.т.н., доцент СГУ Г. В. Воскресенская;
к.т.н., доцент СамГУПС Ю. В. Гуменникова
Под редакцией к.т.н., доц. В. П. Кузнецова
Подписано в печать 08.12.2009. Формат 60×90 1/16.
Усл. печ. л. 2,1. Заказ № 230.
| |
Порядок выполнения и защиты контрольных работ
По высшей математике
1. По курсу высшей математики 3 семестра, предусмотрено выполнение двух контрольных работ. В каждом из заданий задачи разбиты на 30 вариантов. Номер варианта контрольных работ определяется остатком от деления на 30 числа, образованного последними двумя цифрами учебного шифра, указанного в зачетной книжке студента. Если последние две цифры образуют число, меньшее 30, то они и определяют номер варианта.
2. Каждая из контрольных работ выполняется в тетради. На лицевой стороне обложки тетради указать название учебного заведения, номер контрольной работы по высшей математике, Ф.И.О. студента, номер учебного шифра, Ф.И.О. преподавателя, рецензирующего работу.
3. Решение каждой из задач оформить с записью номера задания, номера задачи варианта, условия задачи. Решение задачи выполнить со всеми развернутыми расчетами и краткими пояснениями, необходимые рисунки по ходу решения задач выполнять в карандашном исполнении и использованием чертежных инструментов.
4. В конце каждой контрольной работы привести список используемой литературы, поставить подпись и дату представления работы.
5. Прорецензированная работа с отметкой «допущена к собеседованию» защищается студентом до начала экзаменационной сессии.
6. Студенты, не защитившие контрольных работ по математике, к сдаче экзамена не допускаются.
7. Контрольные работы с отметкой рецензента «работа не допущена к собеседованию» переделываются студентом заново с учетом замечаний рецензента и направляются на повторную проверку.
Рабочая программа, теоретические сведения и методические указания для выполнения контрольных заданий указаны в методических указаниях №1540 (сокращенно М-1540).
Рекомендуемая литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. – Т.1. – М.: Интеграл-пресс, 2002.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – Т.1. –М.: Дрофа, 2007.
3. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения, кратные интегралы. Ряды. Функции комплексного переменного. – Т.3. – М.: Дрофа, 2005.
4. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – Т. 1,2. – М.: Высшая школа,2002 .
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 2001.
6. Бесперстова Е.Н., Додонова Н.Л., Маркович О.Ф., Фролов В.А. Методические указания, рабочая программа и контрольные задания для студентов заочной формы обучения инженерно-технических специальностей. Часть 3. Самара: СамГАПС, 2005.
Контрольная работа № 5
1. Найдите неопределенные интегралы.
1.1. a) 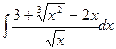 ;
b) ;
b) 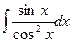 ;
c) ;
c) 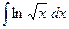 ;
d) ;
d) 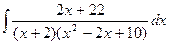 ;
e) ;
e) 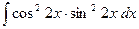 . .
| 1.2. a) 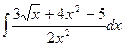 ;
b) ;
b) 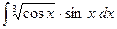 ;
c) ;
c) 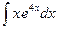 ;
d) ;
d) 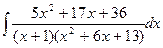 ;
e) ;
e) 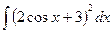 . .
|
1.3. a) 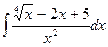 ;
b) ;
b) 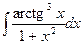 ;
c) ;
c) 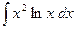 ;
d) ;
d) 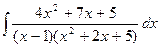 ;
e) ;
e) 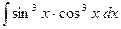 . .
| 1.4. a) 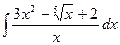 ;
b) ;
b) 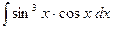 ;
c) ;
c) 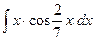 ;
d) ;
d) 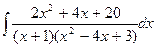 ;
e) ;
e) 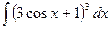 . .
|
1.5. a) 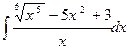 ;
b) ;
b) 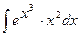 ;
c) ;
c) 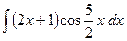 ;
d) ;
d) 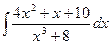 ;
e) ;
e) 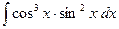 . .
| 1.6. a) 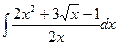 ;
b) ;
b) 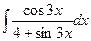 ;
c) ;
c) 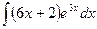 ;
d) ;
d) 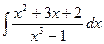 ;
e) ;
e) 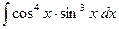 . .
|
1.7. a) 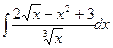 ;
b) ;
b) 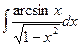 ;
c) ;
c) 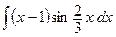 ;
d) ;
d) 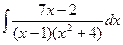 ;
e) ;
e) 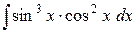 . .
| 1.8. a) 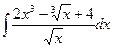 ;
b) ;
b) 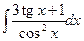 ;
c) ;
c) 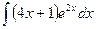 ;
d) ;
d) 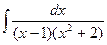 ;
e) ;
e) 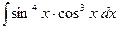 . .
|
1.9. a) 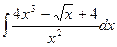 ;
b) ;
b) 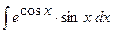 ;
c) ;
c) 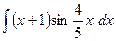 ;
d) ;
d) 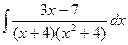 ;
e) ;
e) 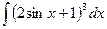 . .
| 1.10. a) 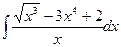 ;
b) ;
b) 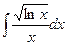 ;
c) ;
c) 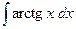 ;
d) ;
d) 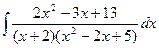 ;
e) ;
e) 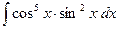 . .
|
1.11. a) 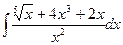 ;
b) ;
b) 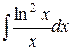 ;
c) ;
c) 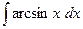 ;
d) ;
d) 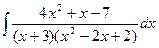 ;
e) ;
e) 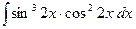 . .
| 1.12. a) 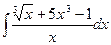 ;
b) ;
b) 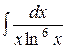 ;
c) ;
c) 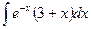 ;
d) ;
d) 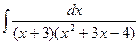 ;
e) ;
e) 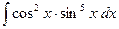 . .
|
1.13. a) 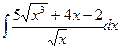 ;
b) ;
b) 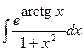 ;
c) ;
c)  ;
d) ;
d) 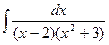 ;
e) ;
e) 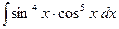 . .
| 1.14. a) 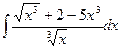 ;
b) ;
b) 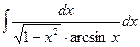 ;
c) ;
c) 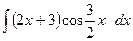 ;
d) ;
d) 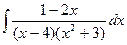 e)
e) 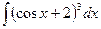 . .
|
1.15. a) 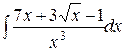 ;
b) ;
b) 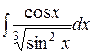 ;
c) ;
c) 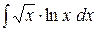 ;
d) ;
d) 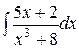 ;
e) ;
e) 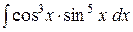 . .
| 1.16. a) 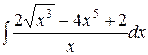 ;
b) ;
b) 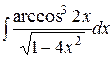 ;
c) ;
c) 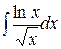 ;
d) ;
d) 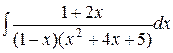 ;
e) ;
e) 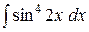 . .
|
1.17. a) 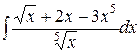 ;
b) ;
b) 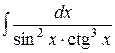 ;
c) ;
c) 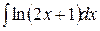 ;
d) ;
d) 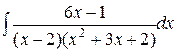 ;
e) ;
e) 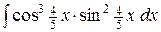 . .
| 1.18. a) 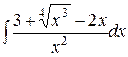 ;
b) ;
b) 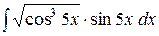 ;
c) ;
c) 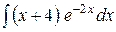 ;
d) ;
d) 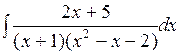 ;
e) ;
e) 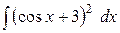 . .
|
1.19. a) 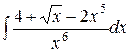 ;
b) ;
b) 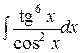 ;
c) ;
c) 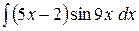 ;
d) ;
d) 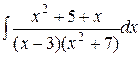 ;
e) ;
e) 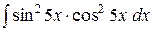 . .
| 1.20. a) 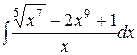 ;
b) ;
b) 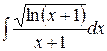 ;
c) ;
c) 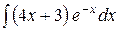 ;
d) ;
d) 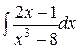 ;
e) ;
e) 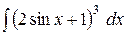 . .
|
1.21. a) 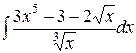 ;
b) ;
b)  ;
c) ;
c)  ;
d) ;
d) 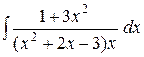 ;
e) ;
e) 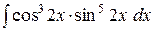 . .
| 1.22. a) 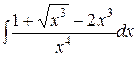 ;
b) ;
b) 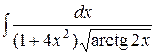 ;
c) ;
c) 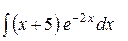 ;
d) ;
d) 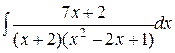 ;
e) ;
e) 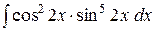 . .
|
1.23. a) 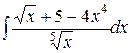 ;
b) ;
b) 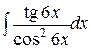 ;
c) ;
c) 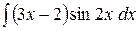 ;
d) ;
d) 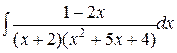 ;
e) ;
e) 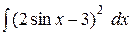 . .
| 1.24. a) 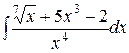 ;
b) ;
b) 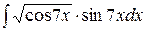 ;
c) ;
c) 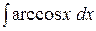 ;
d) ;
d) 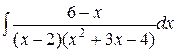 ;
e) ;
e) 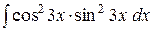 . .
|
1.25. a) 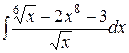 ;
b) ;
b) 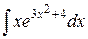 ;
c) ;
c) 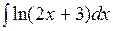 ;
d) ;
d) 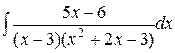 ;
e) ;
e) 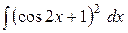 . .
| 1.26. a) 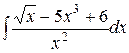 ;
b) ;
b) 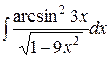 ;
c) ;
c) 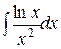 ;
d) ;
d) 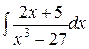 ;
e) ;
e) 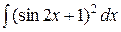 . .
|
1.27. a) 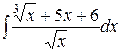 ;
b) ;
b) 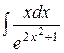 ;
c) ;
c) 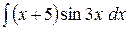 ;
d) ;
d) 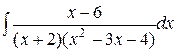 ;
e) ;
e) 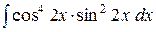 . .
| 1.28. a) 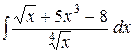 ;
b) ;
b) 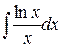 ;
c) ;
c) 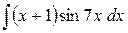 ;
d) ;
d) 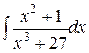 ;
e) ;
e) 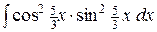 . .
|
1.29. a) 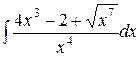 ;
b) ;
b) 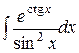 ;
c) ;
c)  ;
d) ;
d) 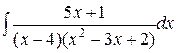 ;
e) ;
e) 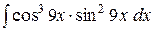 . .
| 1.30. a) 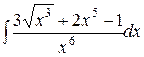 ;
b) ;
b) 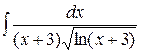 ;
c) ;
c) 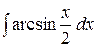 ;
d) ;
d) 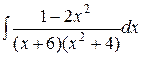 ;
e) ;
e) 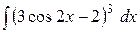 . .
|
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
2 . 1 . 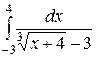 ; ;
| 2.2. 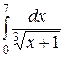 ; ;
| 2.3. 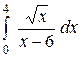 ; ;
|
2.4. 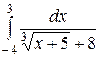 ; ;
| 2. 5. 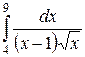 ; ;
| 2.6. 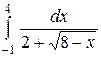 ; ;
|
2.7. 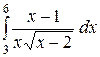 ; ;
| 2.8 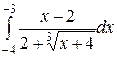 ; ;
| 2. 9 . 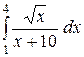 ; ;
|
2.10. 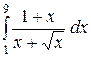 ; ;
| 2.11. 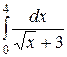 ; ;
| 2.12. 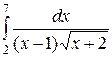 ; ;
|
2. 13 . 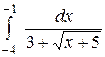 ; ;
| 2.14. 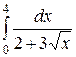 ; ;
| 2.15. 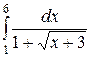 ; ;
|
2.16. 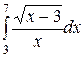
| 2.17 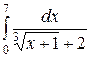 ; ;
| 2.18. 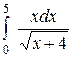 ; ;
|
2.19. 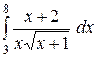 ; ;
| 2.20. 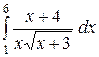 ; ;
| 2.21 . 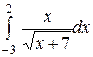 ; ;
|
2.22. 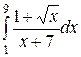 ; ;
| 2.23. 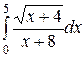 ; ;
| 2.24. 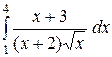 ; ;
|
2 . 25. 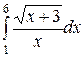 ; ;
| 2.26. 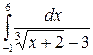 ; ;
| 2.27. 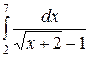 ; ;
|
2.28. 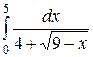
| 2.29. 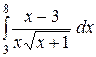 ; ;
| 2.30. 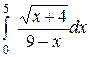 . .
|
3. Вычислите несобственные интегралы или докажите их расходимость.
3.1. 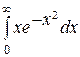
| 3.2. 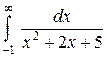
| 3.3. 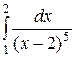
|
3.4. 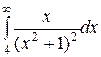
| 3.5. 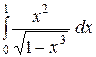
| 3.6. 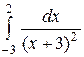
|
3.7. 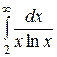
| 3.8. 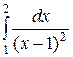
| 3.9. 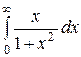
|
3.10. 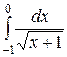
| 3.11 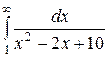
| 3.12. 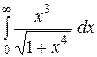
|
3.13. 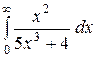
| 3.14. 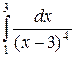
| 3.15. 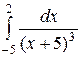
|
3.16. 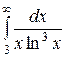 . .
| 3.17. 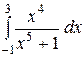
| 3.18. 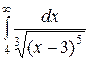
|
3.19. 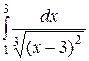
| 3.20. 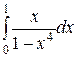 . .
| 3.21. 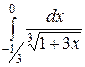
|
3.22. 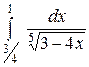
| 3.23. 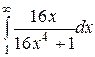
| 3.24. 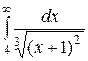 . .
|
3.25. 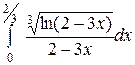
| 3.26. 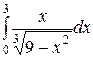
| 3.27. 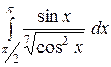
|
3.28. 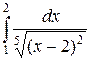 . .
| 3.29. 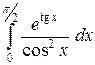 . .
| 3.30 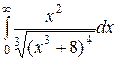
|
4. Произвести вычисления.
4.1. Вычислите площадь фигуры, ограниченной параболой 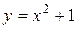 и прямой
и прямой 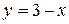 .
.
4.2. Вычислите длину дуги кривой 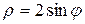 .
.
4.3. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми 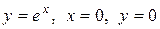 ,x=1.
,x=1.
4.4. Вычислите площадь фигуры, ограниченной линией 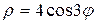 .
.
4.5. Вычислите длину дуги арки циклоиды 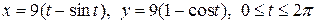 .
.
4.6. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболой 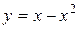 и прямой
и прямой 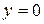 .
.
4.7. Вычислите длину дуги кривой 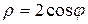 .
.
4.8. Вычислите площадь фигуры, ограниченной линиями 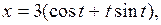
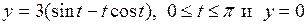 .
.
4.9. Вычислите длину дуги полукубической параболы 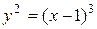 от точки
от точки 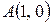 до точки
до точки 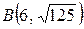 .
.
4.10. Вычислите площадь фигуры, ограниченной линией 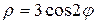 .
.
4.11. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линией 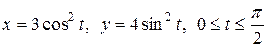 .
.
4.12. Вычислите длину дуги полукубической параболы 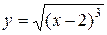 от точки
от точки 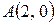 до точки
до точки 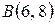 .
.
4.13. Вычислите площадь фигуры, ограниченной кардиоидой 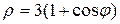 .
.
4.14. Вычислите площадь фигуры, ограниченной линиями 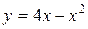 и
и 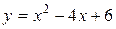 .
.
4.15. Вычислите площадь фигуры, ограниченной одной аркой циклоиды 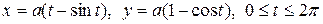 и осью Ох.
и осью Ох.
4.16. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми 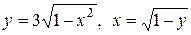 и осью Оу
и осью Оу  .
.
4.17. Вычислите длину дуги кардиоиды 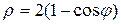 .
.
4.18. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболами 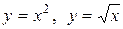 .
.
4.19. Вычислите площадь фигуры, ограниченной параболой 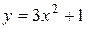 и прямой
и прямой 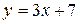 .
.
4.20. Вычислите длину астроиды 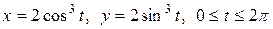 .
.
4.21. Вычислите площадь фигуры, ограниченной четырехлепестковой розой 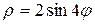 .
.
4.22. Вычислите длину дуги кривой 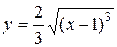 , ограниченной прямыми
, ограниченной прямыми 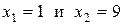 .
.
4.23. Вычислите площадь фигуры, ограниченной линиями 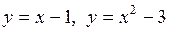 .
.
4.24. Вычислите объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной кривыми 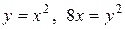 .
.
4.25. Вычислите площадь фигуры, ограниченной линией 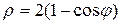 .
.
4.26. Вычислите длину дуги кривой 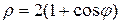 .
.
4.27. Вычислите длину дуги данной линии 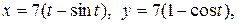
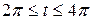 .
.
4.28. Вычислите объем тела, полученного вращением вокруг оси Оу линии 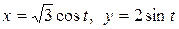 .
.
4.29. Вычислите площадь фигуры, ограниченной астроидой 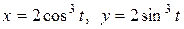 .
.
4.30. Вычислите площадь фигуры, ограниченной линиями 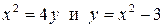 .
.
5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
| 5.1. | 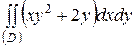 ; ;
| 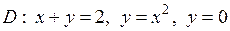 . .
|
| 5.2. | 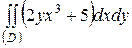 ; ;
| 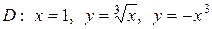 . .
|
| 5.3. | 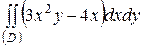 ; ;
| 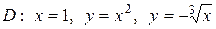 . .
|
| 5.4. | 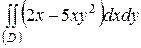 ; ;
| 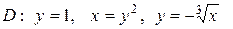 . .
|
| 5.5. | 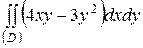 ; ;
| 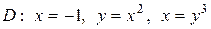 . .
|
| 5.6. | 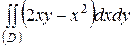 ; ;
| 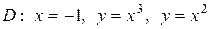 . .
|
| 5.7. | 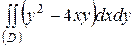 ; ;
| 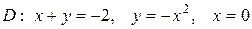 . .
|
| 5.8. | 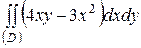 ; ;
| 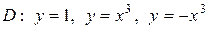 . .
|
| 5.9. | 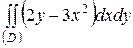 ; ;
| 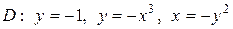 . .
|
| 5.10. | 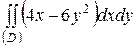 ; ;
| 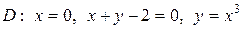 . .
|
| 5.11 | 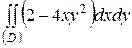 ; ;
| 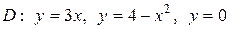 . .
|
| 5.12. | 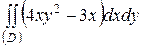 ; ;
| 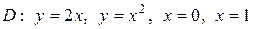 . .
|
| 5.13. | 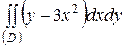 ; ;
| 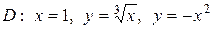 . .
|
| 5.14. | 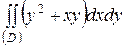 ; ;
| 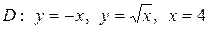 . .
|
| 5.15. | 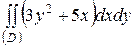 ; ;
| 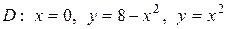 . .
|
| 5.16. | 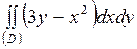 ; ;
| 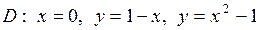 . .
|
| 5.17. | 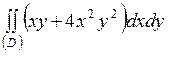 ; ;
| 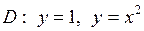 . .
|
| 5.18. | 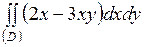 ; ;
| 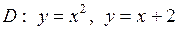 . .
|
| 5.19. | 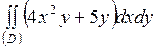 ; ;
| 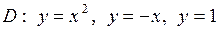 . .
|
| 5.20. | 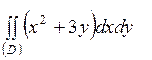 ; ;
| 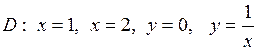 . .
|
| 5.21. | 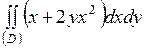 ; ;
| 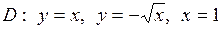 . .
|
| 5.22. | 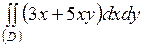 ; ;
| 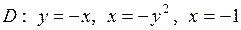 . .
|
| 5.23. | 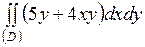 ; ;
| 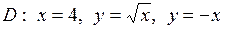 . .
|
| 5.24. | 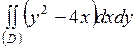 ; ;
| 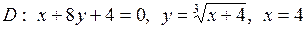 . .
|
| 5.25. | 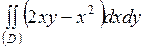 ; ;
| 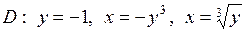 . .
|
| 5.26. | 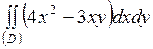 ; ;
| 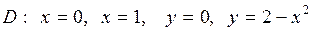 . .
|
| 5.27. | 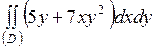 ; ;
| 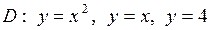 . .
|
| 5.28. | 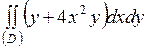 ; ;
| 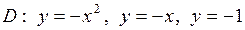 . .
|
| 5.29. | 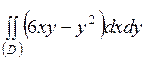 ; ;
| 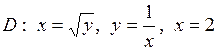 . .
|
| 5.30. | 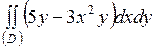 ; ;
| 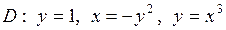 . .
|
6. Вычислите криволинейный интеграл
6.1. 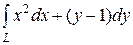 , где L — путь, соединяющий точки О(0, 0) и А(1, 1)
, где L — путь, соединяющий точки О(0, 0) и А(1, 1)
a) по кривой 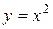 ; b) по ломаной линии ОВА, где В(0, 1);
; b) по ломаной линии ОВА, где В(0, 1);
c) по окружности 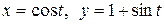 .
.
6.2. 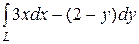 , где L — путь, соединяющий точки А(1, 0) и В(0, 1)
, где L — путь, соединяющий точки А(1, 0) и В(0, 1)
a) по прямой 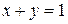 ; b) по ломаной линии АСВ, где С(1, 1);
; b) по ломаной линии АСВ, где С(1, 1);
c) по окружности 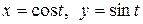 .
.
6.3. 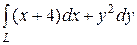 , где L — путь, соединяющий точки О(0, 0) и А(–4, 2)
, где L — путь, соединяющий точки О(0, 0) и А(–4, 2)
a) по прямой 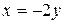 ; b) по ломаной линии О C А, где C(0, 2);
; b) по ломаной линии О C А, где C(0, 2);
c) по эллипсу 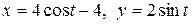 .
.
6.4. 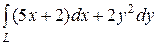 , где L — путь, соединяющий точки А(–2, 0) и В(0, 2)
, где L — путь, соединяющий точки А(–2, 0) и В(0, 2)
a) по прямой 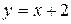 ; b) по ломаной линии АСВ, где С(–2, 2);
; b) по ломаной линии АСВ, где С(–2, 2);
c) по окружности 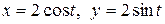 .
.
6.5. 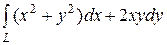 , где L — путь, соединяющий точки А(0, –3) и В(3, 0)
, где L — путь, соединяющий точки А(0, –3) и В(3, 0)
a) по прямой 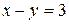 ; b) по ломаной линии АСВ, где С(3, –3);
; b) по ломаной линии АСВ, где С(3, –3);
c) по параболе 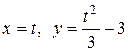 .
.
6.6. 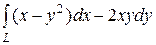 , где L — путь, соединяющий точки А(–1, 0) и В(0, –1)
, где L — путь, соединяющий точки А(–1, 0) и В(0, –1)
a) по прямой 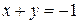 ; b) по ломаной линии АСВ, где С(–1,–1);
; b) по ломаной линии АСВ, где С(–1,–1);
c) по параболе 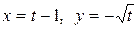 .
.
6.7. 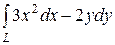 , где L — путь, соединяющий точки А(2, 0) и В(0, 4)
, где L — путь, соединяющий точки А(2, 0) и В(0, 4)
a) по прямой 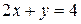 ; b) по ломаной линии АСВ, где С(2, 4);
; b) по ломаной линии АСВ, где С(2, 4);
c) по эллипсу 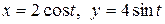 .
.
6.8. 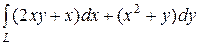 , где L — путь, соединяющий точки А
, где L — путь, соединяющий точки А 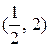 и В
и В 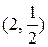
a) по гиперболе 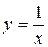 ; b) по ломаной линии АСВ, где С(2, 2);
; b) по ломаной линии АСВ, где С(2, 2);
c) по прямой 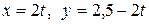 .
.
6.9. 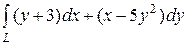 , где L — путь, соединяющий точки А(–1, 0) и В(0, 2)
, где L — путь, соединяющий точки А(–1, 0) и В(0, 2)
a) по прямой 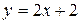 ; b) по ломаной линии АСВ, где С(–1, 2);
; b) по ломаной линии АСВ, где С(–1, 2);
c) по эллипсу 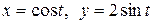 .
.
6.10. 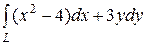 , где L — путь, соединяющий точки А(4, 0) и В(0, 2)
, где L — путь, соединяющий точки А(4, 0) и В(0, 2)
a) по параболе 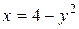 ; b) по ломаной линии АСВ, где С(4, 2);
; b) по ломаной линии АСВ, где С(4, 2);
c) по эллипсу 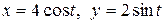 .
.
6.11.  , где L — путь, соединяющий точки А(1, 2) и В(2, 1)
, где L — путь, соединяющий точки А(1, 2) и В(2, 1)
a) по прямой 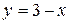 ; b) по ломаной линии АСВ, где С(2, 2);
; b) по ломаной линии АСВ, где С(2, 2);
c) по параболе 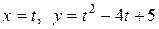 .
.
6.12. 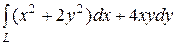 , где L — путь, соединяющий точки А(9, 0) и В(0, 3)
, где L — путь, соединяющий точки А(9, 0) и В(0, 3)
a) по параболе 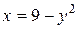 ; b) по ломаной линии АСВ, где С(9, 3);
; b) по ломаной линии АСВ, где С(9, 3);
c) по прямой 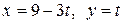 .
.
6.13. 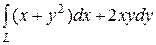 , где L — путь, соединяющий точки А(–1, 0) и В(0, –1)
, где L — путь, соединяющий точки А(–1, 0) и В(0, –1)
a) по прямой 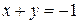 ; b) по ломаной линии АСВ, где С(–1, –1);
; b) по ломаной линии АСВ, где С(–1, –1);
c) по параболе 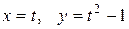 .
.
6.14. 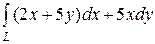 , где L — путь, соединяющий точки А(–1, 0) и В(0, 2)
, где L — путь, соединяющий точки А(–1, 0) и В(0, 2)
a) по прямой 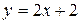 ; b) по ломаной линии АСВ, где С(–1, 2);
; b) по ломаной линии АСВ, где С(–1, 2);
c) по эллипсу 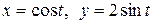 .
.
6.15. 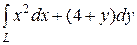 , где L — путь, соединяющий точки А(0, 3) и В(1, 4)
, где L — путь, соединяющий точки А(0, 3) и В(1, 4)
a) по кривой 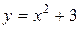 ; b) по ломаной линии АСВ, где С(0, 4);
; b) по ломаной линии АСВ, где С(0, 4);
c) по прямой x = t −3; y = t
6.16. 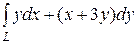 , где L — путь, соединяющий точки А(3,0) и В(0, 3)
, где L — путь, соединяющий точки А(3,0) и В(0, 3)
a) по прямой 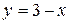 ; b) по ломаной линии АСВ, где С(3, 3);
; b) по ломаной линии АСВ, где С(3, 3);
c) по окружности 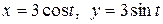 .
.
6.17. 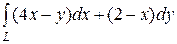 , где L — путь, соединяющий точки А(2, 0) и В(3, 1)
, где L — путь, соединяющий точки А(2, 0) и В(3, 1)
a) по прямой 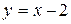 ; b) по ломаной линии АСВ, где С(2, 1);
; b) по ломаной линии АСВ, где С(2, 1);
c) по окружности 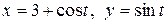 .
.
6.18. 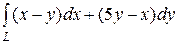 , где L — путь, соединяющий точки А
, где L — путь, соединяющий точки А 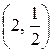 и В
и В 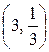
a) по кривой 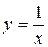 ; b) по ломаной линии АСВ, где С
; b) по ломаной линии АСВ, где С 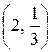 ;
;
c) по прямой 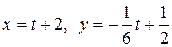 .
.
6.19. 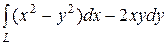 , где L — путь, соединяющий точки А(0, 2) и В(1, 3)
, где L — путь, соединяющий точки А(0, 2) и В(1, 3)
a) по прямой 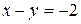 ; b) по ломаной линии АСВ, где С(0, 3);
; b) по ломаной линии АСВ, где С(0, 3);
c) по параболе 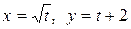 .
.
6.20. 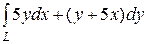 , где L — путь, соединяющий точки А(–4, 0) и В(0, –2)
, где L — путь, соединяющий точки А(–4, 0) и В(0, –2)
a) по параболе 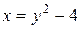 ; b) по ломаной линии АСВ, где С(–4, –2);
; b) по ломаной линии АСВ, где С(–4, –2);
c) по прямой 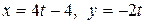 .
.
6.21. 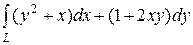 , где L — путь, соединяющий точки А
, где L — путь, соединяющий точки А 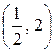 и В
и В 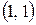
a) по гиперболе 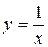 ; b) по ломаной линии АСВ, где С
; b) по ломаной линии АСВ, где С 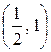 ;
;
c) по прямой 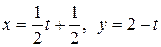 .
.
6.22. 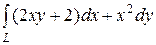 , где L — путь, соединяющий точки O(0, 0) и В(2, 2)
, где L — путь, соединяющий точки O(0, 0) и В(2, 2)
a) по прямой 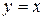 ; b) по ломаной линии O СВ, где С(0, 2);
; b) по ломаной линии O СВ, где С(0, 2);
c) по окружности 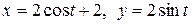 .
.
6.23. 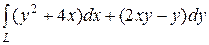 , где L — путь, соединяющий точки О(0, 0) и А
, где L — путь, соединяющий точки О(0, 0) и А 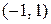
a) по прямой 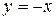 ; b) по ломаной линии ОВА, где В(–1, 0);
; b) по ломаной линии ОВА, где В(–1, 0);
c) по полукубической параболе 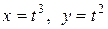 .
.
6.24. 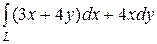 , где L — путь, соединяющий точки А(–2, 5) и В(0, 1)
, где L — путь, соединяющий точки А(–2, 5) и В(0, 1)
a) по прямой 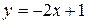 ; b) по ломаной линии АСВ, где С(0, 5);
; b) по ломаной линии АСВ, где С(0, 5);
c) по параболе 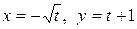 .
.
6.25. 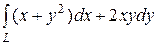 , где L — путь, соединяющий точки А(–1, 0) и В(0, 2)
, где L — путь, соединяющий точки А(–1, 0) и В(0, 2)
a) по прямой 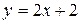 ; b) по ломаной линии АС B, где С(–1, 2);
; b) по ломаной линии АС B, где С(–1, 2);
c) по эллипсу 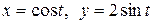 .
.
6.26. 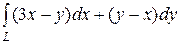 , где L — путь, соединяющий точки А(–2, 0) и В(0, 1)
, где L — путь, соединяющий точки А(–2, 0) и В(0, 1)
a) по прямой 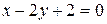 ; b) по ломаной линии АСВ, где С(–2, 1)
; b) по ломаной линии АСВ, где С(–2, 1)
c) по эллипсу 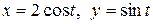 .
.
6.27. 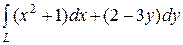 , где L — путь, соединяющий точки А(0, 2) и В(4, 0)
, где L — путь, соединяющий точки А(0, 2) и В(4, 0)
a) по прямой 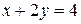 ; b) по ломаной линии АСВ, где С(4, 2);
; b) по ломаной линии АСВ, где С(4, 2);
c) по эллипсу 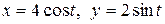 .
.
6.28. 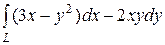 , где L — путь, соединяющий точки А(–1, 0) и В(0, –3)
, где L — путь, соединяющий точки А(–1, 0) и В(0, –3)
a) по прямой 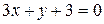 ; b) по ломаной линии АСВ, где С(–1, –3);
; b) по ломаной линии АСВ, где С(–1, –3);
c) по эллипсу 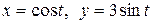 .
.
6.29. 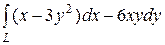 , где L — путь, соединяющий точки А(2, 4) и В(4, 2)
, где L — путь, соединяющий точки А(2, 4) и В(4, 2)
a) по кривой 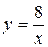 ; b) по ломаной линии АСВ, где С(4, 4);
; b) по ломаной линии АСВ, где С(4, 4);
c) по прямой 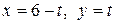 .
.
6.30. 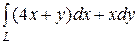 , где L — путь, соединяющий точки А(0, –3) и В(4, 0)
, где L — путь, соединяющий точки А(0, –3) и В(4, 0)
a) по прямой 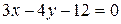 ; b) по ломаной линии АСВ, где С(4, –3);
; b) по ломаной линии АСВ, где С(4, –3);
c) по эллипсу 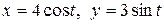 .
.
Примеры решения заданий для выполнения
Контрольной работы № 5
Таблица 1
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример 16. Вычислить определенный интеграл
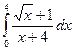 (см. М-1540, стр. 20–21).
(см. М-1540, стр. 20–21).
Решение. 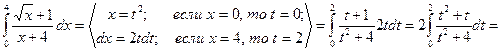
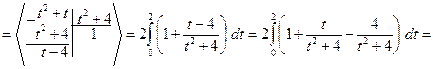
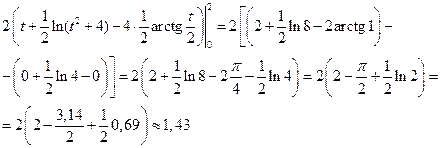
При вычислении этого интеграла были применены формулы
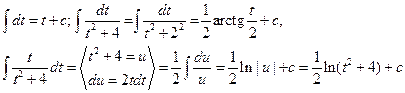
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Решение.
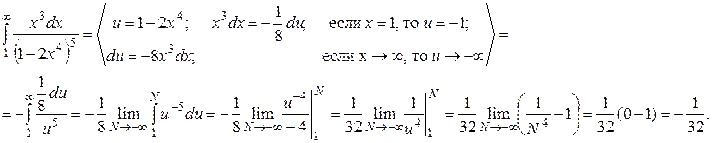
Таким образом, несобственный интеграл равен 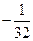 , т. е. он сходится.
, т. е. он сходится.
Решение.
Для построения кривой составим таблицу значений функции.
Таблица 2
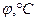
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 |
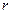
| 3 | 2,55 | 1,5 | 0 | - | - | - | - | - | 0 | 1,5 | 2,55 | 3 |
Для 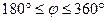 значения
значения 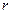 будут повторяться в силу периодичности функции
будут повторяться в силу периодичности функции 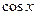 . Строим кривую по точкам (нижняя часть кривой симметрично достраивается) (рис. 3).
. Строим кривую по точкам (нижняя часть кривой симметрично достраивается) (рис. 3).
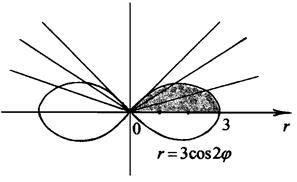
рис. 3
Заметим, что построенная фигура состоит из четырех равных частей, поэтому
| |
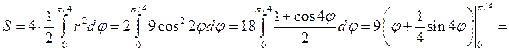
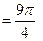 (кв.ед.)
(кв.ед.)
Контрольная работа № 6
Дифференциальные уравнения
7. Найдите общее решение дифференциальных уравнений
| 7 .1. | a) 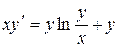 ;
b) ;
b) 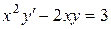 ;
c) ;
c) 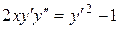 . .
| 7 .2. | a) 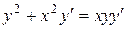 ; ;  b)
b) 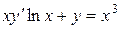 ;
c) ;
c) 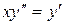 . .
|
| 7 .3. | a) 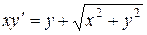 ;
b) ;
b) 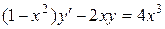 ;
c) ;
c) 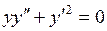 . .
| 7 .4. | a) 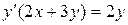 ;
b) ;
b) 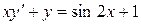 ;
c) ;
c) 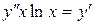 . .
|
| 7 .5. | a) 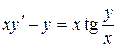 ;
b) ;
b) 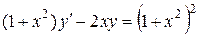 ;
c) ;
c) 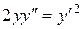 . .
| 7 .6. | a) 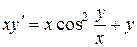 ;
b) ;
b) 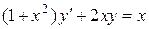 ;
c) ;
c) 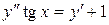 . .
|
| 7 .7. | a) 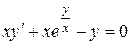 ;
b) ;
b) 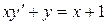 ;
c) ;
c) 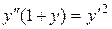 . .
| 7 .8. |
a) 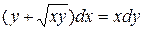 ;
b) ;
b) 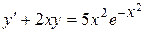 ;
c) ;
c) 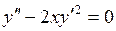 . .
|
| 7 .9. | a) 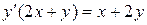 ;
b) ;
b) 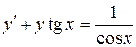 ;
c) ;
c) 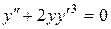 . .
| 7 .10. | a) 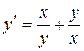 ;
b) ;
b) 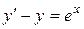 ;
c) ;
c) 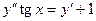 . .
|
| 7 .11. | a) 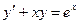 ;
b) ;
b) 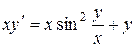 ;
c) ;
c) 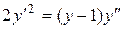 . .
| 7 .12. | a) 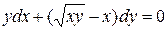 ;
b) ;
b) 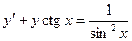 ;
c) ;
c) 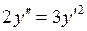 . .
|
| 7 .13. | a) 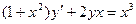 ;
b) ;
b) 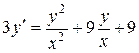 ;
c) ;
c) 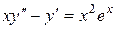 . .
| 7 .14. | a) 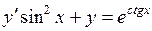 ;
b) ;
b) 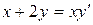 ;
c) ;
c) 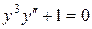
|
| 7 .15. | a) 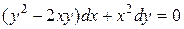 ;
b) ;
b) 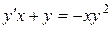 ; ;  c)
c) 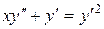 . .
| 7 .16. | a) 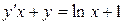 ;
b) ;
b) 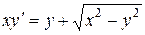 ;
c) ;
c) 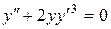 . .
|
| 7 .17. | a) 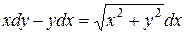 ;
b) ;
b) 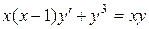 ;
c) ;
c) 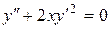 . .
| 7 .18. | a) 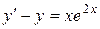 ;
b) ;
b) 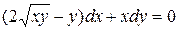 ;
c) ;
c) 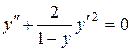 . .
|
| 7 .19. | a) 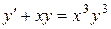 ;
b) ;
b) 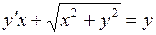 ;
c) ;
c) 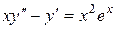 . .
| 7 .20. | a) 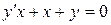 ;
b) ;
b) 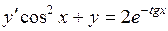 ;
c) ;
c) 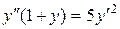 . .
|
| 7 .21. | a) 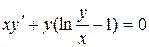 ;
b) ;
b) 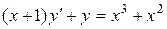 ;
c) ;
c) 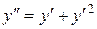 . .
| 7 .22. | a) 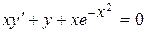 ;
b) ;
b) 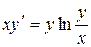 ;
c) ;
c) 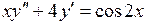 . .
|
| 7 .23. | a) 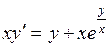 ;
b) ;
b) 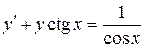 ;
c) ;
c) 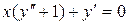 . .
| 7 .24. | a) 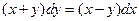 ;
b) ;
b) 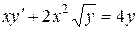 ;
c) ;
c) 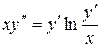 . .
|
| 7 .25. | a) 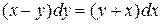 ;
b) ;
b) 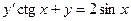 ;
c) ;
c) 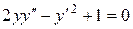 . .
| 7 .26. | a) 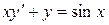 ;
b) ;
b) 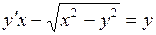 ;
c) ;
c) 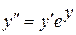 . .
|
| 7 .27. | a) 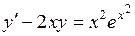 ;
b) ;
b) 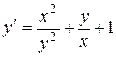 ;
c) ;
c) 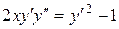 . .
| 7 .28. | a) 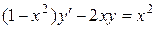 ;
b) ;
b) 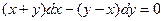 ;
c) ;
c) 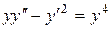 . .
|
| 7 .29. | a) 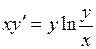 ;
b) ;
b) 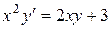 ;
c) ;
c) 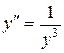 . .
| 7 .30. | a) 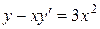 ;
b) ;
b) 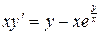 ;
c) ;
c) 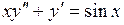 . .
|
8. Найдите общее решение однородных дифференциальных уравнений.
| 8 .1 | a) 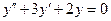 ;
b) ;
b) 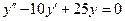 ;
c) ;
c) 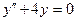 . .
| 8 .2. | a) 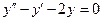 ;
b) ;
b) 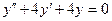 ;
c) ;
c) 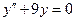 . .
|
| 8 .3. | a) 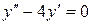 ;
b) ;
b) 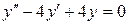 ;
c) ;
c) 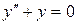 . .
| 8 .4. | a) 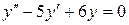 ;
b) ;
b) 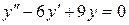 ;
c) ;
c) 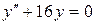 . .
|
| 8 .5. | a) 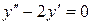 ;
b) ;
b) 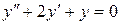 ;
c) ;
c) 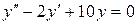 . .
| 8 .6. | a) 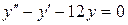 ;
b) ;
b) 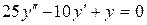 ;
c) ;
c) 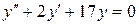 . .
|
| 8 .7. | a) 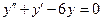 ;
b) ;
b) 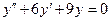 ;
c) ;
c) 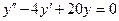 . .
| 8 .8. | a) 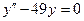 ;
b) ;
b) 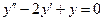 ;
c) ;
c) 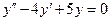 . .
|
| 8 .9. | a) 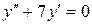 ;
b) ;
b) 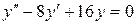 ;
c) ;
c) 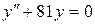 . .
| 8 .10. | a) 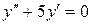 ;
b) ;
b) 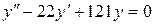 ;
c) ;
c) 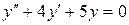 . .
|
| 8 .11. | a) 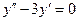 ;
b) ;
b) 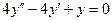 ;
c) ;
c) 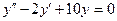 . .
| 8 .12. | a) 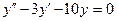 ;
b) ;
b) 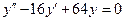 ;
c) ;
c) 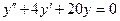 . .
|
| 8 .13. | a) 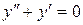 ;
b) ;
b) 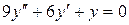 ;
c) ;
c) 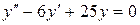 . .
| 8 .14. | a) 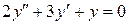 ;
b) ;
b) 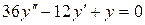 ;
c) ;
c) 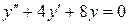 . .
|
| 8 .15. | a) 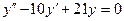 ;
b) ;
b) 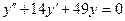 ;
c) ;
c) 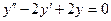 . .
| 8 .16. | a) 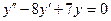 ;
b) ;
b) 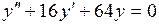 ;
c) ;
c) 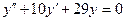 . .
|
| 8 .17. | a) 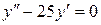 ;
b) ;
b) 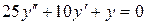 ;
c) ;
c) 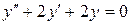 . .
| 8 .18. | a) 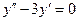 ;
b) ;
b) 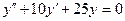 ;
c) ;
c) 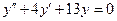 . .
|
| 8 .19. | a) 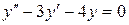 ;
b) ;
b) 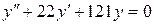 ;
c) ;
c) 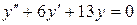 . .
| 8 .20. | a) 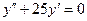 ;
b) ;
b) 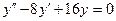 ;
c) ;
c) 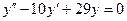 . .
|
| 8 .21. | a) 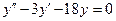 ;
b) ;
b) 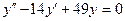 ;
c) ;
c) 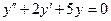 . .
| 8 .22. | a) 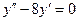 ;
b) ;
b) 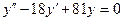 ;
c) ;
c) 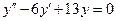 . .
|
| 8 .23. | a) 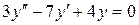 ;
b) ;
b) 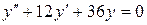 ;
c) ;
c) 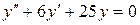 . .
| 8 .24. | a) 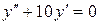 ;
b) ;
b) 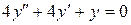 ;
c) ;
c) 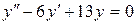 . .
|
| 8 .25. | a) 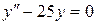 ;
b) ;
b) 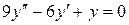 ;
c) ;
c) 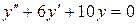 . .
| 8 .26. | a) 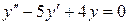 ;
b) y″−12y′−36y=0;
c) ;
b) y″−12y′−36y=0;
c) 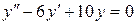 . .
|
| 8 .27. | a) 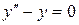 ;
b) ;
b) 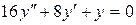 ;
c) ;
c) 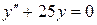 . .
| 8 .28. | a) 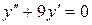 ;
b) ;
b) 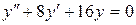 ;
c) ;
c) 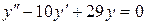 . .
|
| 8 .29. | a) 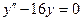 ;
b) ;
b) 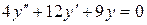 ;
c) ;
c) 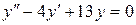 . .
| 8 .30. | a) 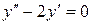 ;
b) ;
b) 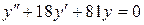 ;
c) ;
c) 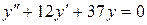 . .
|
9. Железнодорожная платформа массой m, выведенная из положения равновесия, совершает колебания в вертикальной плоскости под действием вынуждающей силы 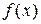 , где х — время. Найдите зависимость отклонения платформы от положения равновесия
, где х — время. Найдите зависимость отклонения платформы от положения равновесия 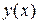 от времени, если сопротивление среды пропорционально скорости, с коэффициентом пропорциональности
от времени, если сопротивление среды пропорционально скорости, с коэффициентом пропорциональности 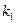 , а восстанавливающая сила рессоры, стремящаяся вернуть платформу в положение равновесия, пропорциональна величине отклонения, с коэффициентом пропорциональности
, а восстанавливающая сила рессоры, стремящаяся вернуть платформу в положение равновесия, пропорциональна величине отклонения, с коэффициентом пропорциональности 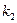 . Считается, что в момент времени
. Считается, что в момент времени 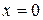 ,
, 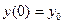 ,
, 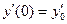 .
.
Таблица 3
| № | m | 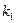
| 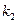
| 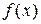
| 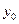
| 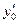
|
| 9.1 | 1 | -2 | 2 | 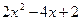
| 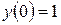
| 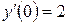
|
| 9.2 | 1 | -6 | 9 | 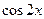
| 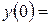 1 1
| 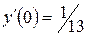
|
| 9.3 | 1 | -1 | 0 | 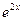
| 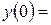 0 0
| 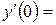 0 0
|
| 9.4 | 1 | 2 | -3 | 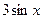
| 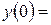 -0,3 -0,3
| 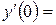 1 1
|
| 9.5 | 1 | 4 | 5 | 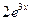
| 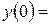 1 1
| 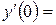 -1 -1
|
| 9.6 | 1 | 0 | -4 | 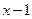
| 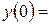 0 0
| 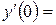 0 0
|
| 9.7 | 1 | 2 | 1 | 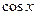
| 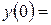 0 0
| 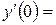 0 0
|
| 9.8 | 1 | -3 | -4 | 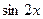
| 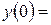 4 4
| 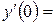 0 0
|
| 9.9 | 1 | 0 | -9 | 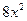
| 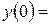 -2 -2
| 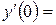 2 2
|
| 9.10 | 1 | 5 | 0 | 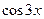
| 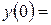 1 1
| 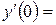 0 0
|
| 9.11 | 1 | -2 | 1 | 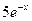
| 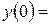 0 0
| 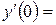 0 0
|
| 9.12 | 1 | 0 | 4 | 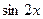
| 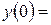 0 0
| 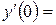 0 0
|
| 9.13 | 1 | 6 | -16 | 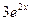
| 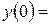 1 1
| 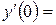 1 1
|
| 9.14 | 1 | 3 | 0 | 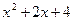
| 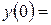 0 0
| 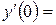 -1 -1
|
| 9.15 | 1 | -3 | -4 | 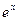
| 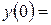 1 1
| 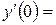 1 1
|
| 9.16 | 1 | -6 | 13 | 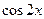
| 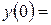 0 0
| 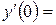 0 0
|
| 9.17 | 1 | 4 | 20 | 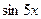
| 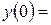 0 0
| 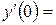 0 0
|
| 9.18 | 1 | 1 | 0 | 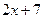
| 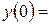 -2 -2
| 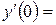 1 1
|
| 9.19 | 1 | 0 | -16 | 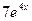
| 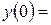 0 0
| 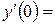 0 0
|
| 9.20 | 1 | -4 | 5 | 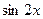
| 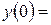 0 0
| 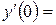 0 0
|
| 9.21 | 1 | 5 | -6 | 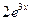
| 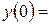 1 1
| 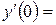 -1 -1
|
| 9.22 | 1 | 3 | -4 | 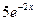
| 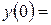 0 0
| 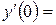 0 0
|
| 9.23 | 1 | 9 | 0 | 
| 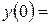 0 0
| 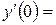 0 0
|
| 9.24 | 1 | 0 | 1 | 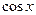
| 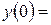 0 0
| 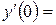 0 0
|
| 9.25 | 1 | 7 | -8 | 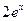
| 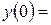 1 1
| 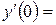 -1 -1
|
| 9.26 | 1 | -6 | 5 | 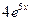
| 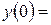 2 2
| 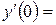 3 3
|
| 9.27 | 1 | -25 | 0 | 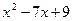
| 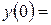 3 3
| 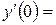 -1 -1
|
| 9.28 | 1 | 0 | 16 | 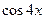
| 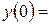 0 0
| 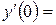 0 0
|
| 9.29 | 1 | -5 | 4 | 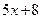
| 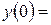 0 0
| 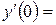 0 0
|
| 9.30 | 1 | 0 | 4 | 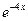
| 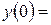 4 4
| 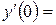 0 0
|
8. Дана система дифференциальных уравнений
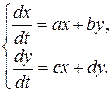
С помощью характеристического уравнения найти ее общее решение.
Таблица 4
| № | a | b | c | d | № | a | b | c | d |
| 10 .1 | -1 | 5 | 1 | 3 | 10 .2 | -2 | 1 | -3 | 2 |
| 10 .3 | 6 | 3 | -8 | -5 | 10 .4 | 2 | -1 | -6 | 3 |
| 10 .5 | 2 | 5 | 1 | -2 | 10 .6 | 6 | -1 | 3 | 2 |
| 10 .7 | -7 | 5 | 4 | -8 | 10 .8 | -1 | 2 | -3 | 4 |
| 10 .9 | -1 | 1 | 2 | -2 | 10 .10 | -1 | -2 | 3 | 4 |
| 10 .11 | -1 | -2 | 1 | -4 | 10 .12 | -2 | 1 | 4 | 1 |
| 10 .13 | 3 | -2 | 1 | 0 | 10 .14 | 4 | 2 | 4 | 6 |
| 10 .15 | -5 | -8 | -3 | -3 | 10 .1 6 | 8 | -3 | 2 | 1 |
| 10 .17 | -4 | 2 | 4 | -2 | 10 .18 | 3 | 1 | 1 | 3 |
| 10 .19 | -3 | 6 | 2 | 8 | 10 .20 | 2 | 3 | 5 | 4 |
| 10 .21 | 2 | 1 | 3 | 4 | 10 .22 | 1 | 2 | 3 | 6 |
| 10 .23 | 1 | -1 | -4 | 1 | 10 .24 | 5 | 4 | 4 | 5 |
| 10 .25 | -1 | 8 | 1 | 1 | 10 .26 | 1 | -2 | -4 | 3 |
| 10 .27 | -2 | -3 | -1 | 0 | 10 .28 | 1 | -2 | -1 | 0 |
| 10 .29 | 1 | -1 | -4 | 4 | 10 .30 | 3 | -2 | 2 | 8 |
Примеры решения заданий контрольной работы № 6
ВЫСШАЯ МАТЕМАТИКА
Контрольные задания и примеры их решения для студентов
2 курса инженерно-технических специальностей
заочной формы обучения
Часть 3

Составители: Е. Н. Бесперстова
В. А.Гордеев
О. Ф. Маркович
Самара
| |
УДК 517
Высшая математика : контрольные задания и примеры их решения для студентов 2 курса инженерно-технических специальностей заочной формы обучения / составители : Е. Н. Бесперстова, В. А. Гордеев, О. Ф. Маркович. – Самара : СамГУПС, 2009. – 34 с.
Утверждены на заседании кафедры 02.03.09, протокол № 5.
Печатаются по решению редакционно-издательского совета университета.
Контрольные задания составлены в соответствии с Государственным образовательным стандартом и типовой программой по высшей математике и охватывают следующие разделы: неопределенный и определенный интегралы, дифференциальные уравнения, кратные и криволинейные интегралы.
Предназначены для студентов заочной формы обучения инженерно-технических специальностей.
Составители: ст.преп. Елена Николаевна Бесперстова
ст. преп. Владимир Александрович Гордеев
доц. Олег Филиппович Маркович
Рецензенты: к.т.н., доцент СГУ Г. В. Воскресенская;
к.т.н., доцент СамГУПС Ю. В. Гуменникова
Под редакцией к.т.н., доц. В. П. Кузнецова
Подписано в печать 08.12.2009. Формат 60×90 1/16.
Усл. печ. л. 2,1. Заказ № 230.
| |
Дата: 2018-11-18, просмотров: 674.