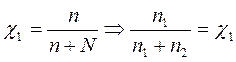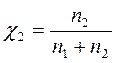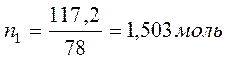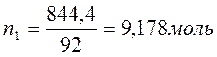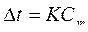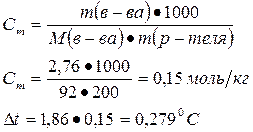План занятия
1. Проверка посещаемости и информация
2. Программированный контроль и опрос
3. Решение типовых задач
4. Практическое построение диаграмм состояния бинарных систем. Определение по диаграммам:
- состава смеси
- характеристических точек
- числа степеней свободы в любой точке и области диаграммы
5. Подведение итогов занятия
Контрольные вопросы и задания по теме занятия
1. Фазовое равновесие раствор-пар растворителя. Закон Рауля. Определение. Математическое выражение.
2. Следствия из закона Рауля. Определение. Математическое выражение.
3. Понятие об идеальных смесях.
4. Диаграмма "давление-состав" для идеальных смесей.
5. Формула для расчета состава пара в идеальных смесях (вывод).
6. Первый закон Коновалова. Математическое обоснование.
7. Расширенный вариант диаграммы "давление-состав".
8. Диаграмма "температура-состав" для идеальных смесей.
9. Правило рычага. Определение. Математическое выражение.
10. Неидеальные смеси. Положительное и отрицательное отклонение от закона Рауля.
11. Второй закон Коновалова. Азеотропные смеси.
12. Анализ диаграммы азеотропной смеси с положительным отклонением от закона Рауля (отрицательным отклонением).
13. Диаграммы плавкости, когда компоненты неограниченно растворимы и в жидком и в твердом состоянии. Линия ликвидуса. Линия солидуса.
14. Диаграммы плавкости, когда компоненты взаимно нерастворимы в твердом состоянии. Линии ликвидуса, солидуса. Точка эвтектики.
15. Правило рычага Определение относительного количества твердой и жидкой фаз.
16. Применение диаграмм плавкости.
17. Простая перегонка.
18. Фракционная перегонка. Ректификация.
19. Особенности жидких смесей с взаимно нерастворимыми жидкостями. Перегонка с водяным паром.
а). Основная литература:
1. Физическая и коллоидная химия [Текст]: учеб. пособие для вузов / А.П. Беляева [и др.]. - М., ГЭОТАР – Медиа, 2010.– 130 – 137, 140 – 156, 168 – 170 с.
Эталоны решения типовых задач
Расчет молярной доли компонента в растворе, парциального давления компонентов, общего давления пара над раствором
Задача 1
Бензол и толуол образуют идеальный раствор при 30ºС, давление чистого бензола 15705 Па и толуола 4661 Па. Для раствора, содержащего 117,2 г бензола и 844,4 г толуола определить: мольные доли компонентов в растворе; парциальные давления компонентов; общее давление пара над раствором; мольные доли компонентов в паре.
| Дано: Р01 = 15705 Па Р02 = 4661Па m1 = 117,2 г m2 = 844,4 г |
Решение:
M(бензола C6H6) =78 г/моль;
M(толуола C6H5-СН3) =92 г/моль;
|
| Р1 = ? Р2 = ? Робщ = ? χ1 = ? χ2 = ? |
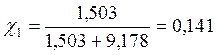
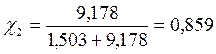
Р1 = χ1Р01 = 0,141 • 15705 = 2214,4 Па
Р2 = χ2Р02 = 0,859 • 4661 = 4003,8 Па
Робщ = Р1 + Р2 = 2214,4 + 4003,8 = 6218,2 Па
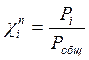- мольная доля компонента i в паре
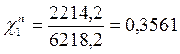
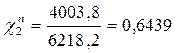
Таким образом в паре повышается содержание более летучего компонента – бензола (1), т.к. по условию Р01>Р02
Расчетные задачи на I и II законы Рауля
Задача 2
Определить давление насыщенного пара над водным раствором сахарозы, моляльная концентрация которого равна 0,2 моль/кг, если давление насыщенного пара чистой воды равно 24 мм.рт.ст.
| Дано: Сm = 0,2 моль/кг Р0 = 24 мм.рт.ст. | Решение: Сm = 0,2 моль/кг означает, что 0,2 моль сахарозы содержится в 1 кг H2O, т.е. n = 0,2 моль |
| Р = ? |
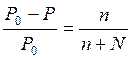
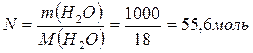
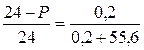
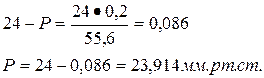
Ответ: 23,914 мм.рт.ст.
Задача 3.
На сколько понизится температура замерзания раствора, если 2,76 г глицерина С3Н5(ОН)3 растворить в 200 г воды (Кводы=1,86)?
| Дано: m(в-ва) = 2,76 г m(Н2О) = 200 г Кводы=1,86 |
Решение:
Ответ: 0,279ºC |
| ∆tзам = ? |
Эталоны решения задач по диаграммам состояния
Задача 4
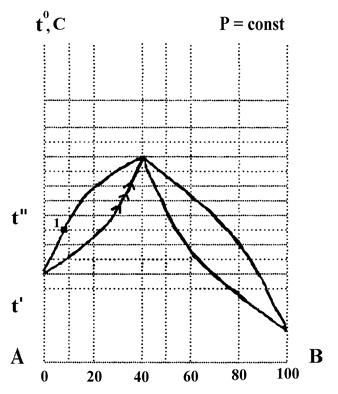
По диаграмме состояния компонентов А и В, построенной в координатах температура кипения - состав (см. рис. 1), определить:
1. К какому типу относится данная система?
2. Что представляет собой система состава 80% А и 20% В при температуре t'. Какими степенями свободы она обладает?
3. При какой температуре начнется кипение этой системы? Каким компонентом будет обогащаться пар, образующийся при ее кипении?
4. На какие составляющие можно разделить исходную систему ректификацией?
5. Как называют смесь состава 60% А и 40% В? Какими свойствами она обладает?
Рис. 1. Диаграмма “Температурного кипения – состав” компонентов А и В
Решение:
1. Изображенная диаграмма характерна для неограниченно смешивающихся жидкостей.
2. Система представляет собой гомогенную жидкость (раствор). По правилу фаз: С = К – Ф + 1 = 2 – 1 + 1 = 2, т.е, произвольно можно задавать температуру и состав.
3. Кипение системы начнется при t''. Пар будет обогащаться компонентом А. Его состав: 90% А и 10% 3 (точка 1).
4. Жидкая фаза будет обогащаться компонентом В и ее температура кипения будет непрерывно расти. Изменение состава жидкой фазы при кипении изображено на рисунке стрелками.
5. Так как пар обогащается компонентом А, а жидкость компонентом В, то при ректификации в паровой фазе можно получить чистый компонент А, а в жидкой - азеотропную смесь.
6. Смесь состава: 60% А и 40% В называют азеотропной (или нераздельнокипящей). Такая смесь имеет экстремальную температуру кипения (в данном примере – максимальную). При кипении образуется пар такого же состава, как и состав жидкой фазы. Поэтому азеотропную смесь нельзя разделить на компоненты ректификацией при постоянном давлении.
Задача 5
По диаграмме плавкости системы компонентов А - В (см. рис. 2), которая построена в координатах температура - состав в массовых процентах, определить.
К какому типу относится данная система?
Что представляет собой система состава 80% А + 20% В при температуре t', какими степенями свободы она обладает?
При какой температуре начнется кристаллизация в этой системе? Какое вещество (компонент) будет кристаллизоваться при этой температуре?
Как будет изменяться состав системы при медленном охлаждении и при какой температуре закончится кристаллизация? Каковы состав и весовое количество фаз первоначальной системы, если провести ее резкое охлаждение до температуры t''', общий вес системы принять равным 1 кг. Какими степенями свободы обладает система в этом состоянии?
Что представляет собой система и какими степенями свободы она обладает при температуре t''''?
Решение:
1. Изображенная на диаграмме система относится к таким системам, которые образованы веществами, неограниченно растворимыми в жидком состоянии и нерастворимыми в твердой состоянии.
2. Система заданного состава характеризуется фигуративной точкой а. Она представляет собой гомогенную (однофазную) систему – раствор (расплав). Согласно правилу фаз С = К – Ф + 1 = 2 – 1 + 1 = 2, т.е. в однофазном состоянии произвольно можно изменять температуру и состав системы.
Рис. 2 Диаграмма плавкости компонентов А и В
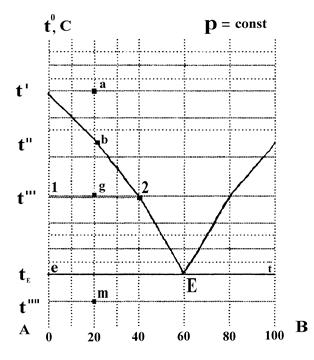
3. Кристаллизация компонента А начнется при температуре t''. Состав этой кристаллической фазы можно найти по изотерме (точка b). Кристаллизация компонента А приведет к увеличению в растворе содержания компонента В, а, в связи с этим, к понижению температуры кристаллизации компонента А по линии bE. Кристаллизация компонента А будет продолжаться до температуры tE. В точке Е состав жидкой фазы: 40% А и 60% В. Из такой жидкой фазы при дальнейшем охлаждении кристаллизуются оба компонента А и В (им соответствуют точки е и t). При этом температура не изменяется и в равновесии сосуществуют кристаллы А, кристаллы В и жидкая фаза (точка Е называется эвтектической точкой). В этом состоянии система не имеет степеней свободы (С = 0), поэтому температура кристаллизации остается постоянной до тех пор, пока не исчезнут последние капли жидкой фазы. После этого твердая фаза, состоящая из кристаллов А и В, будет охлаждаться.
4. При резком охлаждении системы до t''' (точка g) состав жидкой фазы значительно изменится вследствие выпадения кристаллов компонента А. Составы равновесных фаз можно найти, используя термическое условие фазовых равновесий. Точка 1 определяет состав твердой фазы (компонент А), точка 2 - состав равновесной жидкой фазы (60% А и 40% В): из точки 2 опускают перпендикуляр и определяют состав жидкой фазы. По диаграмме состояния можно не только определить состав находящихся в равновесии фаз, но и оценить их относительное и абсолютное количество, Для этой цели служит правило рычага, согласно которому:
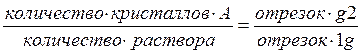
В рассматриваемом состоянии системы при температуре t''' общий (валовый) состав системы 80% А и 20% В, а в жидкой фазе 60% А и 40% В. Принимая общий вес 1 кг, получим:
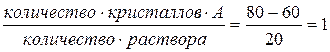
т ,е, вес кристаллов А и раствора одинаковые (по 0,5 кг).
При t''' система, заданная точкой a, имеет одну степень свободы (можно произвольно менять либо температуру, либо состав).
5. При t'''' в системе нет жидкой фазы. Точка m характеризует гетерогенную двухфазную систему, содержащую 20% В и 80% А, система имеет одну степень свободы (С = 1), которой может быть только температура, так как компоненты в твердом виде не образуют растворов и понятие «концентрация» теряет смысл.
Задача 6
По диаграмме состояния компонентов А и В, построенной в координатах: температура смешения - состав (см. рис. 3) определить:
Рис. 3 Диаграмма состояния системы ограниченно растворимых компонентов А и В с нижней критической температурой смешения
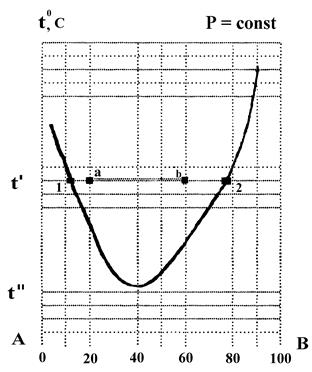
1. К какому типу относится данная система?
2. Что представляет собой система состава: 80% А и 20% В при температуре t'? Какими степенями свободы она обладает?
3. Каков состав равновесных фаз при температуре t'?
4. Как изменяется растворимость с понижением температуры?
5. Что представляет собой исходная система при температуре t'', какими степенями свободы она обладает?
6. Какие изменения произойдут в системе при температуре t'', если содержание компонента А изменится от 80% до 40%.
Решение:
1. Изображенная диаграмма характерна для ограниченно-смешивающихся жидкостей с нижней критической температурой смешения.
2. Заданная система характеризуется фигуративной точкой а.
3. При температуре t' - она двухфазна. Составы фаз можно определить по точкам пересечения изотермы с кривыми растворимости (точки 1 и 2). Число степеней свободы С = 2 - 2 + + 1 = 1, т.е. произвольно можно задавать или температуру или концентрацию насыщенных растворов.
4. Составы фаз: фаза компонента А (точка 1) содержит 90% А и 10 % В; фаза компонента В (точка 2) содержит 20% А и 80% В
5. С понижен ней температуры растворимость компонентов растет.
6. При температуре t'' система состава 80% А и 20% В становится однофазной и обладает двумя степенями свободы, т.е., произвольно можно задавать температуру и концентрацию.
7. При содержании компонента А - 40 % (фигуративная точка b) система остается двухфазной. Составы фаз не изменяются (они определяются точками 1 и 2), изменится весовое соотношение между фазами.
Эталон построения диаграммы состояния, нахождение характеристических точек
Задача 7
Дана зависимость составов жидкой фазы и находящегося с ней в равновесии пара от температуры для двухкомпонентной жидкой системы А - В при постоянном давлении.
А - Н2О; В - С3Н8О – пропанол
| Молярный состав В, % | ж.ф | 0 | 20 | 40 | 60 | 80 | 90 | 100 |
| пар | 0 | 40 | 57 | 60 | 70 | 75 | 100 | |
| Т, ºС | 100 | 95,0 | 90,8 | 87,7 | 89,2 | 91,5 | 97,8 | |
1. Построить диаграмму кипения Н2О - С3Н8О в координатах “Т - состав”. Определить тип бинарной смеси.
2. Определить точки, соответствующие равновесию фаз одинакового состава. Описать их качественный и количественный состав (точки А, Б, В).
3. Рассчитать число степеней свободы в точках А, Б, В и точке ХВ, соответствующей 40 % С3Н8О, при Т1 = 94ºС.
Для системы, содержащей ХВ = 40 % С3Н8О, определить:
4. Температуру начала кипения системы (т. 4)
5. Состав первой капли конденсата (пара) над этой системой (т. 5).
6. Температуру конца кипения (т. 6).
7. Состав последней капли жидкой фазы (т. 7).
8. Состав и массу пара и жидкой фазы при Т1 = 94 ºС, если масса всей системы равна 2 кг.
Решение:
1. Для построения диаграммы состояния необходимо определить масштаб по оси абсцисс - ось состава и ось ординат - ось температур.
Состав изменяется от 0 до 100 % или от 0 до 1 мольных долей, значит ось абсцисс надо разделить на 10 одинаковых частей (1 деление = 10 % или 0,1 мольная доля).
В нашем случае интервал температур ∆Т = Тmax - Tmin = 100 - 87 = 13 ºС. Удобно взять также 10 делений (1 деление = 2 ºС), начиная с 80 ºС.
Нанести деления на оси координат согласно выбранного масштаба.
При построении диаграммы кипения надо знать, что каждой температуре, кроме температур кипения чистых жидкостей, соответствует две точки, определяющие состав жидкой фазы и состав равновесного с ней пара.
На ось ординат наносим точки, соответствующие температуре кипения чистых жидкостей: т.А Ткип = 100 ºС Н2О и т.Б Ткип = 97,8 ºС С3Н8О. Для каждой температуры мысленно проводим горизонталь и отмечаем точки, соответствующие содержанию компонента В (С3Н8О) в жидкой фазе и паре разными символами, например ▲ и ●. Последовательно соединяя точки, соответствующие составу жидкой фазы, получаем линию жидкости; соединяя точки, соответствующие составу пара - линию пара.
Диаграмм кипения “Т - состав” для системы Н2О - С3Н8О с положительным отклонением от закона Рауля (рис.4).
Рис. 4 Диаграмма кипения “Т - состав” для системы Н2О - С3Н8О
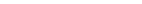
2. Равновесию фаз одинакового состава соответствуют точки:
| т. А - температура кипения H2O | ТА = 100 ºС | 100 % H2O в жидкой фазе и паре |
| т. Б - температура кипения С3Н8О | ТБ = 97,8 ºС | 100 % С3Н8О в жидкой фазе и паре |
| т. В - температура кипения азеотропной смеси | ТВ = 87,7 ºС = min | состав 60 % С3Н8О и 40 % H2O в жидкой фазе и паре |
3. Число степеней свободы для диаграммы состояния “Т - состав” рассчитывают по уравнению Гиббса С = К - Ф + 1, т.к. они построены при условии P = const.
Для т. А и Б:
К = 1 чистые С3Н8О или H2O
Ф = 2 жидкость и пар
С = 1-2+1 = 0 система нонвариантна
Для т. В - азеотропная смесь, состав жидкой и газообразной фаз одинаков, поэтому считаем, что смесь ведет себя как чистое вещество: К = 1, Ф = 2, С = 1-2+1 = 0
Для т. 1, где ХВ = 40 %, при Т1 = 94 ºС:
К = 2 чистые С3Н8О и H2O
Ф = 2 жидкость и пар
С = 2-2+1 = 1
4. Смесь, содержащая 40 % С3Н8О начнет кипеть при Т4 = 90,8ºС (т. 4).
5. Состав первой капли конденсата (пара) при Т = 90,8 ºС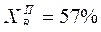 
С3Н8О (т. 5).
6. Смесь закончит кипение при Т = 95 ºС (т. 6).
7. Состав последней капли жидкости при Т = 95 ºС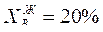 
С3Н8О (т. 7).
8. Массу пара и жидкости при Т = 94 ºС можно определить по правилу рычага.
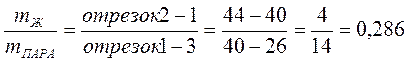
Обозначим mЖ = х
mПАРА=2 - х, т.к. общая масса смеси равна 2 кг
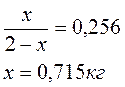
Масса жидкой фазы mЖ = 0,715 кг, состав (т. 2) 44 % С3Н8О и 56 % H2O.
Масса пара mПАРА = 2 - 0,715 = 1,285 кг, состав пара (т. 3) 26 % С3Н8О и 74 % H2O.
Задачи для самостоятельной работы
1. Чему равно давление насыщенного пара над 10%-ным водным раствором карбамида СО(NН2)2 при 100º С, если давление пара над чистым растворителем 101,09 кПа?
2. При 25º С давление насыщенного пара воды составляет 3,166 кПа. Найти при той же температуре давление насыщенного пара над водным раствором мочевины СО(NН2)2, если ω (СО(NН2)2) = 5%.
3. Каково давление пара 10%-ного водного раствора сахара С12H22O11 при 100ºС, если давление пара чистого растворителя 760 мм.рт.ст.?
4. Давление насыщенного пара над раствором с массовой долей Na2SO4, равно 10 %, при 40ºС равно 7,1 кПа, а давление насыщенного пара над водой при этой температуре равно 7,4 кПа. Рассчитайте степень электролитической диссоциации сульфата натрия в долях единицы.
5. При 100º С давление пара раствора, содержащего 0,05 моль сульфата натрия в 450 г воды, равно 100,8 кПа. Определить степень диссоциации Na2SO4, если давление пара над чистым растворителем 101,3 кПа?
6. Давление пара водного раствора с массовой долей NaNO3 8% равно 2,26 кПа при 20º С. Давление паров воды при этой температуре равно 2,34 кПа. Найдите кажущуюся степень диссоциации (в процентах) нитрата натрия в этом растворе.
7. Раствор 0,455 г тироксина в 10 г бензола замерзает при температуре 5,144º С, тогда как температура замерзания чистого бензола 5,444º С. Какова молекулярная масса тироксина, если криоскопическая постоянная бензола К(С6Н6) = 5,12.
8. Определите молекулярную массу вещества – неэлектролита, если при растворении 0,9 г его в 50 г воды получен раствор с температурой кипения 100,052º С. Эбуллиоскопическая постоянная воды равна 0,52.
9. Если 10 г глюкозы С6H12O6, растворить в 400 г этилового спирта, температура кипения спирта повышается на 0,1428º С. При растворении 2 г неизвестного органического вещества в 100 г этилового спирта температура кипения повышается на 0,125º С. Вычислите молярную массу неизвестного вещества.
10. Раствор, содержащий 5 г вещества в 100 г воды, кипит при 100,42º С. Найти молекулярную массу этого вещества, зная, что электрический ток раствор не проводит. Еводы = 0,52.
11. После растворения 0,412 г нафталина (С10Н8) в 10 г камфары температура замерзания раствора оказалась на 13º С ниже по сравнению с температурой замерзания чистой камфары. Чему равна криоскопическая константа для камфары, рассчитанная на основании этих данных?
12. Температура кипения раствора, содержащего 12 г гидроксида натрия в 100 г воды, равна 102,65º С. Рассчитайте степень электролитической диссоциации NaOH в этом растворе в процентах. Эбуллиоскопическая постоянная воды равна 0,52.
13. Многовариантная задача
Дана зависимость составов жидкой фазы и находящегося с ней в равновесии пара от температуры для двухкомпонентной жидкой системы А - В при постоянном давлении.
1. Построить диаграмму кипения А - В в координатах “Т - состав” и определить ее тип.
2. Определить точки, соответствующие равновесию фаз одинакового состава. Описать их качественный и количественный состав (точки А, Б, В).
3. Рассчитать число степеней свободы в точках А, Б, В и точке ХВ при Т1 (т. 1).
Для системы, содержащей ХВ, определить:
4. Температуру начала кипения системы (т. 4)
5. Состав первой капли конденсата (пара) над этой системой (т. 5).
6. Температуру конца кипения (т. 6).
7. Состав последней капли жидкой фазы (т. 7).
8. Массу пара и жидкой фазы при Т1, если масса всей системы равна 2 кг.
|
№ |
Система
Молярный состав В, %
Т, К
ХВ
Т1
Занятие № 8
Дата: 2018-12-21, просмотров: 671.
