2.2.1. Общая характеристика механических
элементов автоматики
Сегодня большинство математических операций в аналоговых системах управления выполняются с помощью электромеханических элементов. Однако существуют механические элементы, которые трудно и нецелесообразно заменять другими, например, электромеханическими или электронными. Такими элементами являются дифференциалы, эксцентрики, коноиды, графики. Они широко применяются в конструкции корабельных навигационных систем и систем управления оружием.
Механические счетно-решающие устройства отличаются высокой надежностью работы. Они малочувствительны к влиянию температуры и влажности, устойчиво регулируются в течении длительного периода эксплуатации. Их точность определяется тщательностью изготовления, сборки, регулировки и в известных пределах может быть повышена за счет увеличения их размеров. В некоторых случаях использование механических элементов дает значительное сокращение габаритов приборов при решении сложных функций. Все эти положительные качества механических счетно-решающих устройств определили целесообразность их применения в корабельных системах.
Но счетно-решающим устройствам с механическими элементами присущи и недостатки. Это, прежде всего, большие габариты и вес, значительная инерционность, сложность изготовления, а отсюда и высокая стоимость.
Механические счетно-решающие устройства являются моделями, в которых заданные математические зависимости, исходные данные и вырабатываемые величины изображаются в виде линейных и угловых механических перемещений. Это изображение должно производиться в определенном масштабе. Масштаб показывает, сколько единиц изображаемой навигационной величины содержится в одной единице линейного (углового) перемещения ведущего или ведомого звена (детали). Масштаб КХ определяется по формуле
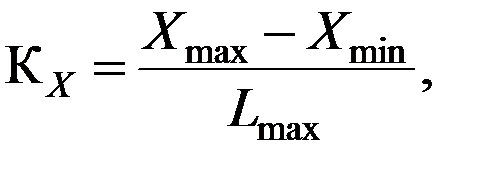(2.1)
где 
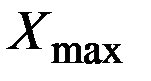и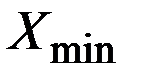 
- максимальное и минимальное значения изображаемой величины;
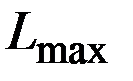- максимальное линейное перемещение звена счетно-решающего устройства.
Если, например, в счетно-решающем устройстве требуется воспроизвести величину дистанции Д (заданную пределами Д = 0-180кбт) линейным перемещением детали 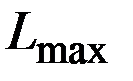= 100 мм, то масштаб дистанции
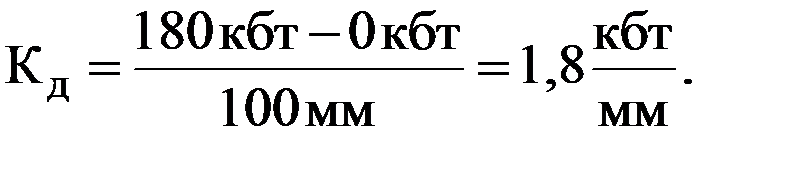
Если заданная величина в счетно-решающем устройстве моделируется углом поворота детали (вала), то вместо понятия «масштаб» часто пользуются понятием «цена оборота».
Под ценой оборота детали понимают число единиц математической величины, соответствующее одному полному обороту детали (вала). Цена оборота детали А определяется по формуле
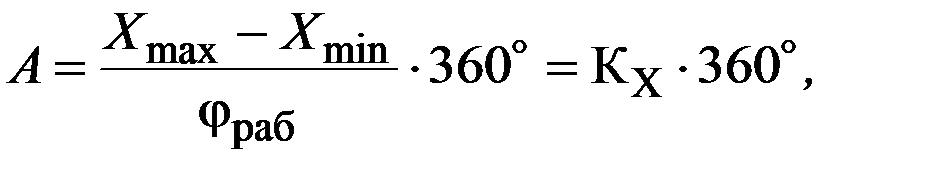(2.2)
где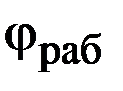 
- рабочий угол поворота детали счетно-решающего устройства;
КХ - масштаб величины X, определяемый по формуле, аналогичной (2.1).
Если рабочий угол детали счетно-решающего устройства jраб = 0-60°, то для нашего примера
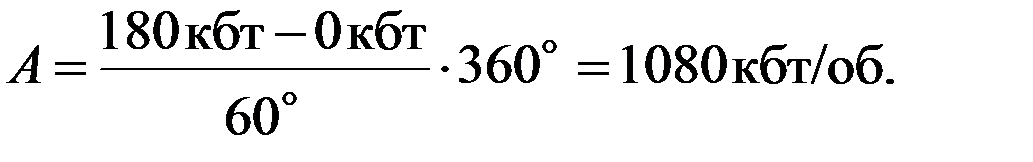
Здесь:
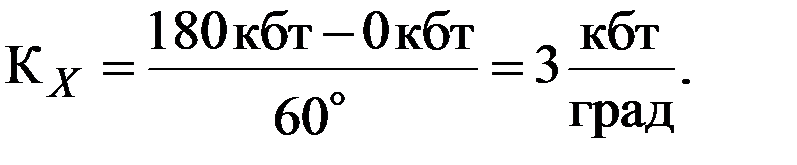
2.2.2. Механические вычислительные устройства
Из механических решающих устройств в морских средствах навигации применяются:
- механические дифференциалы, моделирующие математическую задачу алгебраического сложения;
- конусные фрикционные механизмы, используемые для интегрирования, умножения или деления;
- кулачковые механизмы, которые подразделяются на:
- эксцентриковые механизмы, применяемые для получения сложной нелинейной функции одной переменной;
- коноидные механизмы, предназначенные для моделирования сложной функции двух переменных.
Механический дифференциал схематично изображен на рис. 2.3.
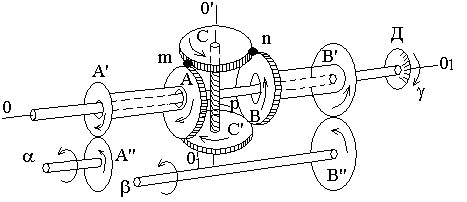
Рис. 2.3. Механический зубчатый дифференциал:
(А, В – планетарные колеса; Д – шкала; Р – водило; С – сателлиты)
Основными частями дифференциала являются: два планетарных конических зубчатых колеса А и В, имеющих равное число зубцов Z1 и Z2; валик со шкалой Д, который жестко связан с водилом Р; два конических зубчатых колеса (сателлиты) – С. Планетарные колеса свободно вращаются на валике, ось которого направлена по линии ОО1. Сателлиты С, находясь в зацеплении с планетарными колесами А и В, свободно вращаются на водиле Р, ось которого направлена по линии ОО1. Для ввода углов α и β, пропорциональных определенным математическим величинам, служат соответственно шестерни A¢ и A² , жестко соединенные с планетарным колесом А, и шестерни В¢ и В², также жестко скрепленные с планетарным колесом В. Шкала-шестерня Д жестко укреплена на валике и служит для съема величины угла, пропорционального алгебраической сумме углов α и β.
Фактически при одновременном развороте планетарных колес А и В соответственно на углы α и β, шкала Д валика механического дифференциала (рис. 2.3) развернется на угол γ, определяемый выражением
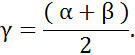
Цены оборотов шкал планетарных колес А и В должны быть в 2 раза меньше цены шкалы оборота валика со шкалой Д. Например, механический дифференциал, применяемый в автопрокладчике АП-4, используется для моделирования формулы определения текущего значения счислимой широты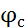 
плавания корабля на любой момент времени:
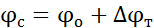
где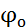 
– начальная широта при включении АП-4;
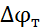– текущее приращение широты, рассчитываемое в счетно-решающем устройстве автопрокладчика АП-4.
В автопрокладчиках применяется и другое механическое вычислительное устройство − конусный фрикционный механизм (рис. 2.4), используемый для моделирования операций умножения или деления.
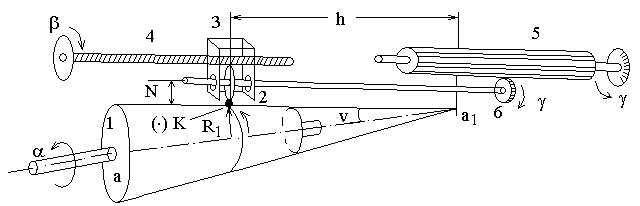
Рис. 2.4. Конусный фрикционный механизм
(1 – конус; 2 – ролик; 3 – каретка; 4 – винт; 5 – зубчатый валик; 6 – шестерня)
В состав фрикционного механизма входят: усеченный конус; угол между образующей и осью вращения, который равен ν; ролик, имеющий радиус вращения r; каретка, перемещение которой вместе с роликом вдоль образующей конуса осуществляется с помощью винта; зубчатый валик, на который передается вращение ролика с помощью укрепленной на его оси шестерни. Допустим, что после разворота винта на угол b каретка с роликом переместилась в такое положение, что расстояние от вершины конуса а1 до точки соприкосновения K ролика с конусом вдоль его образующей стало равно величине h . При повороте конуса на угол α с угловой скоростью ωk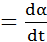 
ролик, вследствие наличия трения между ним и конусом, развернется на угол γ с угловой скоростью ωp 
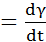. А так как радиусы шестерни и зубчатого валика одинаковы, то и шкала будет развернута на угол γ.
Уравнение движения конусного фрикционного механизма имеет вид
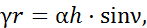(2.3)
где γ – угол разворота ролика и шкалы зубчатого валика;
r – радиус ролика;
α – угол разворота конуса;
h – перемещение каретки от вершины конуса до точки касания конуса и ролика, пропорциональное углу b разворота
винта;
n – угол при вершине конуса между его образующей и осью вращения.
Анализируя уравнение (2.3), видим, что данная схема моделирует математическую операцию умножения. Действительно, если смещение h будет пропорционально одному сомножителю, а угол поворота α – другому, то при условии
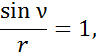
получим
γ = ha.
Рассмотренный механизм можно использовать также и для операции деления. Для этого в роли делимого должен выступать угол поворота ϒ ролика, а делителем являться смещение h. Тогда (при соблюдении условия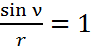 
)
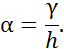
Конусный фрикционный механизм также может работать и в качестве интегрирующего устройства. Для этого конус должен вращаться с постоянной угловой скоростью ωk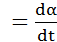 
.Тогда угол разворота ролика и шкалы зубчатого валика γ определится как:
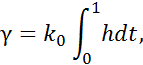
где k0 = ωk (при соблюдении условия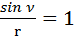 
).
Подобное устройство используется в относительных лагах для получения пройденного кораблем расстояния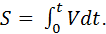 
При этом ролик должен быть механически связан со счетчиком, фиксирующим значение угла α, тогда смещение h каретки будет соответствовать значению интегрируемой величины.
Счетно-решающие устройства, воспроизводящие функции от одной и двух переменных. Характерная особенность многих механических элементов состоит в том, что каждое из них может реализовать только очень ограниченный класс функций. Действительно, дифференциалы можно использовать только для алгебраического суммирования двух величин; синусно-косинусные построители воспроизводят только тригонометрические функции.
Рассмотрим механические элементы, обладающие более широкими возможностями: они воспроизводят самые различные функции одной или двух переменных. Применение этих устройств в ряде случаев значительно упрощает автоматическую реализацию заданной функции, например, при воспроизведении в системе сложной функции двух переменныхw и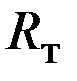 
вида
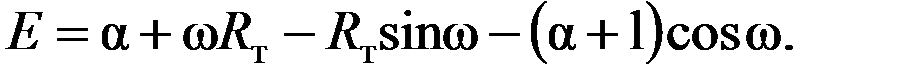
Одно из подобных устройств - коноид -заменяет совокупность суммирующих, множительных и синусно-косинусных механизмов.
Кроме того, некоторые счетно-решающие устройства могут быть использованы также для воспроизведения табулированных функциональных зависимостей, т. е. зависимостей, заданных не аналитически, а таблично.
Кулачковые механизмы. Кулачковыми механизмами называются такие механизмы, у которых основным элементом является плоский кулачок (эксцентрик) или пространственный кулачок (коноид).
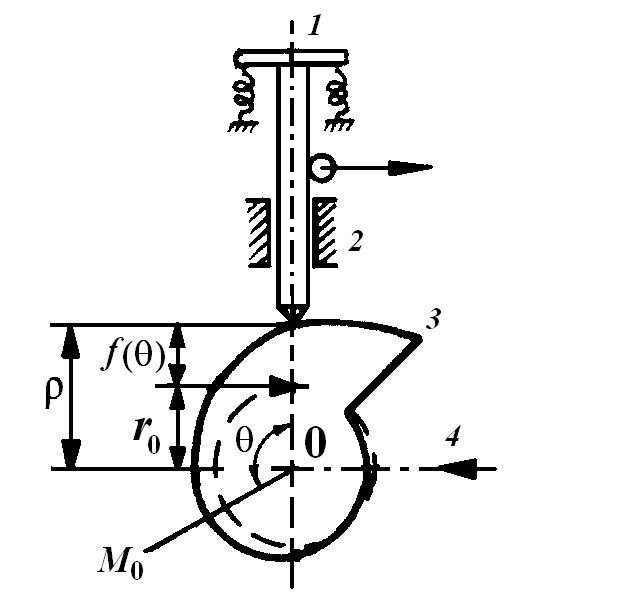
Рис.2.5. Эксцентриковый механизм
Кулачком называется твердое тело 3, закономерно очерченная рабочая поверхность которого приводит в движение соприкасающееся с ним второе тело, называемое щупом 1 (рис.2.6). Закон движения щупа1зависит от очертания кулачка3.
Кулачковые механизмы, как правило, используются в качестве корректирующих устройств, когда какой-либо НП необходимо исправить поправкой, определяемой экспериментально или рассчитываемой по сложной нелинейной формуле. Так, например, эксцентриковый механизм используется в магнитном компасе типа КДЭ-П для ввода поправки в магнитный курс за девиацию, которая определяется во время девиационных работ на каждом магнитном курсе.
Эксцентриковый механизм дает возможность на основании известного значения аргумента найти его функцию. Математически эта зависимость выражается в общем виде так:
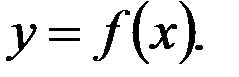
Функция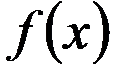 
может быть весьма сложной и трудно реализуемой с помощью других счетно-решающих устройств.
Щуп 1 механизма несет зубчатую рейку и перемещается в направляющих2. Постоянство соприкосновения конца щупа с рабочей поверхностью эксцентрика достигается с помощью пружин.
Коноидный механизм предназначен для автоматической выработки функции двух переменных, т.е. решения математической зависимости вида
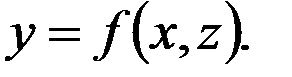
Коноидный механизм (рис.2.7) состоит из следующих элементов: тела коноида1, каретки5, щупа2 и зубчатой передачи3, предназначенной для снятия выработанной функции. Щуп прижимается к телу коноида пружиной4.
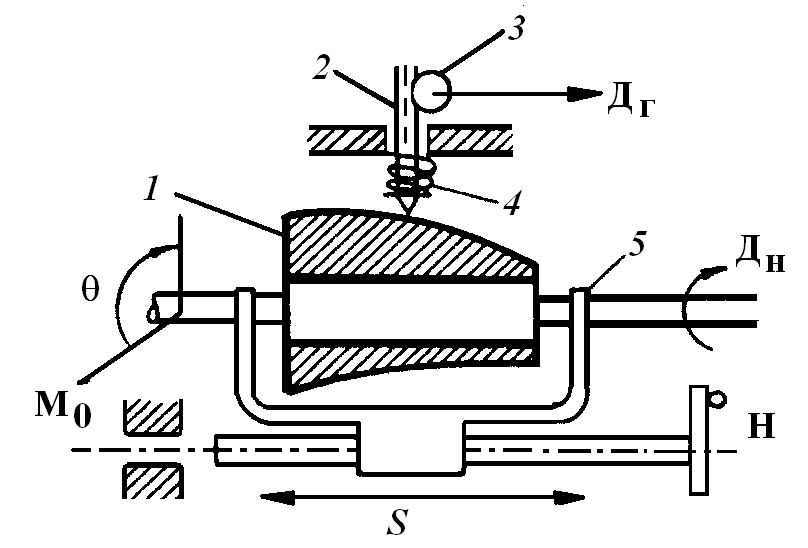
Рис. 2.6. Коноидный механизм
Перечисленные элементы коноидного механизма собраны в корпусе. Тело коноида можно представить как набор эксцентриков, насаженных на один вал, начальные радиусы которых равны. Если число этих эксцентриков увеличивать, а толщину их уменьшать до бесконечности, то в пределе получим гладкую поверхность тела коноида, воспроизводящую функцию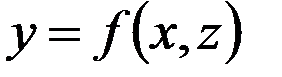 
. Поверхность тела коноида в этом случае может быть описана выражением
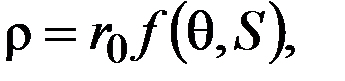
где
r – радиус-вектор точки поверхности тела коноида;
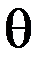– угол поворота тела коноида, которым задается один из аргументов, например, х;
S – перемещение каретки со щупом вдоль тела коноида пропорционально второму аргументу z.
Искомая функция определится величиной перемещения щупа в плоскости, перпендикулярной оси коноида, следовательно
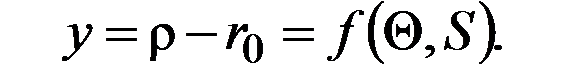
Дифференцирующие и интегрирующие счетно-решающие устройства. Дифференцирующие и интегрирующие устройства служат для дифференцирования и интегрирования различного рода функций, изменяющихся во времени.
Производная функция Z по времени t представляет собой, как известно, скорость ее изменения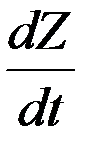 
. Поэтому дифференцирующие устройства называются тахометрами или измерителями скорости.
В большинстве случаев операции дифференцирования и интегрирования выполняют одни и те же устройства, и они рассматриваются в одном параграфе.
В корабельных системах практическое применение из этого типа счетно-решающих устройств получили графические тахометры.
Графический тахометр. Графический тахометр применяется для дифференцирования главным образом функций, меняющихся во времени не плавно, а прерывно, дискретно (например, для определения скорости изменения координат цели, измеряемых гидролокационными станциями или оптическими дальномерами). Принцип действия его основан на известном положении о том, что производная функции в точке касания равна тангенсу угла a, который образует касательная в этой точке с положительным направлением оси абсцисс.
Схема графического тахометра изображена на рис.2.7. В состав механизмов, воспроизводящих график функции 
, входят следующие основные элементы: бумажная лента 1, намотанная на валики2 и 5 и движущаяся с постоянной скоростью, бесконечная металлическая лента 3, перекинутая через валики 4 и 10 с закрепленными на ней бойками-отметчиками, печатающее магнитное устройство. Для определения производной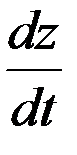 
как тангенса угла наклона касательной к графику функции служат: стеклянный диск 9 с нанесенными на нем параллельными линиями, ходовой винт 8 с гайкой 7 и рычагом 6, представляющие собой тангенсный механизм.
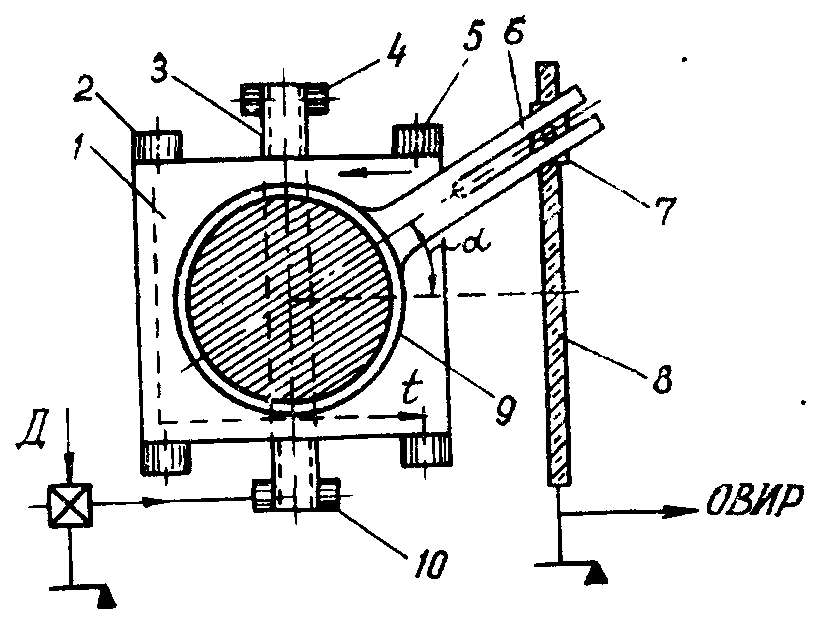
Рис. 2.7. Графический тахометр
Отсчетные механизмы. Отсчетные механизмы в корабельных системах служат для фиксации и снятия отсчетов численных значений наблюдаемых величин.
Основными элементами отсчетного механизма являются шкала с делениями и индекс, имеющие возможность смещаться относительно друг друга. По геометрической форме шкалы бывают линейные и круговые. В зависимости от этого подвижный элемент механизма - шкала или индекс - совершает либо поступательное движение, либо вращательное. В счетно-решающих устройствах распространены круговые дисковые шкалы (рис. 2.8). Индекс отсчетного механизма может быть выполнен в виде стрелки, штриха или нити.
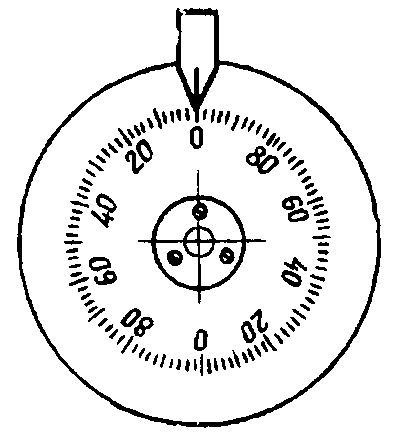
Рис. 2.8. Дисковые шкалы
Основные требования, предъявляемые к отсчетным механизмам, сводятся к удобству и достаточной точности отсчета, возможности регулировки. Шкалы располагают так, чтобы они были легко доступны наблюдению. В целях удобства отсчета цена делений выбирается всегда в округленных цифрах, например, 0.25, 0.5, 1, 2, 5 и т. д. единиц. Как правило, против пятых, десятых и т.д. делений цифрами проставляются значения считываемой или устанавливаемой величины. Например, 0, 5, 10, 15, ... . В тех случаях, когда наблюдаемая величина может принимать положительные и отрицательные значения (курсовой угол корабля), цифры, отвечающие тем или другим значениям, выполняются различным цветом, например, красным и зеленым.
Для удобства отсчета расстояние между двумя соседними делениями (длина интервала И) должно быть не менее 1-1,5 мм.
Для обеспечения возможности регулирования отсчетного механизма стрелки и вращающиеся шкалы устанавливают на валиках с помощью регулировочных муфт.
Точность отсчета по шкале определяется ценой наименьшего деления t. Если индекс расположен между делениями, то отсчет берут, как правило, соответствующим ближайшему делению. Наибольшая возможная погрешность в значении величины X, снимаемой со шкалы, при этом равна
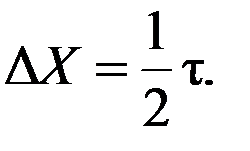
Если делений на шкале много, то, чтобы повысить точность установки и отсчета данных, применяют механизмы с двумя шкалами-шкалой грубого отсчета и шкалой точного отсчета. Шкала точного отсчета выполняется с расчетной ценой деления tТ.О. = t, где t = 2DX, со сравнительно небольшим числом делений nТ.О. и ценой оборота
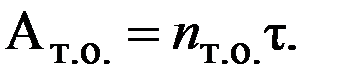
Цена деления шкалы грубого отсчета tГ.О. выбирается кратной цене оборота шкалы точного отсчета, отсюда
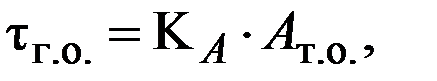
где KА - коэффициент кратности.
Например, если дистанция изменяется в пределах 0-2800м, t = 1 м, то удобно принять:
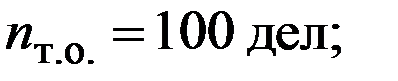
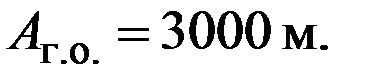
Тогда
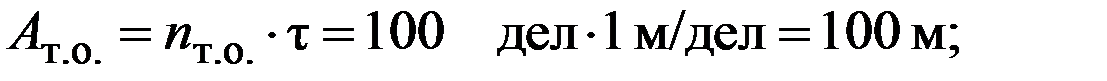
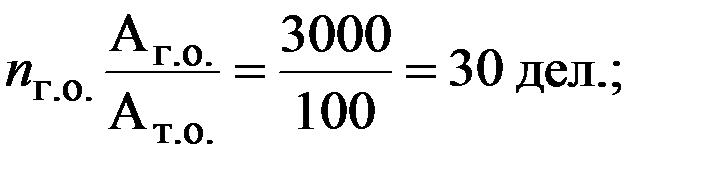
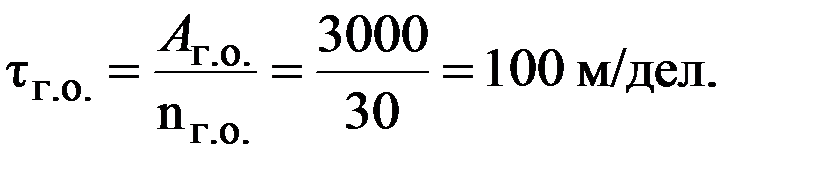
Контрольные вопросы
1. В чем достоинства и недостатки механических элементов автоматики?
2. Что такое «приборное моделирование»? Приведите определение (или формулу) масштаба моделирования.
3. Как соотносятся понятия «масштаб» и «цена оборота вала»?
4. Назначение и устройство механического дифференциала. Какие типы дифференциалов Вы знаете?
5. Какие кулачковые механизмы Вы знаете? В чем их различие?
6. В каких случаях используется тахометр? Значение слова «тахометр».
7. Приведите примеры отсчетных механизмов
8. Какие методы повышения точности отсчетных механизмов Вы знаете?
9. В чем особенности оцифровки шкал?
10. Приведите формулы расчета числа делений и цены оборота шкалы грубого отсчета в двухотсчетных шкалах.
Дата: 2018-12-21, просмотров: 534.
