Для решения сложных задач требуется несколько счетно-решающих устройств, которые собираются в виде вычислительной машины. Вычислительные машины непрерывного действия состоят из целого ряда отдельных блоков, каждый из которых служит для выполнения одной какой-либо математической операции (сложения, вычитания, умножения, деления, интегрирования, образования заданной функции и т.д.). Эти блоки с помощью кинематических, электрических или других связей соединяются в последовательности, каждая из которых отвечает конкретному виду решаемого уравнения. Если вычислительная машина предназначается для решения уравнений только одного вида, то состав вычислительных устройств и их соединений между собой постоянны.
Вычислительные устройства непрерывного действия для решения задач воспроизводят физический процесс, описываемый уравнениями, подобными математическим зависимостям, подлежащим решению. Условились формулу, описывающую математическую операцию, подлежащую воспроизведению с помощью вычислительного устройства непрерывного действия (счетно-решающего устройства), называть моделируемой формулой; а формулу, описывающую связь в счетно-решающем устройстве, моделирующей формулой. Главным условием использования какого-либо устройства в качестве счетно-решающего является подобие моделирующей и моделируемой формул. В этом смысле вычислительные устройства непрерывного действия являются математическими моделями изучаемых процессов или задач. Поэтому эти устройства и машины называются моделирующими или аналоговыми.
Достоинствами вычислительных устройств непрерывного действия являются сравнительная простота их конструкции, а также возможность решать задачи в реальном масштабе времени. Поэтому вычислительные устройства непрерывного действия всё ещё довольно широко применяются в корабельных системах управления.
К недостаткам вычислительных устройств непрерывного действия следует отнести, прежде всего, ограниченную точность вычисляемых результатов. Точность вычислений, производимых этими устройствами, зависит от качества изготовления отдельных узлов, принятых при изготовлении допусков, а также от температуры окружающей среды. Кроме того, в некоторых электрических устройствах точность зависит от колебаний напряжения и частоты питающего тока.
В устройствах дискретного действия переменные и постоянные величины представляются в виде определенного цифрового кода. Основой таких устройств является цифровая вычислительная машина (ЦВМ). Решение задачи в ЦВМ сводится к определенной последовательности арифметических действий и логических операций, задаваемых программой. Переход от решения одной задачи к решению другой осуществляется путем смены программы без изменения структуры машины.
Основными преимуществами вычислительных устройств дискретного действия, или цифровых вычислительных устройств, перед устройствами непрерывного действия являются универсальность и значительно большая точность вычислений.
Универсальность ЦВМ позволяет на кораблях один и тот же тип машины использовать для решения целого комплекса задач (например, задач кораблевождения, применения ракетного или торпедного оружия и т.д.).
Недостатками устройств дискретного действия являются необходимость создания специальных устройств-преобразователей типа «вал-число» и «код-аналог», которые преобразуют непрерывные величины в цифровые и обратно и позволяют сопрягать ЦВМ с объектами управления. Кроме того, они требуют принятия специальных мер защиты от электрических помех естественного и искусственного происхождения.
По характеру выполняемых задач вычислительные устройства делятся на универсальные и специализированные.
Универсальные вычислительные устройства, как правило, дискретного действия. Они служат для решения широкого круга задач по заранее разработанной программе, которая вводится в устройство перед началом работы.
Специализированные вычислительные устройства - устройства дискретного или непрерывного действия, предназначенные для решения задач определенного типа или класса, имеющих ограниченную область применения (например, СЦВМ «Карат» в НК «Симфония») .
По назначению вычислительные устройства делятся на вычислительные и управляющие.
Вычислительные устройства предназначены для решения задач, связанных с получением некоторых числовых величин. Наиболее типичными примерами таких устройств являются центральные решающие приборы систем СУ противолодочным оружием.
Управляющие устройства представляют собой специализированные машины непрерывного или дискретного действия. Они обрабатывают поступающую информацию, а результаты обработки используются для управления различными подвижными объектами (СЦВМ «Карат»).
По месту установки вычислительные устройства делятся на корабельные (береговые) и бортовые.
Счетно-решающие устройства также можно классифицировать по роду физического явления, положенного в основу их функционирования, а также по характеру выполняемых операций.
По роду физического явления, положенного в основу функционирования, СРУ делятся на:
- механические;
- электромеханические;
- электронные.
В механических СРУ при решении математических зависимостей исходные данные задаются параметрами, характеризующими перемещения ведущих звеньев механизма (валиков, шестеренок, реек), а результаты решения- параметрами перемещения ведомых звеньев этого механизма. К механическим СРУ относятся дифференциалы, эксцентриковые и коноидные механизмы, фрикционные механизмы и др.
В электромеханических СРУ, по крайней мере, одна входная или выходная величина задается или вырабатывается в виде механического перемещения или угла поворота. К электромеханическим СРУ относятся потенциометры, сельсины, вращающиеся трансформаторы, тахогенераторы и т. д.
Электронные СРУ представляют собой устройства, основанные на электронных элементах: электронных лампах, полупроводниковых элементах, электронно-лучевых трубках и др. В них входные и выходные величины задаются в виде электрических напряжений (токов).
По характеру выполняемых операций СРУ делятся на:
- суммирующие;
- множительные (выполняющие операции умножения и деления);
- дифференцирующие и интегрирующие;
- функциональные (воспроизводящие функции одного или нескольких аргументов);
- устройства для тригонометрических преобразований.
Требования, предъявляемые к элементам
Автоматики
Основными требованиями являются требование точности работы элементов автоматики и их надежность.
Решение задач корабельными приборами должно производиться с точностью, которая обеспечила бы максимальную эффективность их боевого применения. Поскольку сегодня основу этих приборов составляют счетно-решающие устройства, то к ним предъявляется требование - обеспечить необходимую точность выполняемых операций.
Точностью элемента или счетно-решающего устройства называется степень приближения реализованного им значения математической зависимости к истинному ее значению. Мерой точности работы счетно-решающего устройства может служить абсолютная ошибка (погрешность) или приведенная относительная погрешность.
Абсолютная погрешность представляет собой разность между значением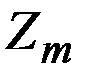 
реализованным устройством, и истинным значением Z соответствующей математической или физической величины:
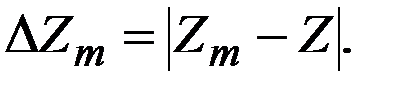
Относительная погрешность определяется соотношением
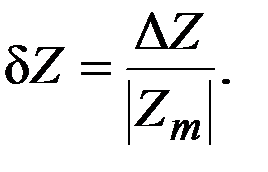
При решении навигационных задач зачастую важно знать знак ошибки, поэтому в этом случае под абсолютной ошибкой понимают разность:
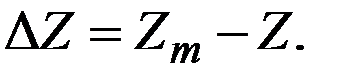
По своему характеру ошибки делятся на систематические и случайные. Систематические ошибки обусловливаются определенными причинами, которые могут быть всегда устранены или достаточно точно учтены. Случайные ошибки вызываются, как правило, многими отдельными причинами, действующими в каждом конкретном случае по-разному. Полностью исключить эти ошибки невозможно, их учесть можно только в среднем, для чего необходимо знать законы распределения случайных ошибок.
Полная погрешность результата, получающаяся на выходе счетно-решающего устройства, обычно представляется следующими составляющими:
- трансформированной ошибкой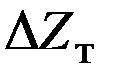 
, являющейся результатом погрешностей в значениях входных величин счетно-решающего устройства;
- методической ошибкой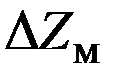 
, являющейся результатом отступлений моделирующей формулы от моделируемой;
- инструментальной ошибкой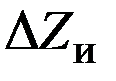 
, вызванной несовершенством изготовления счетно-решающего устройства.
Ошибки входных величин счетно-решающего устройства являются следствием ошибок измерения или ошибок ввода, которые по своей природе являются случайными. Поэтому и трансформированные ошибки являются случайными величинами. Если ошибки входных данных подчиняются закону нормального распределения (что справедливо в абсолютном большинстве случаев), то закону нормального распределения подчиняются и трансформированные ошибки. Поэтому их определяют по правилам преобразования нормально распределенных величин.
Если в приборе решается зависимость Z=Z(X, Y), где Х и Y – точные значения входных величин, то величина ошибки решения задачи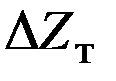 
, возникающей из-за ошибок входных аргументов DХ и DY, определяется по формуле
.
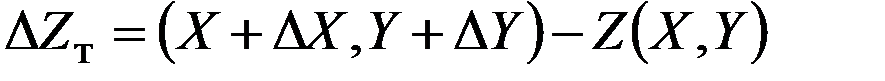Методическая ошибка является систематической ошибкой и поддается учету. Если вместо точного выражения
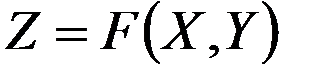
в счетно-решающем устройстве решается приближенное (такая замена применяется в целях упрощения конструкции счетно-решающего устройства) выражение
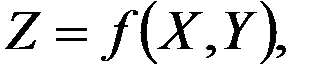
то методическая ошибка
.
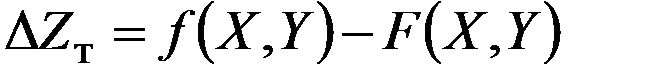Методическая ошибка рассчитывается на этапе проектирования системы с целью установить саму возможность использования этого упрощения в системе.
Инструментальная ошибка является случайной. В нее входят различные допуски и отклонения при изготовлении, износ деталей, люфт, отклонения напряжений и емкостей от номинальных значений и др. Инструментальная ошибка рассчитывается при проектировании счетно-решающего устройства применительно к конкретной схеме прибора с учетом масштабов и цен оборотов соответствующих звеньев.
Точность решения задачи счетно-решающими устройствами зависит также и от того, в каком масштабе представляются величины, участвующие в моделировании. Математические величины, участвующие в решении задачи, в счетно-решающем устройстве моделируются различными физическими величинами, а именно: механическими перемещениями, углом поворота, напряжением или силой тока и т. д. Коэффициенты пропорциональности, связывающие в счетно-решающем устройстве переменные математические величины и соответствующие им физические величины, называются масштабами этих величин.
Если переменная величина X, имеющая размерность линейной величины (например, метр), воспроизводится физической величиной U в вольтах, то масштаб величины Х определяется выражением
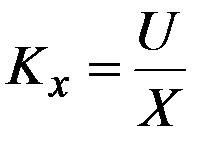, (В/м)
Масштаб показывает, сколько единиц физической величины, используемой для построения модели, соответствует одной единице моделируемой величины. Чем больше масштаб, тем точнее воспроизводится моделируемая величина и результат моделирования.
Если математическая величина моделируется вращательным движением некоторой детали счетно-решающего устройства, например, поворотом ротора индукционной электрической машины, то в качестве масштаба может быть использована цена оборота. Под ценой оборота понимают число единиц масштабируемой величины, соответствующее полному обороту детали.
Надежность систем автоматики - это способность сохранять наиболее существенные свойства на заданном уровне в процессе эксплуатации. Для надежной работы системы необходимо использовать элементы, обладающие хорошими показателями надежности. Это особенно важно в связи с возрастающим многообразием систем автоматики, применением их для выполнения очень ответственных задач. Но чем сложнее эти системы, чем большее число элементов они содержат, тем больше появляется причин для снижения надежности. Возникает противоречие: чем ответственнее и сложнее задача, выполняемая системой автоматики, тем меньше может оказаться надежность этой системы. Основными путями преодоления этого противоречия являются следующие:
- повышение надежности элементов автоматики;
- разработка методов создания надежных систем, состоящих из ненадежных элементов;
- разработка систем контроля, предупреждающих и обнаруживающих отказы;
- разработка методов обслуживания сложных систем.
Основным термином в теории надежности является понятие «отказ». Отказами в работе элемента называют как выход из строя, так и изменение его параметров, приводящее к неудовлетворительному выполнению элементом его функций. Отказы, как правило, появляются внезапно, случайно, т. е. подчиняются законам, свойственным случайным величинам. Их изучают с помощью математической статистики. Для количественной оценки надежности элементов автоматики обычно используют следующие показатели:
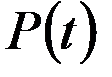- вероятность безотказной работы в течение заданного отрезка времени;
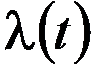- интенсивность отказов;
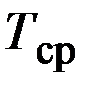- среднее время безотказной работы.
Основной количественной характеристикой надежности является вероятность безотказной работы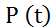 
- вероятность того, что за время t не произойдет отказа в работе. Эта величина может находиться в пределах от 0 до 1.
0 £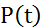 
£ 1.
На рис. 2.1 показан график функции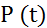 
.
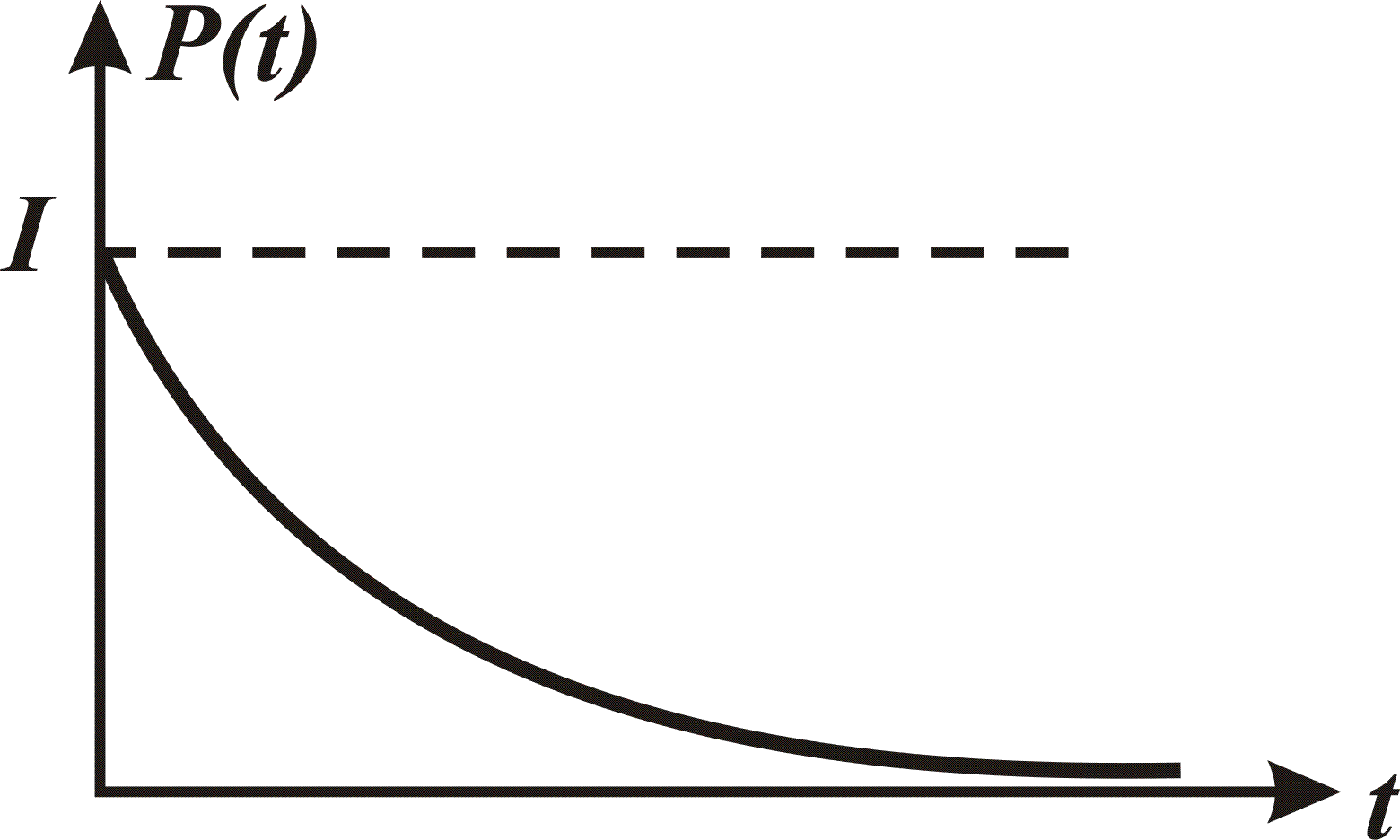
Рис. 2.1. Зависимость безотказной работы элемента от времени его
Работы
Вероятность безотказной работы элемента автоматики можно определить по результатам испытаний большого количества одинаковых элементов в течение заданного промежутка времени t
,
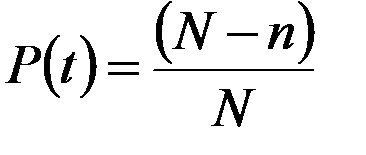где N - общее число испытанных элементов; п- число элементов, вышедших из строя за время испытаний.
Интенсивность отказов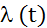 
или l-характеристика, очень часто используется для количественной оценки надежности элементов и при расчете надежности системы автоматики, состоящей из нескольких элементов. Величину l можно оценить как отношение числа отказавших элементов к числу оставшихся к данному моменту времени работоспособными элементов, взятое за единицу времени. Обычно единицей измерения интенсивности отказов является число отказов в час. Типичная кривая интенсивности отказов в зависимости от времени эксплуатации для большого числа однотипных элементов, изготовленных на одном и том же заводе по одинаковой технологии, приведена на рис. 2.2.
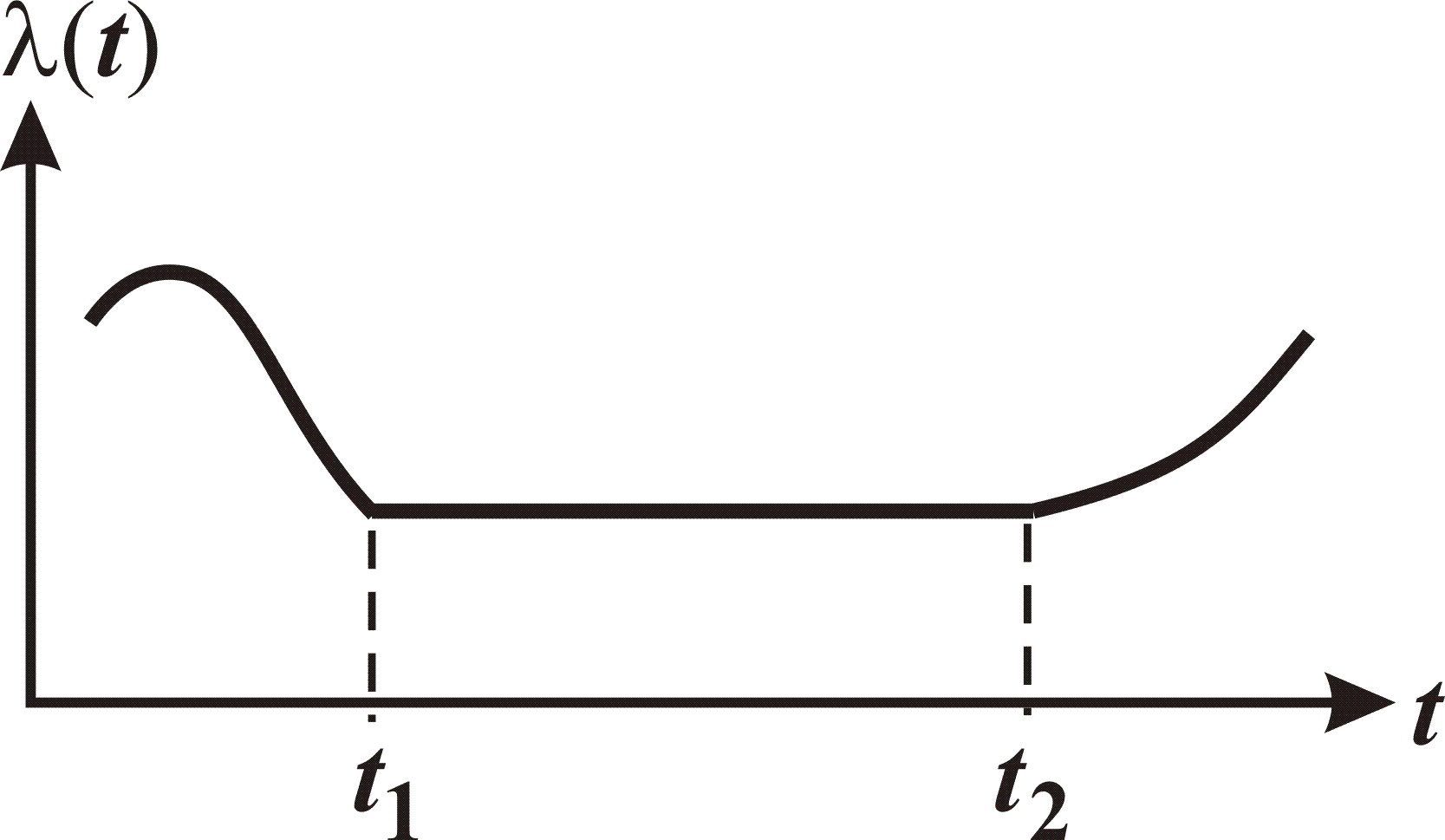
Рис. 2.2. Типичная зависимость интенсивности отказов от времени
На этой кривой можно выделить три характерных участка. Первый участок от 0 до t1 - называют периодом приработки и тренировки элемента. В этот период выходят из строя некачественно изготовленные элементы. Обычно этот период проходит на заводе-изготовителе, дорожащем своей репутацией. Дефектные элементы заранее, как говорится, «выжигают», а не пускают в продажу. Второй участок (от t1 до t2) - это период нормальной эксплуатации элемента, в течение которого интенсивность отказов низкая и примерно постоянная. На этом участке вероятность безотказной работы определяется по формуле
.
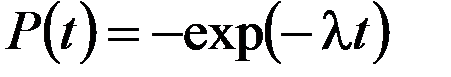Третий участок начинается с момента 
и характеризуется нарастанием интенсивности отказов, что объясняется старением и износом элементов. Обычно рекомендуется произвести замену элементов до наступления момента времени .
Среднее время безотказной работы при постоянной интенсивности отказов определяется очень просто:
.
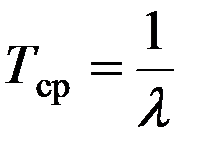Следует отметить, что на величину интенсивности отказов и соответственно на среднее время безотказной работы очень сильно влияют условия эксплуатации и качество технического обслуживания корабельной техники личным составом.
Контрольные вопросы
1. Назовите основные классификационные признаки, определяющие функциональную связь между входным и выходным сигналами.
2. Какие принципы классификации СРУ Вы знаете?
3. Типы ошибок СРУ.
4. Основные показатели надежности элементов автоматики.
Дата: 2018-12-21, просмотров: 323.
