Математической моделью звена является уравнение:
.
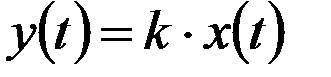где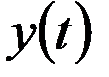 
и 
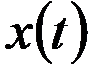- выходной и входной сигналы звена, являющиеся случайными функциями времени; 
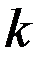- коэффициент усиления звена.
Преобразованное по Лапласу уравнение имеет вид:
.
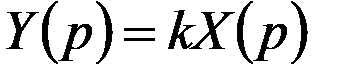Передаточная функция звена определяется из отношения
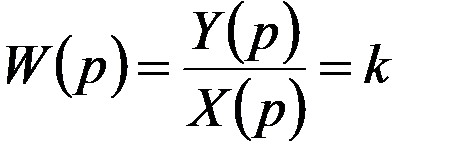
и представлена на рис. 1.8.
Идеальное звено является безинерционным, так как без переходного процесса изменяет входной сигнал в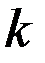 
раз.
Если на вход подается гармонический сигнал
,
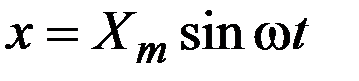то на выходе появится сигнал
,
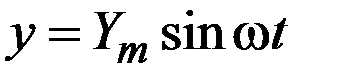где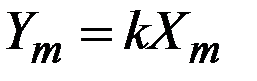 
.
В комплексной форме
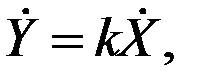
или
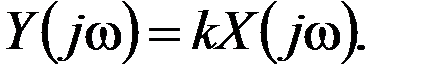
Тогда комплексный коэффициент усиления определится как
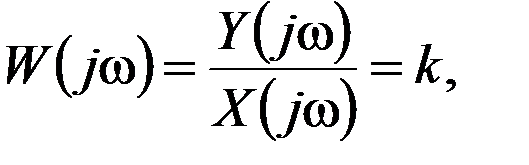
а переходная и импульсная функции для этого звена определятся как
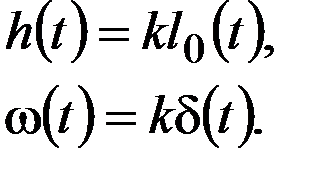
Примерами идеального звена могут служить делитель напряжения, усилитель постоянного тока, редукторная передача и др.
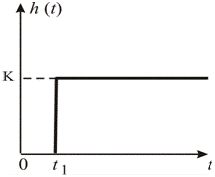
Рис. 1.8. Выходная характеристика идеального звена
Интегрирующее звено
В интегрирующем звене выходная величина пропорциональна или равна интегралу от входной величины, т.е.
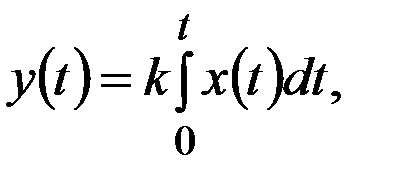
где k- некоторый коэффициент пропорциональности при одинаковой размерности входной и выходной величин. Он обратно пропорционален постоянной времени Т
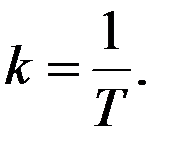
Дифференциальное уравнение интегрирующего звена имеет вид:
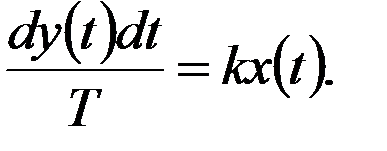
Преобразованное по Лапласу уравнение имеет вид:
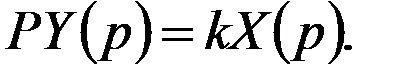
Передаточная функция звена определяется из отношения:
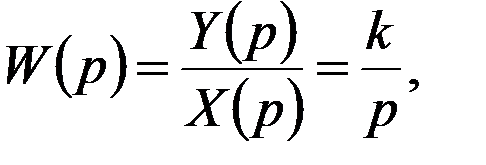
а при замене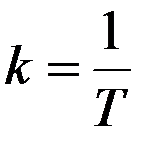 
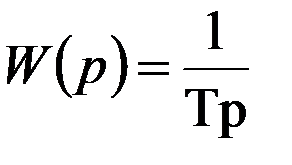
и представлена на рис. 1.9.
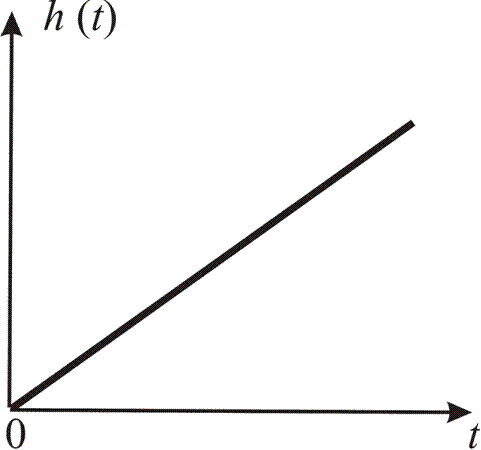
Рис. 1.9. Выходная характеристика интегрирующего звена
Если на вход подается гармонический сигнал
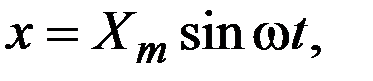
то на выходе появится сигнал
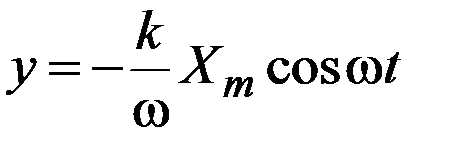
ил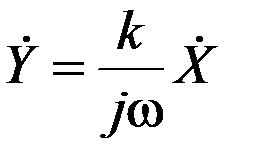и
и 
Тогда комплексный коэффициент усиления определится как
,
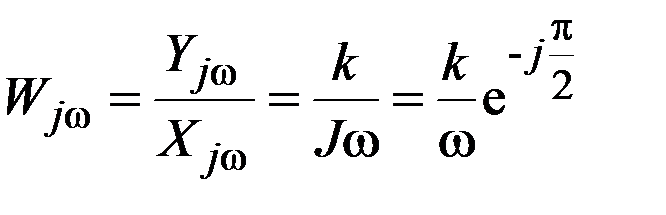а переходная и импульсная функции для этого звена определятся как:
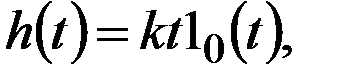
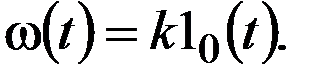
Примерами интегрирующего звена могут служить электрическая емкость, индуктивность, вращающийся вал и др.
Дифференцирующее звено
Уравнение дифференцирующего звена:
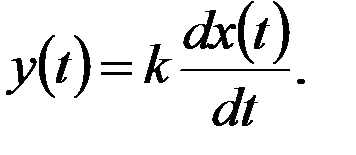
Преобразованное по Лапласу уравнение имеет вид:
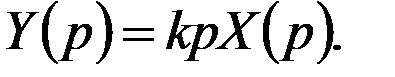
Передаточная функция определяется из отношения
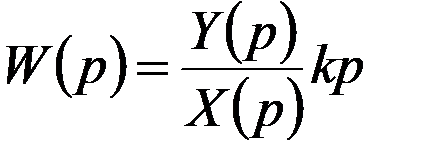
и представлена на рис. 1.10.
Рис. 1.10. Выходная характеристика дифференцирующего звена
Комплексный коэффициент усиления звена определится как
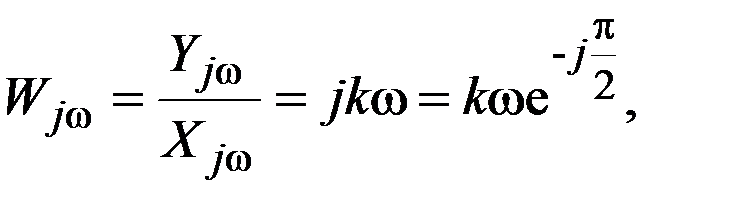
а переходная и импульсная функции для этого звена определятся как
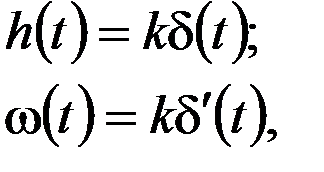
где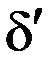 
- производная от дельта-функции.
Примерами дифференцирующего звена могут служить электрическая емкость, электрический тахометр и др.
Апериодическое звено
Уравнение апериодического звена:
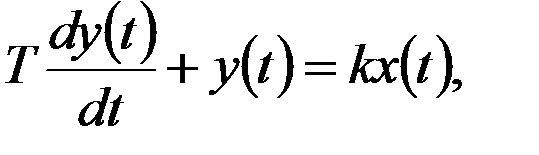
где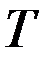 
- постоянная времени, характеризующая инерционность звена; 
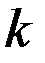- коэффициент его усиления.
Преобразованное по Лапласу уравнение имеет вид:
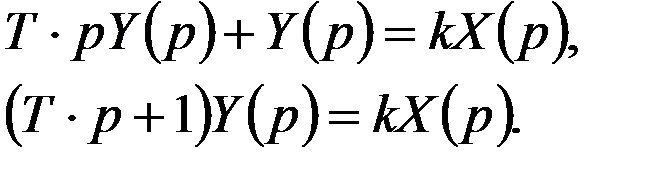
Передаточная функция звена определяется из отношения
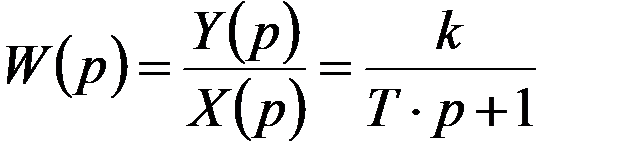
и представлена на рис. 1.11.
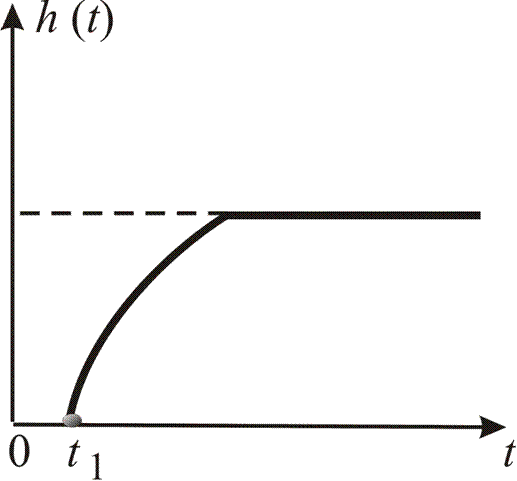
Рис. 1.11. Выходная характеристика апериодического звена
Постоянная времени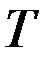 
показывает, что преобразование в звене сопровождается переходным процессом.
Комплексный коэффициент усиления определится как
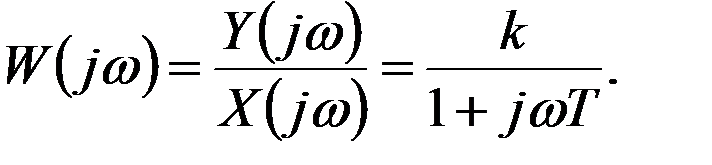
а переходная и импульсная функции для этого звена определятся как
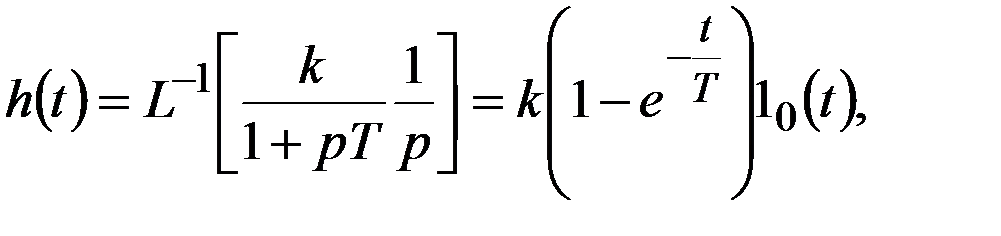
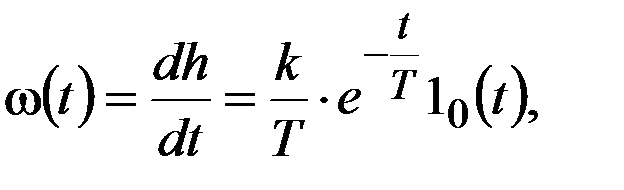
Примерами инерционного звена могут служить электронные и магнитные усилители, четырехполюсники, содержащие индуктивности или емкости, а также генератор и двигатель.
Колебательное звено
Уравнение колебательного звена записывается уравнением второго порядка:
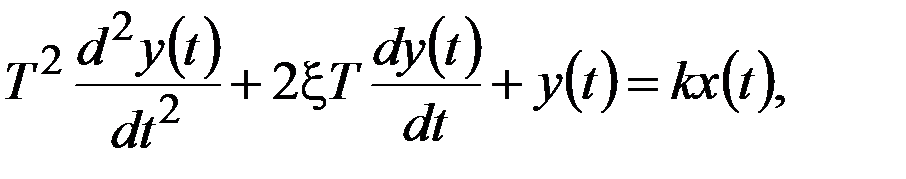
где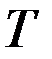 
-постоянная времени; 
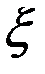-относительный коэффициент затухания; 
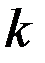- коэффициент преобразования.
Преобразованное по Лапласу уравнение имеет вид:
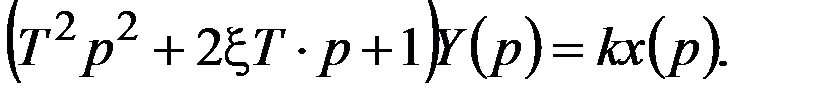
Передаточная функция определяется из отношения
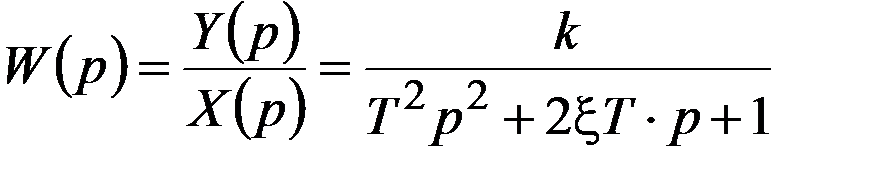
и представлена на рис. 1.12.
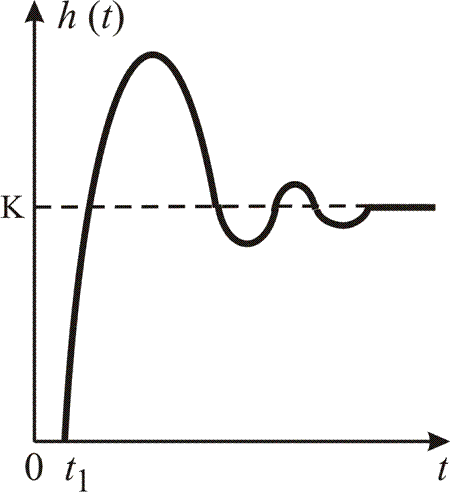
| Рис. 1.12. Выходная характеристика колебательного звена |
1.2.3. Структурные схемы САР
При изображении схем систем управления применяются два подхода – функциональный и структурный и, соответственно, схемы подразделяются на функциональные и структурные.
Функциональной схемой называется схема, в которой каждому функциональному элементу системы соответствует звено определенного типа.
Структурной схемой называется схема, в которой каждой математической операции должно соответствовать вполне определенное звено.
С точки зрения теории автоматического регулирования механические, электрические и другие элементы, различные по физической природе, но описываемые одинаковыми линейными дифференциальными уравнениями, являются одинаковыми звеньями. Однако, в зависимости от полноты математического описания и от математических операций, выполняемых одним и тем же функциональным звеном, описывающим объекты различной природы, их структурные схемы могут различаться.
Структурная схема составляется из типовых звеньев с известными передаточными функциями. Звено изображают прямоугольником, в котором указывают передаточную функцию. На звено может воздействовать только одна входная величина.
Передаточная функция системы при последовательном соединении (рис. 1.13) звеньев равна произведению передаточных функций этих звеньев.
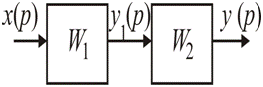
Рис. 1.13.Схема последовательного соединения типовых звеньев
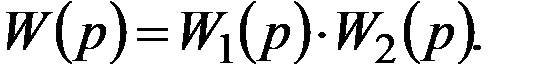
И если
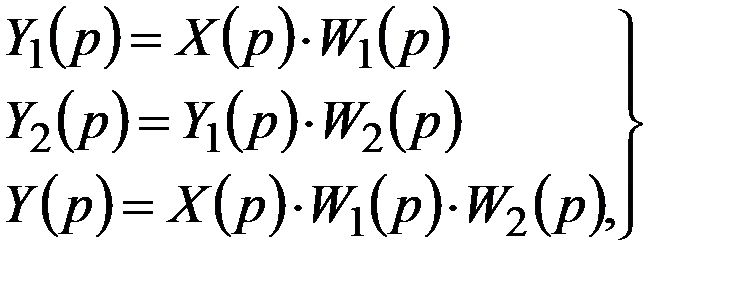
то
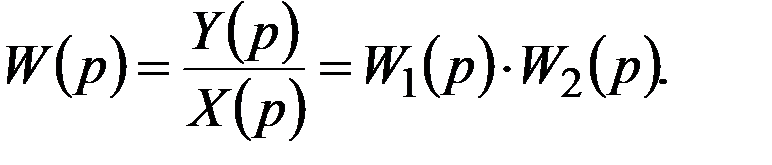
Передаточная функция системы при параллельном соединении звеньев (рис. 1.14), равна сумме передаточных функций этих звеньев:
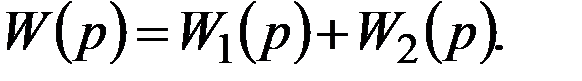
Если
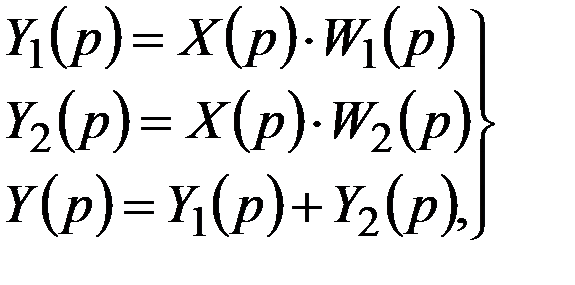
то
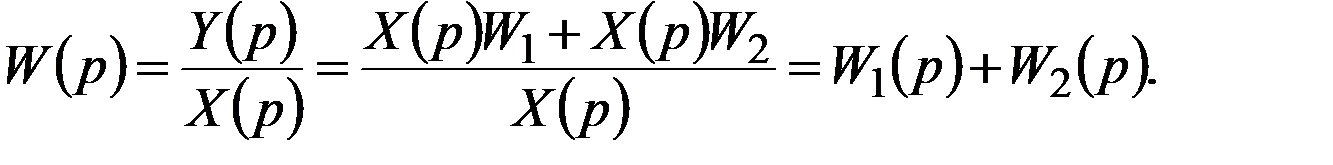
Передаточная функция цепи с обратной связью (рис. 1.15) равна:
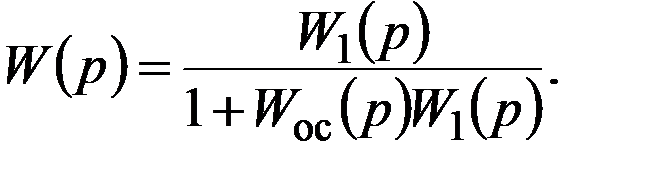
Если
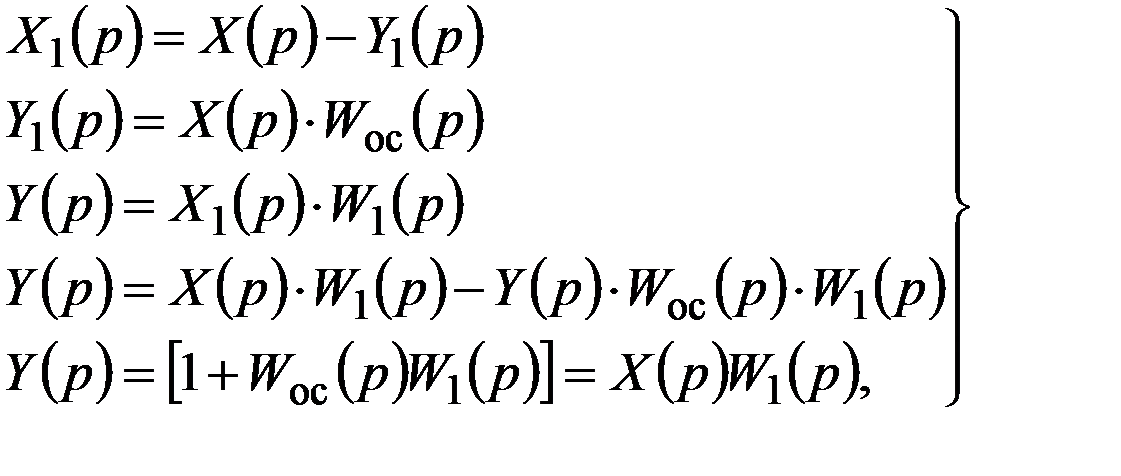
то
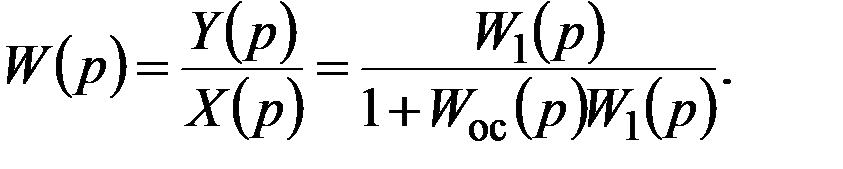
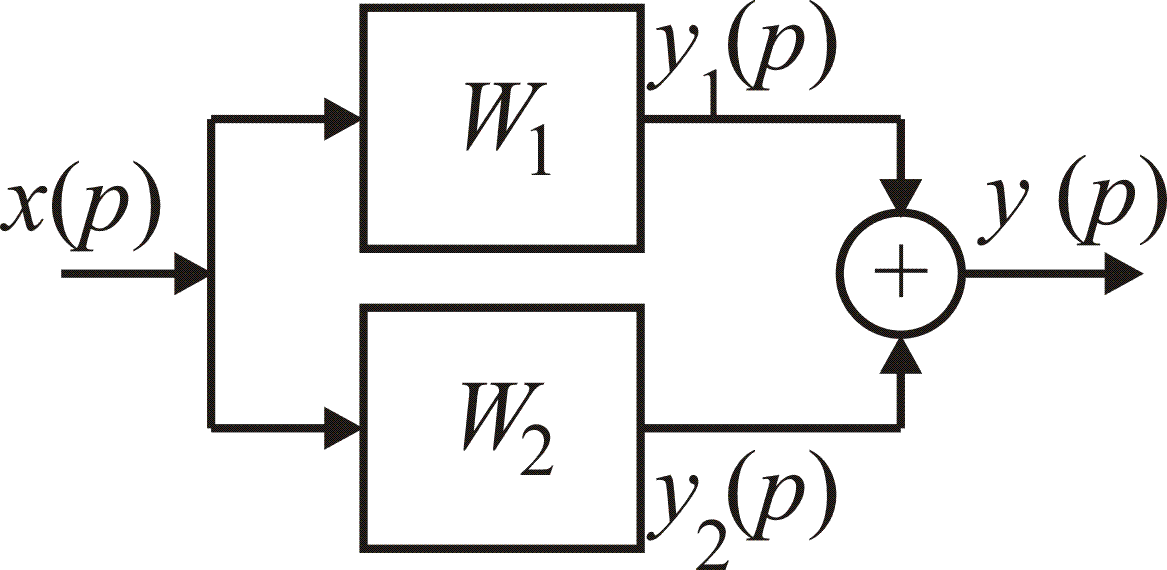
Рис. 1.14. Схема параллельного соединения типовых звеньев
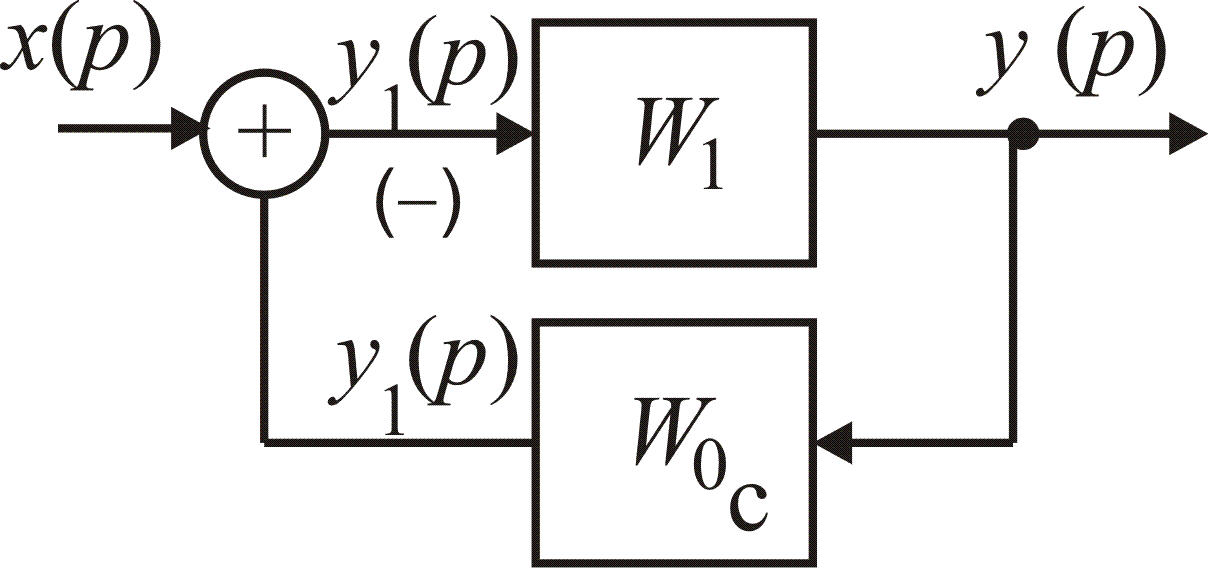
Рис. 1.15. Схема типового звена с обратной связью
Контрольные вопросы
1. Что представляет собой звено САР?
2. Напишите уравнение, отражающее математическую модель линейной САР (линейного звена) и объясните смысл переменных и коэффициентов этого уравнения.
3. Почему возникла необходимость применения оператора Лапласа?
4. Как определяют показатели переходного процесса в САР?
5. Какие характеристики линейного звена используются для количественного описания его свойств?
6.Назовите типовые звенья САР.
7. Как строится структурная схема САР?
8. Как определяется передаточная функция САР?
Понятие о качестве САР
Режимы работы САР
Практически все автоматические системы имеют два основных режима работы – переходный и установившийся. Отсюда – две математические модели функционирования одной и той же системы: динамическая, описывающая переходный процесс, и статическая – для описания установившегося режима.
Переходный режим является динамическим режимом работы системы, поэтому уравнения, описывающие его, называются уравнениями динамики и в большинстве случаев представляют собой систему дифференциальных уравнений. По физическому смыслу эти уравнения определяют движение системы (изменение состояния ОУ) при изменении управляющих и возмущающих воздействий.
По окончании переходного процесса система автоматики переходит в установившийся режим работы. Уравнения, описывающие этот этап работы САР, называются уравнениями статики и представляют собой, как правило, обычную систему алгебраических уравнений. В физическом смысле установившийся режим работы САР является предельным, равновесным состоянием, к которому стремится устойчивая система после окончания переходного режима.
Уравнения динамики носят более общий характер, нежели уравнения статики. Они содержат информацию как о вынужденной составляющей движения системы, вызванной внешним воздействием, так и о свободном движении (переходном процессе), обусловленном свойствами самой системы. Кроме того, зачастую из анализа уравнений динамики можно получить и систему уравнений статики.
Пусть, например, уравнение динамики САР представляет собой обычное дифференциальное уравнение n-го порядка:
(*)
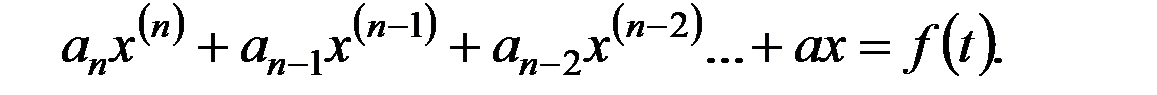Из курса высшей математики известно, что это уравнение описывает вынужденное движение системы при внешнем воздействии f(t). При этом левая часть уравнения характеризует переходный процесс или так называемые свободные колебания системы после окончания внешнего воздействия, т.е. когда воздействиеf(t) станет равным нулю.
Переходный режим любой САР и в физическом и в математическом смысле полностью описывается следующими тремя характеристиками:
- передаточной функцией;
- временной характеристикой;
- частотной характеристикой.
Каждая из этих характеристик по-своему, т.е. в своей области, отвечает на один и тот же вопрос: какова реакция данной САР на внешнее воздействие. Так, передаточная функция, описывая внутреннюю структуру системы, по сути, определяет преобразование сигнала внутри системы на его пути от входа к выходу (определяет алгоритм формирования выходного сигнала в системе с данной структурой). Временная характеристика дает представление о характере изменения переходного процесса в системе во времени, если на ее вход подан единичный внешний сигнал, т.е. описывает во времени реакцию системы на этот сигнал, т. е. дает представление о длительности реакции системы на это воздействие и изменения выходного сигнала во времени. А частотная характеристика определяет реакцию системы автоматики на весь спектр возможных внешних воздействий, что наиболее удобно рассматривать именно в частотной области.
Любая часть системы автоматического управления может быть рассмотрена как некоторое звено этой системы, преобразующее сигнал входа в сигнал выхода. Если в качестве такого звена рассматривается объект регулирования, то входными сигналами являются управляющие воздействия и внешние возмущения, а выходными – регулируемые величины.
Показатели переходного процесса в системах автоматического регулирования (САР) обычно определяют из анализа реакции системы на типовые внешние воздействия: гармонический сигнал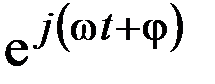 
или sin(ωt+φ), единичный скачок 1(t) и единичная импульсная функция δ(t) (дельта функция).
Дата: 2018-12-21, просмотров: 316.
