Предельные отклонения, не указанные непосредственно после номинальных размеров, а оговоренные общей записью в технических требованиях чертежа, называются неуказанными предельными отклонениями. Неуказанными могут быть только предельные отклонения относительно низкой точности. Числовые значения неуказанных предельных отклонений линейных размеров (кроме радиусов закругления и фасок) могут назначаться на основе ряда допусков, установленных двумя способами:
1) По квалитетам СТ СЭВ 145-75 и СТ СЭВ 177-75
2) По классам точности СТ СЭВ 302-76
Сочетания в одной общей записи неуказанных предельных отклонений для размеров различных элементов должны соответствовать одному из четырех вариантов согласно ГОСТ 25670-83:
1) H 14; h 14; 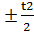 или H 14; h 14;
или H 14; h 14; 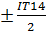
2) + t 2 ; - t 2 ; 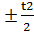
3) 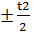 или
или 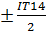 ;
;
4) 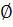 H 14;
H 14; 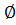 h 14;
h 14; 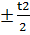 или
или 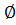 H 14;
H 14; 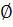 h 14;
h 14; 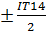
Примечания:
1) Допускается записи о неуказанных предельных отклонениях размеров дополнять поясняющими словами, например: «Неуказанные предельные отклонения размеров: H14; h14; 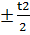 »
»
2) Если технические требования на чертеже состоят из одного пункта, содержащего запись о неуказанных предельных отклонениях размеров, или эта запись приводится в текстовых документах, то она должна обязательно сопровождаться поясняющими словами, например: «  »
»
1) Обозначения односторонних предельных отклонений по квалитетам, назначаемым только для круглых отверстий и валов (по ГОСТ 25670-83) дополняются знаком 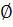 .
.
2) Если все предельные отклонения линейных размеров, указаны непосредственно после номинальных размеров, кроме радиусов и общая запись отсутствует, то неуказанные предельные отклонения радиусов закругления, фасок и углов должны соответствовать приведенным в ГОСТ25670-83 для квалитетов от 12 до 16 и на чертеже не оговариваются.
Примеры общих записей:
Неуказанные предельные отклонения размеров отверстий (охватывающих) – по А7,(охватываемых ) – по В7,остальных по СМ7.
Неуказанные предельные отклонения размеров диаметров по А5, В5, остальных по СМ7.
Шероховатость.
Под шероховатостью поверхностей понимается – совокупность микронеровностей с относительно малыми шагами. Всего 14 классов шероховатости. 1кл.- самый грубый. Высота микронеровностей измеряется в микронах (мкм.). 1мкм=0.001мм.
- способ обработки конструктором не устанавливается.
- поверхность образована только удалением слоя материала.
- поверхность образована без удаления слоя материала (литье, штамповка).
Основные параметры по которым оценивается шероховатость.
Ra – среднеарифметическая высота микронеровностей на базовой длине.
Rz – высота микронеровностей по 10 наибольшим выступам на базовой длине.
Rmax - наибольшая высота микронеровностей на базовой длине.
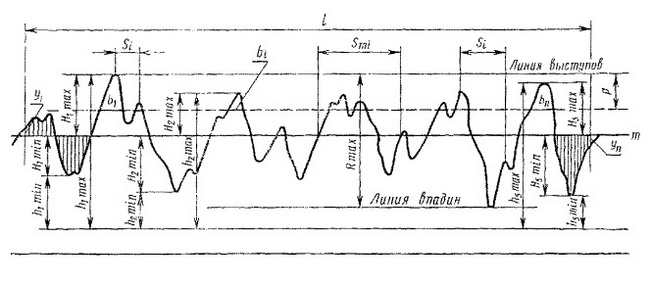
ГОСТ 2789-73г. изменение от 28.05.2002г.
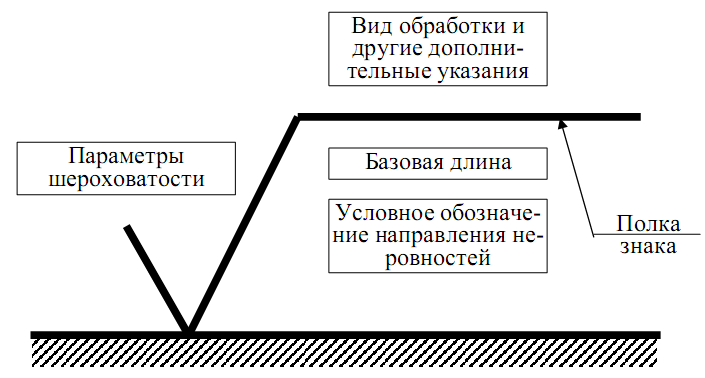
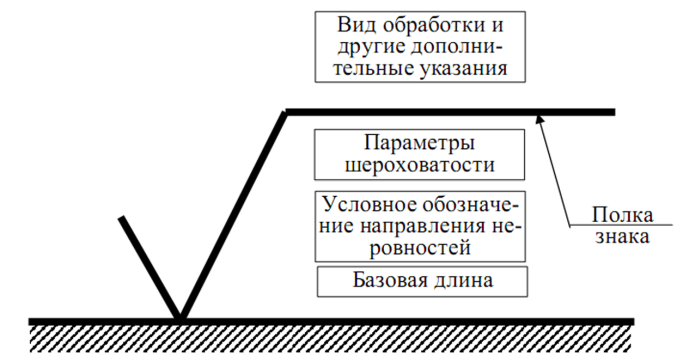
Обозначения шероховатости на чертежах по ГОСТ 2789-59г.-79г.- 2002г.
| ГОСТ 2789-59г. | ГОСТ 2789-73 г. | Изменение от 28.05.2002г. |
| |
| Класс шероховатости | Ra | Rz | Rmax | |
| ГОСТ 2789-59 | 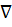 6 6
| (1.25-2.5) | (6.3- 10) | (6.3- 10) |
| ГОСТ 2789-73 | 2.0 | Rz7.0 | Rmaх7.0 | |
| Изменение от 28.05.2002г | Ra 2.0 | Rz 7.0 | Rmax 7.0 |
Если шероховатость обозначена 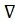 6, то величина микронеровностей - Ra может колебаться в пределах (1.25 - 2.5), Rz, Rmax – в пределах (6.3 -10).Если шероховатость обозначена Ra 2.0, то величина микронеровностей не более 2.0мкм, если Rz 7.0 и Rmax 7.0, то величина микронеровностей не более 7.0 мкм. В тех случаях, когда требуется ограничить максимальную и минимальную величины шероховатости указывают две величины R
6, то величина микронеровностей - Ra может колебаться в пределах (1.25 - 2.5), Rz, Rmax – в пределах (6.3 -10).Если шероховатость обозначена Ra 2.0, то величина микронеровностей не более 2.0мкм, если Rz 7.0 и Rmax 7.0, то величина микронеровностей не более 7.0 мкм. В тех случаях, когда требуется ограничить максимальную и минимальную величины шероховатости указывают две величины R 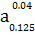 или Rz 7.0
или Rz 7.0 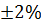 .
.
| Класс шероховатости | Ra, мкм | Ra, мкм | Rz, мкм |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  1 1
| 50 | 40 – 80 | 160 -320 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  2 2
| 25 | 20 – 40 | 80 – 160 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  3 3
| 12.5 | 10 – 20 | 40 – 80 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  4 4
| 6.3 | 5.0 – 10 | 20 – 40 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 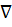 5 5
| 3.2 | 2.5 – 5.0 | 10 – 20 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 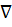 6 6
| 1.6 | 1.25 – 2.5 | 6.3 – 10 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 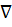 7 7
| 0.8 | 0.63 – 1.25 | 3.2 – 6.3 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 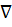 8 8
| 0.4 | 0.32 – 0.63 | 1.6 – 3.2 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  9 9
| 0.2 | 0.16 –0.32 | 0.8 – 1.6 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  10 10
| 0.1 | 0.08 – 0.16 | 0.4 – 0.8 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  11 11
| 0.05 | 0.04 – 0.08 | 0.2 – 0.4 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  12 12
| 0.025 | 0.02 – 0.04 | 0.1 – 0.2 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  13 13
| 0.012 | 0.01 – 0.02 | 0.05 – 0.1 |
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в?‡</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  14 14
| - | 0.008 – 0.01 | 0.032 – 0.05 |

Дата: 2018-12-21, просмотров: 766.