Для анализа непрерывных случайных величин применяется аппарат непрерывной математики. С определением функции распределения уже встречались в 2.1.

Функцией распределения случайной величины X называется функция F(x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньше x: .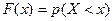

С помощью функции распределения можно дать строгое определение непрерывной СВ: Случайная величина называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек (является кусочно-диффернцируемой.)

Пример графика функции распределения для НСВ.

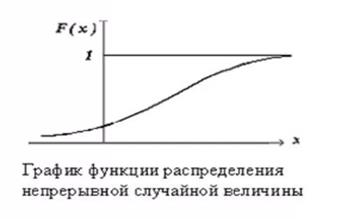
Согласно данному определению для НСВ график НСВ должен быть непрерывным, но возможно иметь точки излома (отсутствие дифференцируемости). Как будет показано далее, НСВ обладает свойствами, которыми не обладала ДСВ.

Напомним, что функция распределения для ДСВ кусочно-непрерывна .

Пример 1 .  НСВ  имеет функцию распределения.

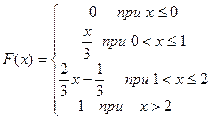
Так как эта функция непрерывна и кусочно-дифференцируема на множестве действительных чисел (вспомним определение непрерывности из курса высшей математики!), то СВ Х – непрерывна.

Теорема 1. Вероятность любого отдельно взятого значения непрерывной СВ равна нулю.

Доказательство: Оценим вероятность того, что НСВ Х примет значение, равное х₁. 

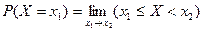. Применим свойство функции распределения:

Вероятность попадания случайной величины X в интервал 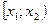 равна приращению ее функции распределения на этом интервале: 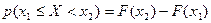. Получаем:

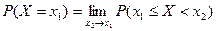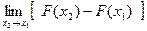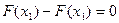= = . Использовали непрерывность функции распределения .

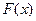Следствие. Если Х - непрерывная СВ, то вероятность попадания ее значений в интервал не зависит от того, является этот интервал открытым или закрытым.

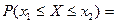
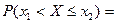
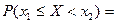
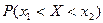
Рассмотрим вероятность попадания НСВ на участок  :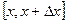

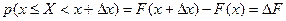- приращение функции распределения на этом участке.

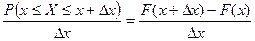Вероятность, приходящаяся на единицу длины, т.е. средняя плотность вероятности на участке  равна: . При предельном переходе при  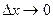получаем: 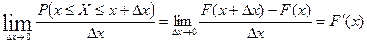(так как функция  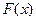дифференцируема).

Плотностью вероятности 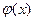 (плотностью распределения или просто плотнстью) НСВ Х называется производная ее функции распределения: .

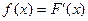Согласно определению: 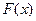 есть первообразная для .

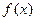Плотность вероятности, как и функция распределения является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных СВ. Если функцию распределения называют интегральной функцией (интегральным законом распределения), то плотность вероятности – дифференциальной функцией или дифференциальным законом распределения.

Пример 2 . Найти 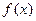для НСВ в ПР1 с функцией распределения

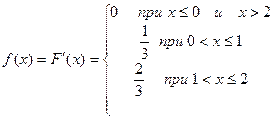
Определение. График плотности вероятности 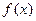  называют кривой распределения.