Раздел «Теория вероятностей и математическая статистика»
Тема 2 «СЛУЧАЙНЫЕ ВЕЛИЧИНЫ»
2.1. Случайные величины: виды, способы задания.
Функция распределения
Величину называют случайной, если в результате опыта она принимает лишь одно из возможных значений, заранее не известное и зависящее от случайных причин.
Примеры случайных величин:
1) число бракованных деталей в партии;
2) число студентов на данной лекции;
3) уровень воды в водоёме;
4) число выпавших очков при бросании игральной кости;
5) продолжительность сна студента в ночь перед экзаменом.
Случайная величина называется дискретной (ДСВ), если множество ее значений конечное или счетное.
Дискретная случайная величина принимает отдельные, изолированные друг от друга значения. В рассмотренных примерах 1,2,4 – дискретные случайные величины.
Случайная величина называется непрерывной (НСВ), если множество ее возможных значений является некоторым числовым промежутком. Примеры НСВ – 3,5.
Для работы со случайными величинами будем обозначать сами величины строчными буквами, а их возможные значения – прописными.
Случайную величину можно описать различными способами.
Наиболее полным описанием СВ является ее закон распределения.
Законом распределения СВ называется соответствие, устанавливающее связь между возможными значениями СВ и вероятностями их появления.
Для ДСВ закон распределения может быть дан в виде таблицы, аналитически (в виде формулы) и графически.
Табличное задание закона распределения ДСВ называют рядом распределения.
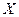
| 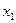
| 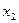
| … | 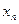
|
| P | 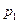
| 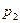
| … | 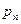
|
При этом 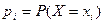 , так как события «Х примет значение
, так как события «Х примет значение 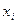 » образуют полную группу событий, то
» образуют полную группу событий, то 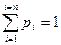 .
.
Таблица может быть и бесконечной, если множество значений ДСВ счетно. Но и в этом случае 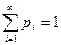 (ряд сходится и имеет сумму, равную 1).
(ряд сходится и имеет сумму, равную 1).
Пример 1. Вероятность попадания при одном выстреле по мишени равна 0,4. Найти вероятности возможного числа попадания в мишень, если было произведено 3 выстрела.
| Число попаданий | 0 | 1 | 2 | 3 |
| Вероятность | 0,216 | 0,432 | 0,288 | 0,064 |
Б) Аналитическое задание: указанные вероятности в предыдущем примере были найдены на основе формулы Бернулли при n=3 и p=0,4. Поэтому формула
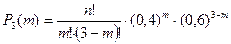 , определяет в аналитическом виде закон распределения вероятностей, где область определения m=0,1,2,3.,
, определяет в аналитическом виде закон распределения вероятностей, где область определения m=0,1,2,3.,
В) Графическое задание -. многоугольник распределения вероятностей – ломанная, вершины которой имеют координаты 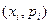 .
.
Функция распределения случайной величины. Ряд распределения, которым мы пользовались для описания дискретной случайной величины, не является единственным способом ее описания. Кроме того, он не применим для непрерывных СВ.
В ряде распределения указаны значения вероятностей событий p(X=xi )=pi .
Можно рассматривать вероятности других событий: p(X<xi ). Эта вероятность зависит от xi , т.е является функцией от xi
Функцией распределения случайной величины X называется функция F( x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньше x: 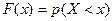 .
.
Функцию 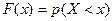 называют ещё интегральной функцией распределения.
называют ещё интегральной функцией распределения.
Пример 2.
| Xi | 0 | 2 | 4 |
| Pi | 0,2 | 0,6 | 0,2 |
1. Если 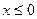 , то
, то 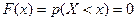
2. При 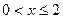 , то
, то 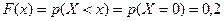
3. При 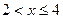 , то
, то 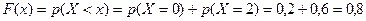 .
.
4. При 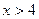 ,
,
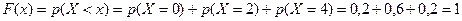 .
.
Получаем 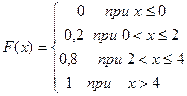
Свойства дисперсии .
Дисперсия D(X) случайной величины X определена следующим выражением: D(X)=M(X-M(X)) 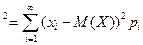 .
.
1. D ( X)= M( X2)-( M( X))2 . Данную формулу удобно использовать для вычислений дисперсии.
2. D(C )=0, где C=const;
3. D(CX)= 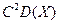 ;
;
4. D(X 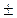 Y)=D(X)+D(Y), если X и Y – независимые случайные величины.
Y)=D(X)+D(Y), если X и Y – независимые случайные величины.
Дисперсия обладает неудобным свойством: её размерность равна размерности самой величины. Поэтому для оценки разброса значений Х используют ещё одну характеристику: среднее квадратическое отклонение (стандарт) СВ: 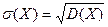 .
.
Среднеквадратичное отклонение имеет ту же размерность, что и сама случайная величина. Основной недостаток стандартного отклонения в том, что оно не обладает свойством аддитивности в отличие от дисперсии. Это означает, что, если для независимых случайных величин X и Y выполнимо свойство 4, то для стандартного отклонения :
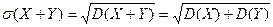 .
.
Числовые характеристики фиксируют свойства случайных величин, так как являются величинами постоянными, неслучайными.
Пример 1. Даны законы распределения двух независимых случайных величин:
| Х | 2 | 4 | 6 | 8 |
| Р | 0,4 | 0,2 | 0,1 | 0,3 |
| Y | 0 | 1 | 2 |
| Р | 0,5 | 0,2 | 0,3 |
Найти математическое ожидание случайной величины:Z = 2 X + 3 Y.
Решение: Из определения математического ожидания: 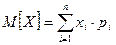
Используем следующие свойства математического ожидания:
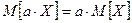 , где a – константа;
, где a – константа;
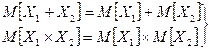 , где Х1, Х2 – независимые случайные величины.
, где Х1, Х2 – независимые случайные величины.
Тогда в нашем случае:
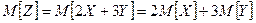
Вычислим математическое ожидание исходных случайных величин:
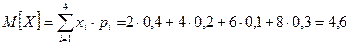
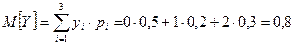
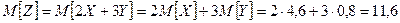
На практике, в качестве характеристик, дополняющих математическое ожидание, используют моду и медиану.
Модой Мо(Х) СВ Х называется ее наиболее вероятное значение (для которого вероятность или плотность вероятности достигает максимума.)
Если вероятность или плотность вероятности достигает максимума не в одной точке, то распределение – полимодальное.
Медианой Ме(Х) НСВ Х называется такое ее значение, для которого 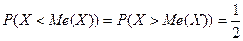 .
.
Геометрически прямая х=Ме(Х) проходит через такую точку, которая делит площадь фигуры под кривой распределения на две равные площади.
Квантилем уровня q СВ Х называется такое значение СВ , при котором значение ее функции распределения имеет значение , равное q, т.е. 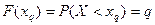 .
.
Квантиль уровня 0,5 есть медиана, т.е.Me(X)=x0,5
Выделяют еще нижний x0,25 и верхний x0,75 квантили.
Начальным моментом k-го порядка СВ Х называется математическое ожидание k-той степени этой величины : 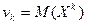 .
.
Центральным моментом k-го порядка СВ Х называется математическое ожидание k-той степени отклонения этой величины от ее математического ожидания : 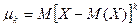 .
.
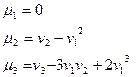 и т.д.
и т.д.
1) При k=1 первый начальный момент есть матожидание СВ. Характеризует среднее значение СВ или положение распределения СВ на числовой оси.
2) При k=2 второй центральный момент 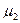 – дисперсия СВ. Степень рассеяния распределения относительно матожидания.
– дисперсия СВ. Степень рассеяния распределения относительно матожидания.
3) Третий центральный момент 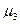 - характеризует скошенность распределения. Используется в коэффициенте асимметрии
- характеризует скошенность распределения. Используется в коэффициенте асимметрии 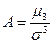 .
.
4) Четвертый центральный момент 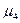 - характеризует крутость распределения. Используется для определения коэффициента эксцесса
- характеризует крутость распределения. Используется для определения коэффициента эксцесса 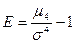 .
.
2.4. Типы распределения дискретных случайных величин
Показательное распределение
Определение Непрерывная случайная величина Х имеет показательный закон распределения с параметром 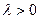 , если ее плотность вероятности
, если ее плотность вероятности 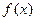 имеет вид
имеет вид
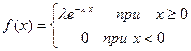 (1)
(1)
Кривая распределения 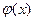 и график функции распределения имеют вид
и график функции распределения имеют вид
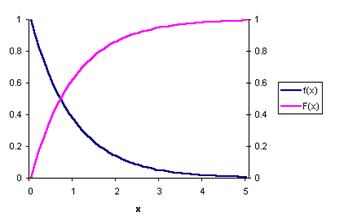
Получим выражение для функции распределения по формуле 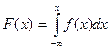 .
.
1) При 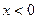
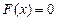 .
.
2) При 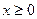
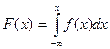
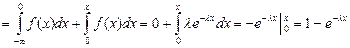 .
.
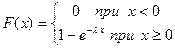
По соответствующим формулам получаем выражения для 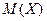 и
и 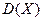 :
:
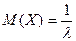 ;.
;. 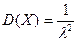
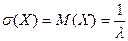
Пример Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.
Решение. Х- время безотказной работы прибора, среднее время- 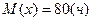 , тогда по формуле (3)
, тогда по формуле (3) 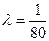 и по (1 )
и по (1 ) 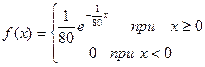 ; (2)
; (2) 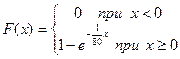 .
.
Искомая вероятность
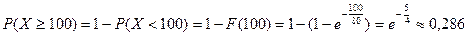 .
.
Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
Закон больших чисел
Известно, что нельзя заранее предвидеть, какое из возможных значений примет случайна величина (СВ) в результате опыта., но при некоторых условиях суммарное поведение большого числа СВ утрачивает случайный характер, а это значит, что возможно сформулировать некоторые закономерности в появлении СВ.
Знаний условий, при которых совокупное действие многих случайных причин приводит к предсказуемому результату очень важно для практики. Эти условия описываются теоремами, которые имеют общее название закона больших чисел.
Под законом больших чисел в широком смысле понимается общий принцип: совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. То есть при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности
2.8.1.Неравенство Маркова (лемма Чебышева)
Теорема Если СВ Х принимает только неотрицательные значения и имеет математическое ожидание 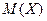 , то для любого положительного числа А верно неравенство
, то для любого положительного числа А верно неравенство
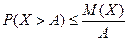 (НМ 1)- неравенство Маркова.
(НМ 1)- неравенство Маркова.
Неравенство Маркова можно записать и в другой форме. Так как события 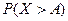 и
и 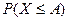 противоположны, то получаем
противоположны, то получаем 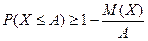 (НМ 2 )
(НМ 2 )
Отметим, что (1) и (2) в отличие от ранее рассмотренной интегральной теоремы Муавра – Лапласа дает лишь оценку (весьма грубую) для указанных вероятностей.
Неравенство Маркова применимо к любым неотрицательным СВ.
Пример 1. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделение банка будет обслужено: а) не более 200 клиентов; б) более 150 клиентов.
Решение. 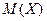 =100, а) А=200 и
=100, а) А=200 и 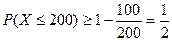 .
.
Ответ: вероятность не менее 0,5.
Б) А=150 и 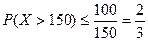 .
.
Ответ: вероятность не более 2/3.
Неравенство Чебышева
Одним из фактов, на которые опирается закон больших чисел, является неравенство Чебышева (НЧ), которое получается из неравенства Маркова применением его к СВ 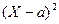 и так же имеет две эквивалентных формулировки.
и так же имеет две эквивалентных формулировки.
Теорема. (Неравенство Чебышева). Для любой СВ, имеющей математическое ожидание 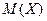 и дисперсию
и дисперсию 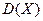 , справедливо неравенство
, справедливо неравенство
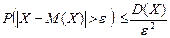 (НЧ 1) (
(НЧ 1) ( 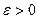 )
)
(вероятность того, что отклонение СВ Х от ее математического ожидания по абсолютной величине больше положительного числа 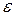 , не больше ,чем
, не больше ,чем 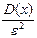 )
)
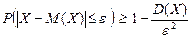 (НЧ 2)
(НЧ 2)
(вероятность того, что отклонение СВ Х от ее математического ожидания по абсолютной величине не больше положительного числа 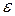 , не меньше ,чем
, не меньше ,чем 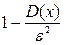 ).
).
НЧ имеет для практики ограниченное значение, т.к. дает грубую оценку, хотя устанавливает верхнюю и нижнюю границу вероятности рассматриваемого события.
Пример 2. Вероятность выхода с автомата стандартной детали равна 0,96. Оценить с помощью НЧ вероятность того, что число бракованных среди 2000 деталей находится в границах от 60 до 100 (включительно).
Решение. СВ Х – число бракованных деталей распределена биномиально. По условию вероятность бракованной детали р=1-0,96=0,04. Тогда 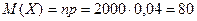 и
и 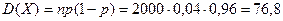 .
.
Оценка вероятности события
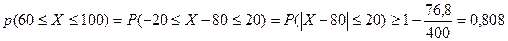 , т.к.
, т.к. 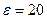 .
.
Т.е. по НЧ вероятность того, что число бракованных среди 2000 деталей находится в границах от 60 до 100 (включительно) не менее чем 0,808.
Сравним эту вероятность с той, которую для этого события можно найти по интегральной теореме Муавра- Лапласа
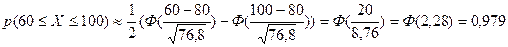 .
.
Полученное значение по Т Муавра –Лапласа не противоречит оценке, полученной по НЧ. Значение 0,979 более точное, так как оно получено в соответствии с учетом распределения этой СВ Х. Но зато НЧ дает оценку для любой СВ, не обязательно распределенной по биномиальному закону.
Результаты полученные по НМ и НЧ не всегда практически значимы, так как при 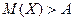 в НМ и при
в НМ и при 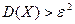 получаем очевидные результаты.
получаем очевидные результаты.
Теорема Чебышева
Теорема Чебышева. Если СВ Х1, Х2,…,Х n,… - попарно независимы и их дисперсии равномерно ограничены (не превышают постоянного числа С), то , как бы мало ни было положительное число 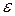 , вероятность неравенства
, вероятность неравенства
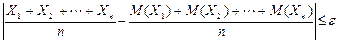
будет как угодно близка к единице, если число случайных величин достаточно велико.
ИЛИ с использованием предельного перехода
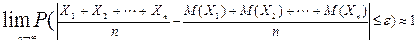
(средняя арифметическая СВ сходится по вероятности к средней арифметической их матожиданий).
Сущность теоремы: хотя отдельные независимые СВ могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа СВ с большой вероятностью принимает значения , близкие к определенному постоянному числу (среднее арифметическое математических ожиданий). То есть отдельные СВ могут иметь значительный разброс, а их среднее арифметическое рассеяно мало.
Среднее арифметическое достаточно большого число независимых СВ (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Причина: отклонения каждой СВ от своих МО могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.
Из неравенства (*) в формулировке ТЧ получим еще одно удобную оценку.
По условию дисперсии СВ равномерно ограничены. Например, числом С.
Пусть 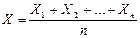 - СВ «среднее матожидание». Тогда
- СВ «среднее матожидание». Тогда 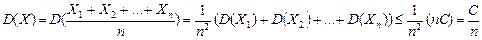 . Для СВ Х применим Н Чебышева
. Для СВ Х применим Н Чебышева 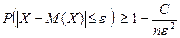 , где
, где 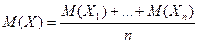 .
.
Замечание НЧ можно записать и так : 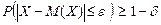 , где
, где 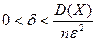
Пример 3. Сколько надо провести измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 1 (по абсолютной величине) , если среднее квадратическое отклонение каждого измерения не превосходит 5? )(Кремер, с. 234)
Решение. Хi – результат i- того измерения.; а- истинное значение величины.. т.е. при любом измерении M(Xi)=a, 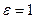 , с=52=25 . Нужно найти число измерений n, при котором
, с=52=25 . Нужно найти число измерений n, при котором 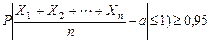 . Данное неравенство будет выполняться, если
. Данное неравенство будет выполняться, если 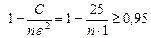 . Откуда
. Откуда 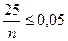 и
и 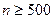 .
.
Ответ: потребуется не менее 500 измерений.
На ТЧ основан широко применяемый в статистике выборочный метод: по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов.
Теорема Бернулли
Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико, т.е. имеет место равенство
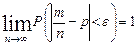 .
.
Замечние. Теорему Бернулли (ТБ) можно записать и так: 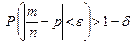 , где
, где 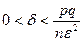 и q=1- p.
и q=1- p.
ТБ была доказана ранее ТЧ, но непосредственно из нее следует, так как частоту (частность) события можно представить как среднюю арифметическую независимых альтернативных СВ. Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости.
ТБ позволяет заменить теоретическую неизвестную вероятность частотой наступления события, которая может быть получена из опыта. Теорема Бернулли получила название «закона больших чисел» и положила начало теории вероятностей как науке.
Обобщением ТБ является Теорема Пуассона. Она рассматривает случай, когда в каждом испытании вероятности наступления события могут оказаться различными 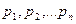 .
.
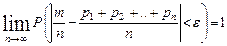 .
.
Вывод. Теоремы, имеющие общее название «закон больших чисел» устанавливают факт приближения большого числа СВ к определенным постоянным. Но этим не ограничиваются закономерности, возникающие в результате суммарного воздействия СВ. При некоторых условиях совокупное действие СВ приводит к нормальному закону распределения. Описанием этих условий посвящены теоремы под общим названием «центральная предельная теорема».
В современных центральных предельных теоремах в качестве предельных распределений рассматриваются распределения, отличные от нормального, обычно это локальные предельные теоремы (распределение Пуассона, Коши распределения, распределение Стьюдента, c2 – распределение и др).
Раздел «Теория вероятностей и математическая статистика»
Тема 2 «СЛУЧАЙНЫЕ ВЕЛИЧИНЫ»
2.1. Случайные величины: виды, способы задания.
Функция распределения
Величину называют случайной, если в результате опыта она принимает лишь одно из возможных значений, заранее не известное и зависящее от случайных причин.
Примеры случайных величин:
1) число бракованных деталей в партии;
2) число студентов на данной лекции;
3) уровень воды в водоёме;
4) число выпавших очков при бросании игральной кости;
5) продолжительность сна студента в ночь перед экзаменом.
Случайная величина называется дискретной (ДСВ), если множество ее значений конечное или счетное.
Дискретная случайная величина принимает отдельные, изолированные друг от друга значения. В рассмотренных примерах 1,2,4 – дискретные случайные величины.
Случайная величина называется непрерывной (НСВ), если множество ее возможных значений является некоторым числовым промежутком. Примеры НСВ – 3,5.
Для работы со случайными величинами будем обозначать сами величины строчными буквами, а их возможные значения – прописными.
Случайную величину можно описать различными способами.
Наиболее полным описанием СВ является ее закон распределения.
Законом распределения СВ называется соответствие, устанавливающее связь между возможными значениями СВ и вероятностями их появления.
Для ДСВ закон распределения может быть дан в виде таблицы, аналитически (в виде формулы) и графически.
Табличное задание закона распределения ДСВ называют рядом распределения.
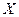
| 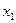
| 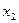
| … | 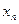
|
| P | 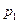
| 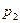
| … | 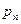
|
При этом 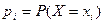 , так как события «Х примет значение
, так как события «Х примет значение 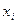 » образуют полную группу событий, то
» образуют полную группу событий, то 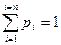 .
.
Таблица может быть и бесконечной, если множество значений ДСВ счетно. Но и в этом случае 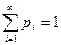 (ряд сходится и имеет сумму, равную 1).
(ряд сходится и имеет сумму, равную 1).
Пример 1. Вероятность попадания при одном выстреле по мишени равна 0,4. Найти вероятности возможного числа попадания в мишень, если было произведено 3 выстрела.
| Число попаданий | 0 | 1 | 2 | 3 |
| Вероятность | 0,216 | 0,432 | 0,288 | 0,064 |
Б) Аналитическое задание: указанные вероятности в предыдущем примере были найдены на основе формулы Бернулли при n=3 и p=0,4. Поэтому формула
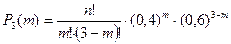 , определяет в аналитическом виде закон распределения вероятностей, где область определения m=0,1,2,3.,
, определяет в аналитическом виде закон распределения вероятностей, где область определения m=0,1,2,3.,
В) Графическое задание -. многоугольник распределения вероятностей – ломанная, вершины которой имеют координаты 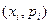 .
.
Функция распределения случайной величины. Ряд распределения, которым мы пользовались для описания дискретной случайной величины, не является единственным способом ее описания. Кроме того, он не применим для непрерывных СВ.
В ряде распределения указаны значения вероятностей событий p(X=xi )=pi .
Можно рассматривать вероятности других событий: p(X<xi ). Эта вероятность зависит от xi , т.е является функцией от xi
Функцией распределения случайной величины X называется функция F( x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньше x: 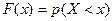 .
.
Функцию 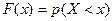 называют ещё интегральной функцией распределения.
называют ещё интегральной функцией распределения.
Пример 2.
| Xi | 0 | 2 | 4 |
| Pi | 0,2 | 0,6 | 0,2 |
1. Если 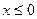 , то
, то 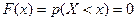
2. При 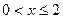 , то
, то 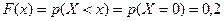
3. При 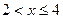 , то
, то 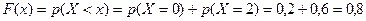 .
.
4. При 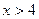 ,
,
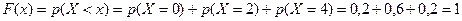 .
.
Получаем 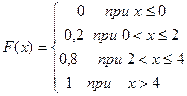
Дата: 2018-12-21, просмотров: 387.