Как было показано выше, случайная величина полностью определяется своей функцией распределения или законом распределения. В некоторых случаях бывает достаточно проанализировать часть свойств случайной величины, которые фиксируются в специальных числовых характеристиках, знание которых поможет получить информацию о случайной величине.
Математическое ожидание М(Х) дискретной случайной величины X определяется следующим образом: 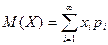 .
.
Из этого определения следует, что математическое ожидание есть некоторая постоянная величина. Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно (в особенности для большого числа испытаний) среднему арифметическому значению СВ.
Разность между СВ и ее математическим ожиданием называют отклонением X от M(X)
Свойства математического ожидания:
1. М(С)=С, где С-const;
2. M(CX)=CM(X);
3. M(X 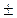 Y)=M(X)
Y)=M(X) 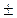 M(Y), где X,Y–любые случайные величины;
M(Y), где X,Y–любые случайные величины;
4. M(XY)=M(X)M(Y), если X и Y – независимые случайные величины.
5. M[X- M( X)]=0 (математическое отклонение величины от ее математического ожидания равна 0.)
Дисперсия(рассеяние) D(X) случайной величины X определена следующим выражением: D(X)=M(X-M(X)) 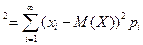 и характеризует меру разброса значений СВ вокруг математического ожидания этой СВ.
и характеризует меру разброса значений СВ вокруг математического ожидания этой СВ.
Чем больше дисперсия, тем более «случайной» является СВ.
Свойства дисперсии .
Дисперсия D(X) случайной величины X определена следующим выражением: D(X)=M(X-M(X)) 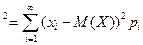 .
.
1. D ( X)= M( X2)-( M( X))2 . Данную формулу удобно использовать для вычислений дисперсии.
2. D(C )=0, где C=const;
3. D(CX)= 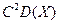 ;
;
4. D(X 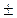 Y)=D(X)+D(Y), если X и Y – независимые случайные величины.
Y)=D(X)+D(Y), если X и Y – независимые случайные величины.
Дисперсия обладает неудобным свойством: её размерность равна размерности самой величины. Поэтому для оценки разброса значений Х используют ещё одну характеристику: среднее квадратическое отклонение (стандарт) СВ: 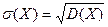 .
.
Среднеквадратичное отклонение имеет ту же размерность, что и сама случайная величина. Основной недостаток стандартного отклонения в том, что оно не обладает свойством аддитивности в отличие от дисперсии. Это означает, что, если для независимых случайных величин X и Y выполнимо свойство 4, то для стандартного отклонения :
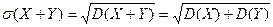 .
.
Числовые характеристики фиксируют свойства случайных величин, так как являются величинами постоянными, неслучайными.
Пример 1. Даны законы распределения двух независимых случайных величин:
| Х | 2 | 4 | 6 | 8 |
| Р | 0,4 | 0,2 | 0,1 | 0,3 |
| Y | 0 | 1 | 2 |
| Р | 0,5 | 0,2 | 0,3 |
Найти математическое ожидание случайной величины:Z = 2 X + 3 Y.
Решение: Из определения математического ожидания: 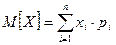
Используем следующие свойства математического ожидания:
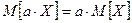 , где a – константа;
, где a – константа;
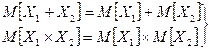 , где Х1, Х2 – независимые случайные величины.
, где Х1, Х2 – независимые случайные величины.
Тогда в нашем случае:
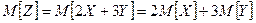
Вычислим математическое ожидание исходных случайных величин:
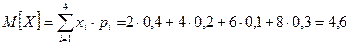
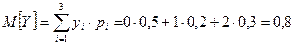
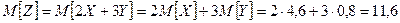
На практике, в качестве характеристик, дополняющих математическое ожидание, используют моду и медиану.
Модой Мо(Х) СВ Х называется ее наиболее вероятное значение (для которого вероятность или плотность вероятности достигает максимума.)
Если вероятность или плотность вероятности достигает максимума не в одной точке, то распределение – полимодальное.
Медианой Ме(Х) НСВ Х называется такое ее значение, для которого 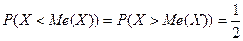 .
.
Геометрически прямая х=Ме(Х) проходит через такую точку, которая делит площадь фигуры под кривой распределения на две равные площади.
Квантилем уровня q СВ Х называется такое значение СВ , при котором значение ее функции распределения имеет значение , равное q, т.е. 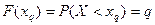 .
.
Квантиль уровня 0,5 есть медиана, т.е.Me(X)=x0,5
Выделяют еще нижний x0,25 и верхний x0,75 квантили.
Начальным моментом k-го порядка СВ Х называется математическое ожидание k-той степени этой величины : 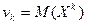 .
.
Центральным моментом k-го порядка СВ Х называется математическое ожидание k-той степени отклонения этой величины от ее математического ожидания : 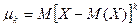 .
.
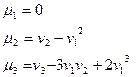 и т.д.
и т.д.
1) При k=1 первый начальный момент есть матожидание СВ. Характеризует среднее значение СВ или положение распределения СВ на числовой оси.
2) При k=2 второй центральный момент 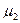 – дисперсия СВ. Степень рассеяния распределения относительно матожидания.
– дисперсия СВ. Степень рассеяния распределения относительно матожидания.
3) Третий центральный момент 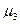 - характеризует скошенность распределения. Используется в коэффициенте асимметрии
- характеризует скошенность распределения. Используется в коэффициенте асимметрии 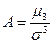 .
.
4) Четвертый центральный момент 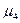 - характеризует крутость распределения. Используется для определения коэффициента эксцесса
- характеризует крутость распределения. Используется для определения коэффициента эксцесса 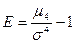 .
.
2.4. Типы распределения дискретных случайных величин
Дата: 2018-12-21, просмотров: 345.