Пусть твердое тело под действием внешних сил вращается во­круг оси Oz с угловой скоростью ω (рис. 17.3).

Рассматривая твердое тело как механическую систему, разо­бьем ее на множество материальных точек с массами Δmk. Каждая точка движется по окружности радиуса rk с касательным ускорени­ем a^t_k = ε r k и нормальным ускорением aⁿ_k = ω² r k , где ε — угловое ускорение.

Используем для каждой точки принцип Даламбера и приложим силы инерции:

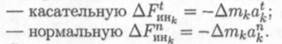
Система сил, действующих на точку, по принципу Даламбера, находится в равновесии.

Поэтому алгебраическая сумма моментов относительно оси вра­щения должна быть равна нулю:

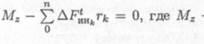               момент внешних сил.

Моменты нормальных сил инерции F"_инk равны нулю, т. к. силы пересекают ось z .  Силы,   направленные   по   касательной  к   окружно­сти,   равны

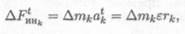
             Тема 1.15. Общие теоремы динамики                               125

где ε — общая величина, угловое ускорение тела.

Подставив значение силы в формулу для определения моментов, получим

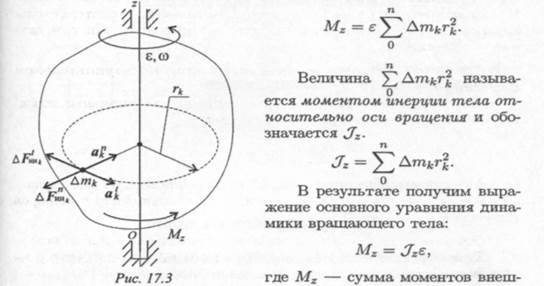
них сил относительно оси; ε — угловое ускорение тела.

Момент инерции тела в этом выражении определяет меру инертности тела при вращении.

По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ [J z] = [mr²] =кг∙м².

Видно, что значение момента инерции зависит от распределения массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от оси вращения. Для увеличения момента инерции используют колеса со спицами и отверстиями.

Моменты    инерции    некоторых   тел

126                                                  Лекция 17

Примеры решения задач

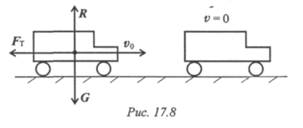
Пример 1. Автомобиль двигался со скоростью 54 км/ч. В ре­зультате резкого торможения автомобиль остановился. Определите время торможения, если коэффициент трения между поверхностью дороги и колесами автомобиля 0,36.

Решение

Принимаем автомобиль за материальную точку (рис. 17.8).

1. Считаем, что торможение произошло только за счет трения.
Используем   теорему  об  изменении  количества  движения.  Начальная  скорость

     54∙1000

vo = ——— = 15 м/с. По теореме изменения количества движения mv — mvo = F_Tt .

         3600

 Конечная скорость v = 0 (остановка).

2. Тормозная сила F_T = — fR .  

                                                    R = G = т q ,

здесь R — сила прижатия; f— коэффициент трения; G — сила тяжести; т — масса автомобиля; q — ускорение свободного падения; q = 9,81м/с².

                  Тема 1.15. Общие теоремы динамики                                 127

3.  После  подстановок   получаем   формулу  для  определения   вре­мени торможения.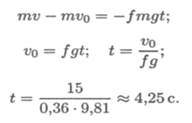                 

Пример 2. После отключения двигателя колесо радиусом 0,5 м и массой 700 кг имело угловую частоту вра­щения 300 об/мин. Определите момент трения в подшипниках, если вал колеса остановился через 1,5 мин. Вращение принять равнопере­менным, колесо считать сплошным цилиндром (рис. 17.9).       

                                              Решение

1. Запишем уравнение динамики при вращении:

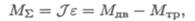
где M∑ — суммарный момент внешних сил; J — момент инерции; ε — угловое ускорение; М_дв — движущий момент; М_тр — момент трения (сил сопротивления).

2. Определим угловое ускорение по формуле для угловой скорости при равно-переменном движении:

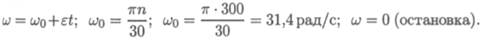
128                                                                         Лекция 17

   Тогда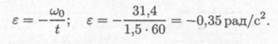           

3. Определим момент инерции колеса, считая его сплошным цилиндром:                                            

4. Определяем величину тормозного момента — момента трения
в подшипниках: М_дв = 0; —М_тр = Jε ;

-М_тр = 87,5(-0,35); М_тр = 30,625 Н∙м.

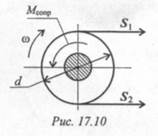
Пример 3. Шкив приводится во вращение ременной передачей (рис. 17.10). Натяжение ведущей ветви ремня S 1 = 120 Н, ведомой — S 2 = 50 Н. Масса шкива 200 кг, диаметр 80 мм, момент сопроти­вления в подшипниках 1,2 Н∙м. Определить угловое ускорение вала, пренебрегая его массой. Шкив считать тонкостенным цилиндром.

                      Решение

1. Используем основное уравнение ди­намики M∑ = J ε .

2. Определяем суммарный момент внешних cил                                            

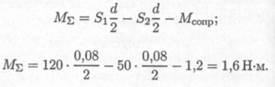
3. Рассчитываем момент инерции шкива, влиянием вала пренебрегаем:

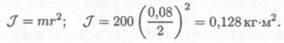
4. Определяем угловое    ускорение    шкива

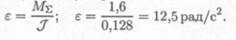
                Тема 1.15. Общие теоремы динамики                                 129

               Контрольные  вопросы  и  задания

1. Тело массой 10 кг поднято на высоту 6 м. Определите потенциальную энергию тела и работу, которую совершит тело при падении с этой высоты.

2. Материальная точка массой 16 кг, движущаяся со скоростью 10 м/с, остановилась через 40 с. Определите величину тормозной силы.

3. Тело массой 9,2 кг двигалось из состояния покоя 3с с ускорением 4 м/с² под действием силы F . Определите запас кинетической энергии, накопленный телом.

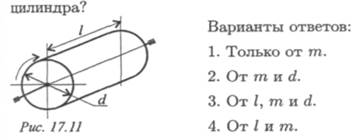
4. Сплошной однородный цилиндр вращается вокруг продольной оси (рис. 17.11). От каких параметров зависит момент инерции

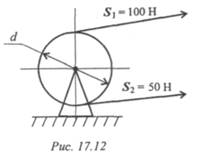
5. Определите вращающий момент на шкиве (рис. 17.12); d = 60 мм.

6. По результату решения предыдущей задачи (вопрос 5) определите момент инерции шкива, если, двигаясь из состояния покоя, он приобрел угловую скорость 50 рад/с за 10 с.

Примечание. При ответах на контрольные во­просы ускорение свободного па­дения можно принимать равным 10 м/с².

5 - 8060 Олофинская

130                                         Практическое занятие 1                   

  ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО РАЗДЕЛУ

«Теоретическая механика»

Практическое занятие 1