Прочность — способность не разрушаться под нагрузкой. Жесткость — особность незначительно деформироваться под нагрузкой.
Тема 2.1. Основные положения 163
Выносливость — способность длительное время выдерживать переменные нагрузки.
Устойчивость — способность сохранять первоначальную форму упругого равновесия.
Вязкость — способность воспринимать ударные нагрузки.
Виды расчетов
Расчет на прочность обеспечивает неразрушение конструкции.
Расчет на жесткость обеспечивает деформации конструкции под нагрузкой в пределах допустимых норм.
Расчет на выносливость обеспечивает необходимую долговечность элементов конструкции.
Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.
Для обеспечения прочности конструкций, работающих при ударных нагрузках (при ковке, штамповке и подобных случаях), проводятся расчеты на удар.
Основные гипотезы и допущения
Приступая к расчетам конструкции, следует решить, что в данном случае существенно, а что можно отбросить, т. к. решение технической задачи с полным учетом всех свойств реального объекта невозможно.
Допущения о свойствах материалов
Материалы однородные — в любой точке материалы имеют одинаковые физико-механические свойства.
Материалы представляют сплошную среду — кристаллическое строение и микроскопические дефекты не учитываются.
Материалы изотропны — механические свойства не зависят от направления нагружения.
Материалы обладают идеальной упругостью — полностью восстанавливают форму и размеры после снятия нагрузки.
В реальных материалах эти допущения выполняются лишь отчасти, но принятие таких допущений упрощает расчет. Все упрощения принято компенсировать, введя запас прочности.
164 Лекция 18
Допущения о характере деформации
Все материалы под нагрузкой деформируются, т. е. меняют форму и размеры.
Характер деформации легко проследить при испытании материалов на растяжение.
Перед испытаниями цилиндрический образец закрепляется в захватах разрывной машины, растягивается и доводится до разрушения. При этом записывается зависимость между приложенным усилием и деформацией. Получают график, называемый диаграммой растяжения. Для примера на рис. 18.1 представлена диаграмма растяжения малоуглеродистой стали.
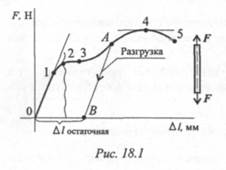На диаграмме отмечают особые точки:
— от точки 0 до точки 1 — прямая линия (деформация прямо пропорциональна нагрузке);
— от точки 2 до точки 5 деформации быстро нарастают и образец разрушается, разрушению предшествует появление утончения (шейки) в точке 4.
Если прервать испытания до точки 2, образец вернется к исходным размерам; эта область называется областью упругих деформаций. Упругие деформации полностью исчезают после снятия нагрузки.
При продолжении испытаний после точки 2 образец уже не возвращается к исходным размерам, деформации начинают накапливаться.
При выключении машины в точке А образец несколько сжимается по линии АВ, параллельной линии 01. Деформации после точки 2 называются пластическими, они полностью не исчезают; сохранившиеся деформации называются остаточными.
На участке 01 выполняется закон Гука:
В пределах упругости деформации прямо пропорциональны нагрузке.
Считают, что все материалы подчиняются закону Гука.
Поскольку упругие деформации малы по сравнению с геометрическими размерами детали , при расчетах считают , что размеры под
Тема 2.1. Основные положения 165
нагрузкой не изменяются.
Расчеты ведут, используя принцип начальных размеров. При работе конструкции деформации должны оставаться упругими.
К нарушению прочности следует относить и возникновение пластических деформаций. Хотя в практике бывают случаи, когда местные пластические деформации считаются допустимыми.
Классификация нагрузок и элементов конструкции
Классификация нагрузок
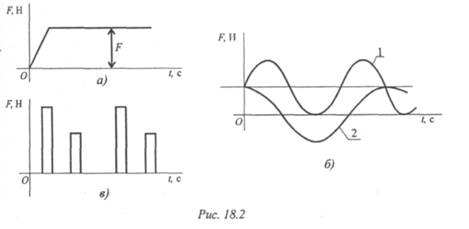
Статистические нагрузки (рис. 18.2а) не меняются со временем или меняются очень медленно. При действии статистических нагрузок проводится расчет на прочность.
Повторно-переменные нагрузки (рис. 18.26) многократно меняют значение или значение и знак. Действие таких нагрузок вызывает усталость металла.
Динамические нагрузки (рис. 18.2в) меняют свое значение в короткий промежуток времени, они вызывают большие ускорения и силы инерции и могут привести к внезапному разрушению конструкции.
Из теоретической механики известно, что по способу приложения нагрузки могут быть сосредоточенными или распределенными по поверхности.
166 Лекция 18
Реально передача нагрузки между деталями происходит не в точке, а на некоторой площадке, т.е. нагрузка является распределенной.
Однако если площадка контакта пренебрежительно мала по сравнению с размерами детали, силу считают сосредоточенной.
При расчетах реальных деформируемых тел в сопротивлении материалов заменять распределенную нагрузку сосредоточенной не следует.
Аксиомы теоретической механики в сопротивлении материалов используются ограниченно.
Нельзя переносить пару сил в другую точку детали, перемещать сосредоточенную силу вдоль линии действия, нельзя систему сил заменять равнодействующей при определении перемещений. Все вышеперечисленное меняет распределение внутренних сил в конструкции.
Формы элементов конструкции
Все многообразие форм сводится к трем видам по одному признаку.
1. Брус — любое тело, у которого длина значительно больше других размеров.
В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:
— прямой брус постоянного поперечного сечения (рис. 18.3а);
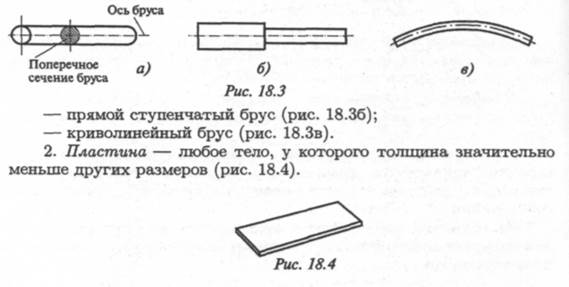
Тема 2.1. Основные положения 167
3. Массив — тело, у которого три размера одного порядка.
Контрольные вопросы и задания
1. Что называется прочностью, жесткостью, устойчивостью?
2. По какому принципу классифицируют нагрузки в сопротивлении материалов? К какому виду разрушений приводят повторно-переменные нагрузки?
3. Какие нагрузки принято считать сосредоточенными?
4. Какое тело называют брусом? Нарисуйте любой брус и укажите ось бруса и его поперечное сечение. Какие тела называют пластинами?
5. Что называется деформацией? Какие деформации называют упругими?
6. При каких деформациях выполняется закон Гука? Сформулируйте закон Гука.
7. Что такое принцип начальных размеров?
8. В чем заключается допущение о сплошном строении материалов? Поясните допущение об однородности и изотропности материалов.
168 Лекция 19
ЛЕКЦИЯ 19
Тема 2.1. Основные положения.
Нагрузки внешние и внутренние,
метод сечений
Знать метод сечений, внутренние силовые факторы, составляющие напряжений.
Уметь определять виды нагружений и внутренние силовые факторы в поперечных сечениях.
Элементы конструкции при работе испытывают внешнее воздействие, которое оценивается величиной внешней силы. К внешним силам относят активные силы и реакции опор.
Под действием внешних сил в детали возникают внутренние силы упругости, стремящиеся вернуть телу первоначальную форму и размеры.
Внешние силы должны быть определены методами теоретической механики, а внутренние определяются основным методом сопротивления материалов — методом сечений.
В сопротивлении материалов тела рассматриваются в равновесии. Для решения задач используют уравнения равновесия, полученные в теоретической механике для тела в пространстве.
Используется система координат, связанная с телом. Чаще продольную ось детали обозначают z , начало координат совмещают с левым краем и размещают в центре тяжести сечения.
Метод сечений
Метод сечений заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных частей.
Если все тело находится в равновесии, то и каждая его часть находится в равновесии под действием внешних и внутренних сил. Внутренние силы определяются из уравнений равновесия, составленных для рассматриваемой части тела.
Рассекаем тело поперек плоскостью (рис. 19.1). Рассматриваем правую часть. На нее действуют внешние силы F4 ; F5 ; F6 и внутренние силы
Тема 2.1. Основные положения 169
упругости q k , распределенные по сечению. Систему распределенных сил можно заменить главным вектором R q , помещенным в центр тяжести сечения, и суммарным моментом сил Mo:
n
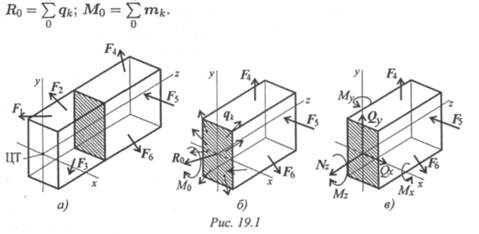
Разложив главный вектор Rо по осям, получим три составляющие:
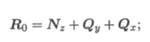
где Nz — продольная сила;
Qx — поперечная сила по оси х;
Qy — поперечная сила по оси у.
Главный момент тоже принято представлять в виде моментов пар сил в трех плоскостях проекции:
М0 = Мх + Му + М z ,
Мх — момент сил относительно Ох; Му — момент сил относительно Оу; Mz — момент сил относительно Oz .
Полученные составляющие сил упругости носят название внутренних силовых факторов. Каждый из внутренних силовых факторов вызывает определенную деформацию детали. Внутренние силовые факторы уравновешивают приложенные к этому элементу детали внешние силы. Используя шесть уравнений равновесия, можно получить величину внутренних силовых факторов:
170 Лекция 19
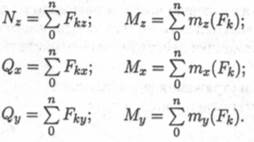
Из приведенных уравнений следует, что:
Nz — продольная сила, равная алгебраической сумме проекций на ось Oz внешних сил, действующих на отсеченную часть бруса; вызывает растяжение или сжатие;
Qx — поперечная сила, равная алгебраической сумме проекций на ось Qx внешних сил, действующих на отсеченную часть;
Qy — поперечная сила, равная алгебраической сумме проекций на ось Оу внешних сил, действующих на отсеченную часть;
силы Qx и Qy вызывают сдвиг сечения;
Мг — крутящийся момент, равный алгебраической сумме моментов внешних сил относительно продольной оси Oz ; вызывает скручивание бруса;
Мх — изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси Ох;
Му — изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси Оу;
моменты Мх и Му вызывают изгиб бруса в соответствующей плоскости.
Напряжения
Метод сечений позволяет определить величину внутреннего силового фактора в сечении, но не дает возможности установить закон распределения внутренних сил по сечению. Для оценки прочности необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.
Величину интенсивности внутренних сил в точке поперечного сечения называют механическим напряжением. Напряжение характеризует величину внутренней силы, приходящейся на единицу площади поперечного сечения.
Тема 2.1. Основные положения 171
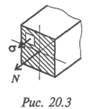
Рассмотрим брус, к которому приложена внешняя нагрузка (рис. 19.2). С помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие оставшейся правой части. Выделим на секущей плоскости малую площадку ΔА На этой площадке действует равнодействующая внутренних сил упругости. Направление напряжения рср совпадает с направлением внутренней силы в этом сечении.
Вектор рср называют полным напряжени ем. Его принято раскладывать на два вектора (рис. 19.3): τ — лежащий в площадке сечения и σ — направленный перпендикулярно площадке.
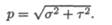
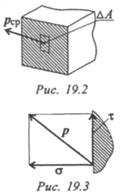Если вектор р — пространственный, то его раскладывают на три составляющие: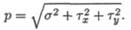 
Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.
Касательное напряжение характеризует сопротивление сечения сдвигу.
Сила N (продольная) вызывает появление нормального напряжения а. Силы Qx и Qy вызывают появление касательных напряжений т. Моменты изгибающие Мх и Му вызывают появление нормальных напряжений ст, переменных по сечению.
Крутящий момент Mz вызывает сдвиг сечения вокруг продольной оси, поэтому появляются касательные напряжения т.
Примеры решения задач
Пример 1. Определить величину продольной силы в сечении 1-1 (рис. 19.4).
Решение
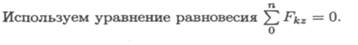
172 Лекция 19
Рассматривая левую часть бруса, определяем Nz1 = -12 + 8 - 5 = 9кН. Рассматривая правую часть бруса, определяем Nz1 =23 — 14 = 9кН.
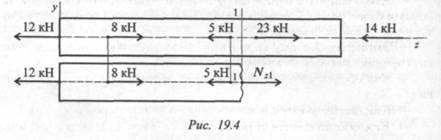
Величина продольной силы в сечении не зависит от того, какая часть бруса рассматривается.
Пример 2. Определить внутренний силовой фактор в сечении 1-1 (рис. 19.5а).
Решение
Контрольные вопросы и задания
1. Какие силы в сопротивлении материалов считают внешними?
Какие силы являются внутренними?
2. Какими методами определяют внешние силы? Как называют
метод для определения внутренних сил?
3. Сформулируйте метод сечений.
Тема 2.1. Основные положения 173
4. Как в сопротивлении материалов располагают систему координат?
5. Что в сопротивлении материалов называют внутренними силовыми факторами? Сколько в общем случае может возникнуть внутренних силовых факторов?
6. Запишите систему уравнений, используемую при определении внутренних силовых факторов в сечении?
7. Как обозначается и как определяется продольная сила в сечении?
8. Как обозначаются и как определяются поперечные силы?
9. Как обозначаются и определяются изгибающие и крутящий моменты?
10. Какие деформации вызываются каждым из внутренних силовых факторов?
11. Что называют механическим напряжением?
12. Как по отношению к площадке направлены нормальное и касательные напряжения? Как они обозначаются?
13. Какие напряжения возникают в поперечном сечении при действии продольных сил?
14. Какие напряжения возникают при действии поперечных сил?
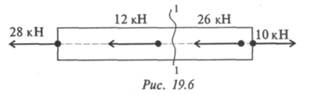
15. С помощью метода сечений определите величину внутреннего силового фактора в сечении 1-1 и вид нагружения (рис. 19.6).
16. С помощью метода сечений определите величину момента
m4, величину внутреннего силового фактора в сечении 2-2 и вид
нагружения (рис. 19.7).
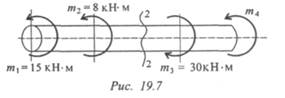
174 Лекция 19
17. Ответьте на вопросы тестового задания.
Тема 2.1. Основные положения, метод
сечений, напряжения
Тема 2.1. Основные положения 175
176 Лекция 20
ЛЕКЦИЯ 20
Тема 2.2. Растяжение и сжатие.
Внутренние силовые факторы, напряжения.
Построение эпюр
Иметь представление о продольных силах, о нормальных напряжениях в поперечных сечениях.
Знать правила построения эпюр продольных сил и нормальных напряжений, закон распределения нормальных напряжений в поперечном сечении бруса.
Уметь строить эпюры продольных сил и нормальных напряжений.
Растяжение и сжатие
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.
Продольные силы меняются по длине бруса. При расчетах после определения величин продольных сил по сечениям строится график — эпюра продольных сил.
Условно назначают знак продольной силы.
Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией (рис. 20.1а).
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией (рис. 20.16).
Примеры построения эпюры продольных сил
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).
Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами.
Тема 2.2. Растяжение и сжатие 177
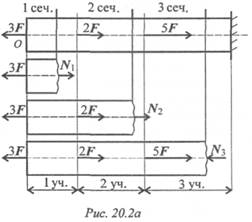На представленном рисунке 3 участка нагружения. Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Участок 1: ∑ Fz = 0; -3F + N 1 = 0; N 1 = 3F. Продольная сила положительна, участок 1 растянут.
Участок 2: ∑ Fz = 0; -3F + 2F + N 2 = 0; N 2 = F . Продольная сила положительна, участок 2 растянут.
Участок 3: ∑ Fz = 0; -3F + 2F + 5F - N3 = 0; N 3 = 4F . Продольная сила отрицательна, участок 3 сжат. Полученное значение N 3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.26).
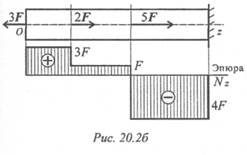Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz .
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.
178 Лекция 20
На эпюре проставляются значения Nz . Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.
Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
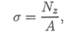где Nz — продольная cила в сечении; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46).
Тема 2.2. Растяжение и сжатие 179
Размерность (единица измерения) напряжений — Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа):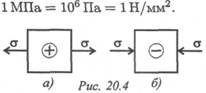 
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
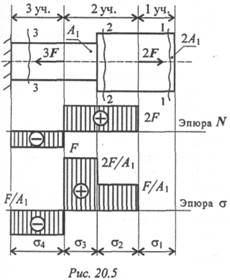
Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5).
Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1: N 1 = 0. Внутренние продольные силы равны нулю.
Участок 2: N 2 = 2F . Продольная сила на участке положительна.
Участок 3: N3 = 2F-3F = - F . Продольная сила на участке отрицательна.
Брус — ступенчатый. С учетом изменений величин площади поперечного сечения участков напряжений больше.
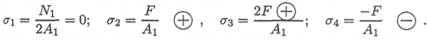
Строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
180 Лекция 20
Примеры решения задач
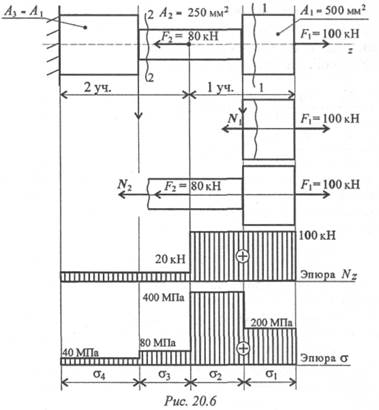
Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
1. Определяем участки нагружения, их два.
2. Определяем продольную силу в сечениях 1 и 2.
3. Строим эпюру.
4. Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
1. Определяем продольные силы.
Тема 2.2. Растяжение и сжатие 181
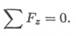
Сечение 1. – N1 + F1 = 0; N1 = F1 = 100 кН.
Сечение 2. -80 - N 2 + 100 = 0; N 2 = 100 - 80 = 20 кН.
В обоих сечениях продольные силы положительны.
Nz
2. Определяем нормальные напряжения σ = — .
A
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений. Нормальные напряжения в сечениях по участкам:
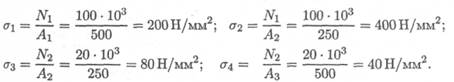
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Контрольные вопросы и задания
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
3. Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
4. Как распределены напряжения по сечению при растяжении и
сжатии?
5. Запишите формулу для расчета нормальных напряжений при
растяжении и сжатии.
6. Как назначаются знаки продольной силы и нормального напряжения?
7. Что показывает эпюра продольной силы?
8. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
9. В каких единицах измеряется напряжение?
182 Лекция 21
ЛЕКЦИЯ 21
Дата: 2018-12-21, просмотров: 829.
