Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 7.3),
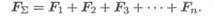
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Модуль равнодействующей пространственной системы сходящихся сил можно определить аналитически, использовав метод проекций.
52 Лекция 7
Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и суммируем соответствующие проекции (рис. 7.4). Получим проекции равнодействующей на оси координат:
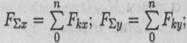
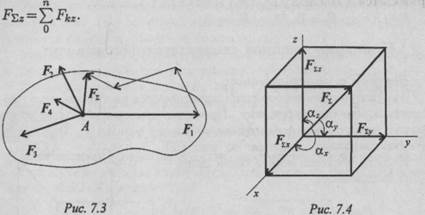
Модуль равнодействующей системы сходящихся сил определим по формуле
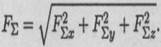
Направление вектора равнодействующей определяется углами
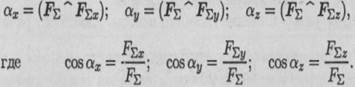
Произвольная пространственная система сил
Приведение произвольной пространственной системы сил к центру О
Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О.
Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения.
Тема 1.5. Пространственная система сил 53
В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) -Fгл (рис. 7.56).
Моменты пар сил можно сложить, получив суммарный момент системы Мгл (главный момент).
Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.
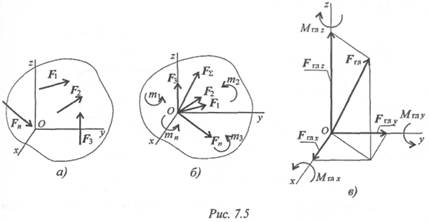
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 7.5в).
Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.
Абсолютное значение главного вектора (рис. 7.56) равно
54 Лекция 7
Уравнения равновесия пространственной системы сил
При равновесии Fгл = 0; Мгл = 0. Получаем шесть уравнений равновесия:
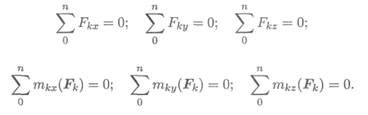
Шесть уравнений равновесия пространственной системы сил соответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей.
Примеры решения задач
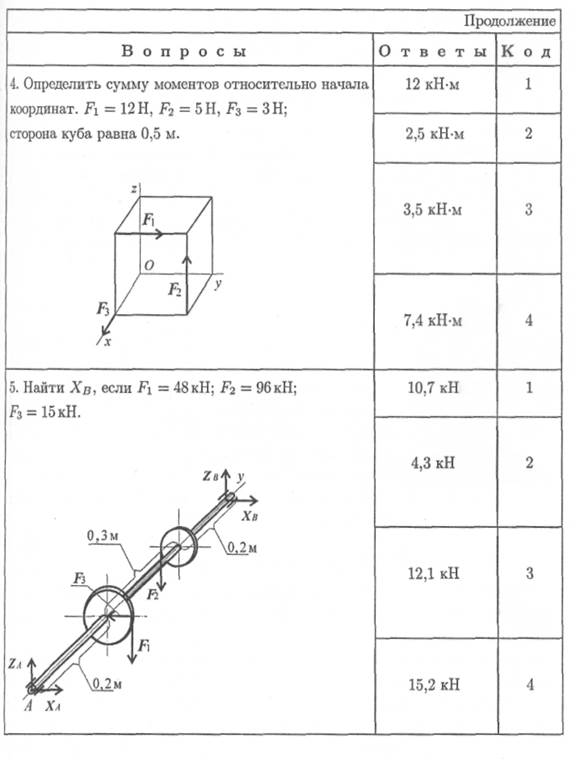
Пример 1. На тело в форме куба с ребром а — 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.
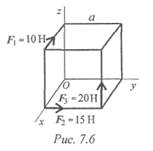
Решение
1. Моменты сил относительно оси Ох:
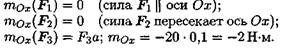
2. Моменты сил относительно оси Оу:
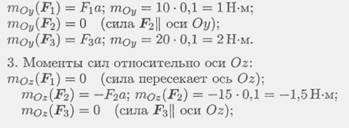
Тема 1.5. Пространственная система сил 55
Пример 2. На горизонтальном валу закреплены два колеса, r1 = 0,4 м; гз = 0,8 м. Остальные размеры — на рис. 7.7. К колесу 1 приложена сила F1, к колесу 2 — силы F 2 = 12 кН, F 3 = 4кН.
Определить силу F1 и реакции в шарнирах А и В в состоянии равновесия.
Напомним:
1. При равновесии выполняются шесть равнений равновесия.
Уравнения моментов следует составлять относительно опор А и В.
2. Силы F2 \\ Ox ; F1\\ Oy ; F3 \\Оу.
Моменты этих сил относительно соответствующих осей равны нулю.
3. Расчет следует завершить проверкой, использовав дополнительные уравнения равновесия.
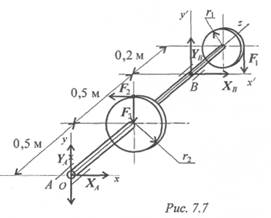
Решение
1. Определяем силу F 1 , составив уравнение моментов сил относительно оси Oz :
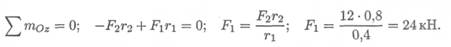
2. Определяем реакции в опоре А. На опоре действуют две составляющие реакции (Yа ;Х A ).
Составляем уравнение моментов сил относительно оси Ох' (в опоре B).
Поворот вокруг оси Ох' не происходит:
56 Лекция 7
Знак «минус» означает, что реакция направлена в противоположную сторону.
Поворот вокруг оси Оу' не происходит, составляем уравнение моментов сил относительно оси Оу' (в опоре В):
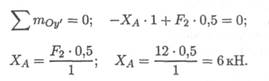
3. Определяем реакции в опоре В. На опоре действуют две составляющие реакции (Х В ; Yb ). Составляем уравнение моментов сил
относительно оси Ох (опора А):
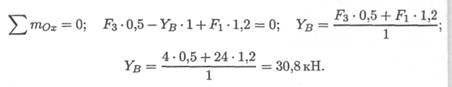
Составляем уравнение моментов относительно оси Оу (опора А):
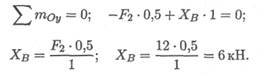
4. Проверка. Используем уравнения проекций:
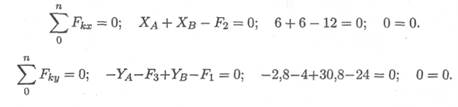
Расчет выполнен верно.
Контрольные вопросы и задания
1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил.
Тема 1.5. Пространственная система сил 57
2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил.
3. Запишите формулу для расчета главного момента пространственной системы сил.
4. Запишите систему уравнений равновесия пространственной системы сил.
5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R 1 (рис. 7.8)?
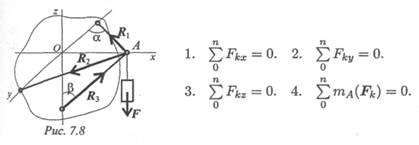
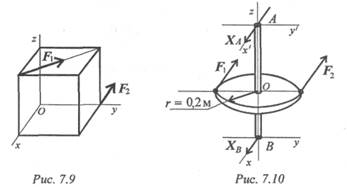
6. Определите главный момент системы сил (рис. 7.9). Точка
приведения — начало координат. Координатные оси совпадают с
ребрами куба, ребро куба равно 20 см; F 1 = 20 кН; F 2 = 30 кН.
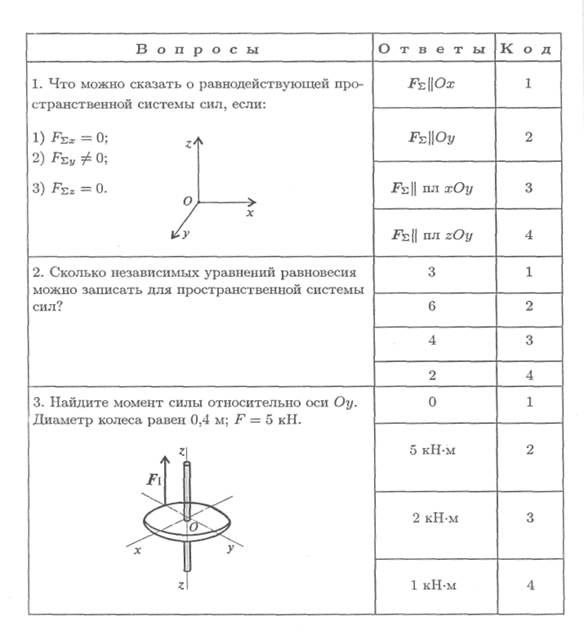
7. Определите реакцию Х В (рис. 7.10). Вертикальная ось со
шкивом нагружена двумя горизонтальными силами. Силы F1 и F 2 параллельны оси Ох. АО = 0,3 м; О B = 0,5 м; F 1 = 2 кН; F 2 = 3,5 кН.
Рекомендация. Составить уравнение моментов относительно оси Оу' в точке А.
58 Лекция 7
8. Ответьте на вопросы тестового задания.
Тема 1.5. Статика.
Пространственная система сил
Тема 1.5. Пространственная система сил 59
60 Лекция 8
ЛЕКЦИЯ 8
Тема 1.6. Центр тяжести
Иметь представление о системе параллельных сил и центре системы параллельных сил, о силе тяжести и центре тяжести.
Знать методы для определения центра тяжести тела и формулы для определения положения центра тяжести плоских фигур.
Уметь определять положение центра тяжести простых геометрических фигур, составленных из стандартных профилей.
Сила тяжести
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
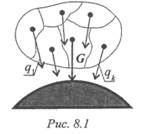
Точка приложения силы тяжести
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
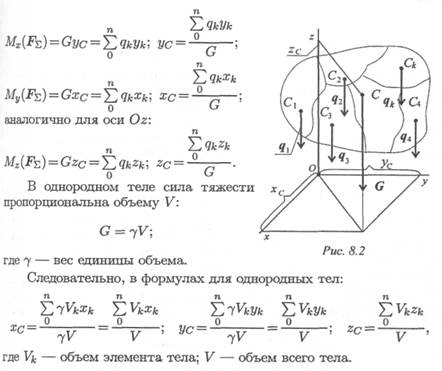
Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).
Тело состоит из частей, силы тяжести которых qk приложены в центрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре С.
ХС, УС, ZС — координаты центра тяжести С.
Xk , У k и Zk — координаты центров тяжести частей тела.
Тема 1.6. Центр тяжести 61
Из теоремы Вариньона следует:
Центр тяжести однородных плоских тел
(плоских фигур)
Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать: V = Ah , где А — площадь фигуры, h — ее высота.
Тогда после подстановки в записанные выше формулы получим:
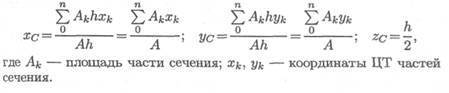
62 Лекция 8
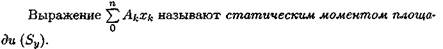
Координаты центра тяжести сечения можно выразить через статический момент:
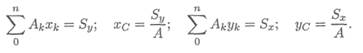
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Определение координат центра тяжести
плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).
При решении задач используются следующие методы:
Тема 1.6. Центр тяжести 63
1) метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько
простых частей, положение центров тяжести которых легко определить;
3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Примеры решения задач
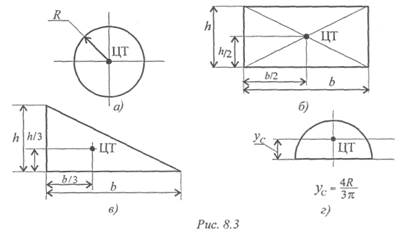
Пример 1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.
Решение
Пример 2. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).
Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.
Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих стандартах.
64 Лекция 8
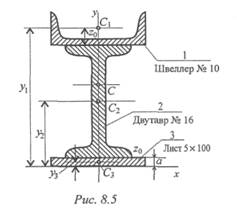
Решение
1. Обозначим фигуры номерами и выпишем из таблиц необходимые данные:
1 — швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А 1 = 10,9 см2;
2 — двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А 2 = 20,2 см2;
3 — лист 5x100; толщина 5 мм; ширина 100 мм; площадь сечения Аз = 0,5 • 10 = 5 см2.
2. Координаты центров тяжести каждой фигуры можно определить по чертежу.
Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата X с = 0.
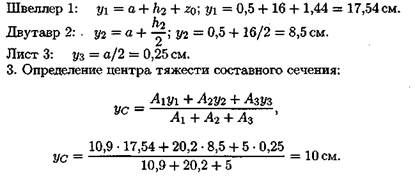
Тема 1.6. Центр тяжести 65
Контрольные вопросы и задания
1. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?
2. Запишите формулы для определения положения центра тяжести неоднородных и однородных тел, формулы для определения положения центра тяжести плоских сечений.
3. Повторите формулы для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга.
4. Что называют статическим моментом площади?
5. Вычислите статический момент данной фигуры относительно оси Ox . h = 30 см; b = 120 см; с = 10 см (рис. 8.6).
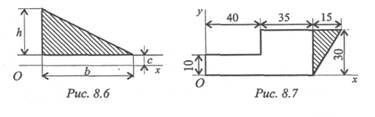
6. Определите координаты центра тяжести заштрихованной фигуры (рис. 8.7). Размеры даны в мм.
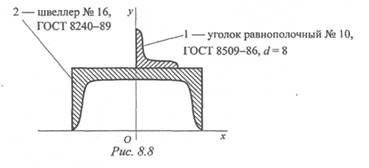
7. Определите координату у фигуры 1 составного сечения
(рис. 8.8).
При решении воспользоваться справочными данными таблиц ГОСТ «Сталь горячекатанная» (см. Приложение 1).
66 Лекция 9
ЛЕКЦИЯ 9
Тема 1.7. Основные понятия кинематики.
Кинематика точки
Иметь представление о пространстве, времени, траектории, пути, скорости и ускорении.
Знать способы задания движения точки [естественный и координатный).
Знать обозначения, единицы измерения, взаимосвязь кинематических параметров движения, формулы для определения скоростей и ускорений (без вывода).
Кинематика рассматривает движение как перемещение в пространстве. Причины, вызывающие движение, не рассматриваются. Кинематика устанавливает способы задания движения и определяет методы определения кинематических параметров движения.
Основные кинематические параметры
Траектория
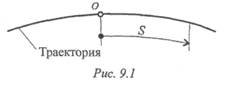
Линию, которую очерчивает материальная точка при движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой, плоской и пространственной линией.
Уравнение траектории при плоском движении: у = f ( x ).
Пройденный путь
Путь измеряется вдоль траектории в направлении движения. Обозначение — S , единицы измерения — метры.
Уравнение движения точки
Уравнение, определяющее положение движущейся точки в зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки, рассмат-
Тема 1.7. Основные понятия кинематики 67
риваемой как начало отсчета (рис. 9.1). Такой способ задания движения называется естественным.
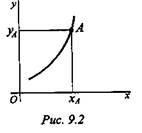
Таким образом, уравнение движения можно представить в виде S = f ( t ). Положение точки можно также определить, если известны ее координаты в зависимости от времени (рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения: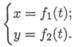 
В случае пространственного движения добавляется и третья координата z= f3( t ).
Такой способ задания движения называют координатным.
Скорость движения
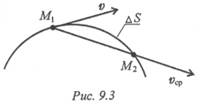
Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.
Скорость — вектор, в любой момент направленный по касательной к траектории в сторону направления движения (рис. 9.3).
Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным. Средняя скорость на пути AS определяется как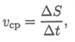 
где AS — пройденный путь за время Д*; At — промежуток времени.
Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным.
В этом случае скорость — величина переменная и зависит от времени v = f ( t ).
При рассмотрении малых промежутков времени (∆ t —► 0) средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как
68 Лекция 9
производную пути по времени:
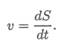
За единицу скорости принимают 1 м/с. Иногда скорость измеряют в км/ч,
1000
1 км/ч = ------ = 0,278 м/с.
3600
Ускорение точки
Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.
Скорость точки при перемещении из точки М 1 в точку M 2 меняется по величине и направлению. Среднее значение ускорения за этот промежуток
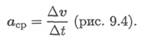
При рассмотрении бесконечно малого промежутка времени среднее ускорение превратится в ускорение в данный момент:
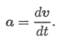
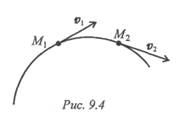
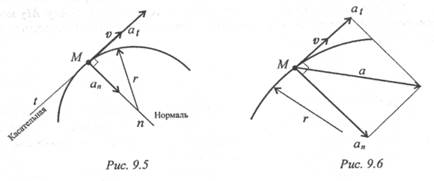
Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное (рис. 9.5).
Нормальное ускорение ап характеризует изменение скорости по направлению и определяется как
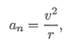
где г — радиус кривизны траектории в данный момент времени.
Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги.
Касательное ускорение аt характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а
Тема 1.7. Основные понятия кинематики 69
при замедлении оно направлено противоположно направлению вектора скорости.
Формула для определения касательного ускорения имеет вид:
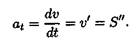
Значение полного ускорения определяется как
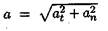(рис. 9.6).
Примеры решения задач
Пример 1. Дано уравнение движения точки: S = 0,36t2 + 0,18t. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые 3 секунды.
Решение
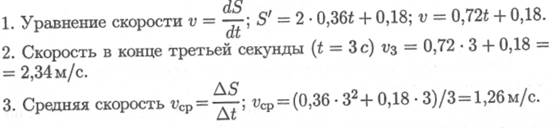
Пример 2.
Точка движется по кривой радиуса r = 10 м согласно уравнению S = 2,5t2 + 1,2t + 2,5 (рис. 9.6).
70 Лекция 9
Определить полное ускорение точки в конце второй секунды движения и указать направление касательной и нормальной составляющих ускорения в точке М.
Решение
d v
1. Касательное ускорение определяется как at = —.
dS d t
Уравнение скорости: v = ---- .
dt
Скорость будет равна v = 2 • 2,5 t + 1,2; v = 5 t + 1,2 (м/с).
Касательное ускорение: at = v' = 5 м/с² .
Вывод: касательное ускорение не зависит от времени, оно постоянно.
v²
2. Нормальное ускорение: ап = —.
r
Скорость на второй секунде будет равна v 2 = 5 ∙ 2+1,2 = 11,2 м/с.
(11,2)²
Величина нормального ускорения: аn2 = ——— = 12,54 м/с² .
10
3. Полное ускорение: а = √ a t²+ an².
Полное ускорение в конце второй секунды:
а2 = √52 + 12,542 = 13,5 м/с2.
4. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.
Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, т. к. касательное ускорение — положительная величина (скорость растет).
Контрольные вопросы и задания
1. Запишите в общем виде закон движения в естественной и координатной форме.
2. Что называют траекторией движения?
3. Как определяется скорость движения точки при естественном способе задания движения?
4. Запишите формулы для определения касательного, нормального и полного ускорений.
5. Что характеризует касательное ускорение и как оно направлено по отношению к вектору скорости?
6. Что характеризует и как направлено нормальное ускорение?
Тема 1.8. Кинематика точки 71
ЛЕКЦИЯ 10
Тема 1.8. Кинематика точки
Иметь представление о скоростях средней и истинной, об ускорении при прямолинейном и криволинейном движениях, о различных видах движения точки.
Знать формулы (без вывода) и графики равномерного и равнопеременного движений точки.
Уметь определять параметры движения точки по заданному закону движения, строить и читать кинематические графики.
Дата: 2018-12-21, просмотров: 1607.
