Жидкость, заключенная в неподвижный резервуар и находящаяся в равновесии под действием силы тяжести, пребывает в абсолютном покое относительно земли.
Жидкость может быть в равновесии и при действии других внешних сил, помимо собственного веса. Жидкое тело в таком случае будет находиться в относительном покое. При равновесии в движущихся сосудах жидкость движется вместе с ними как твердое тело. Если резервуар движется прямолинейно с постоянным ускорением, то свободная поверхность будет представлять собой плоскость, наклоненную к горизонту под углом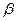 
. Тангенс данного угла определяется по следующей формуле
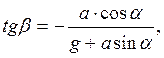(4.1)
где а – ускорение при движении,
g – ускорение свободного падения,
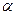- угол наклона к горизонту вектора ускорения.
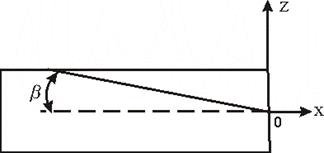
Рис. 4.1
При движении резервуара с постоянным ускорением 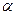давление в точках, находящаяся на глубине h под свободной поверхностью, на котором действует давление Р0, может быть определено по формуле
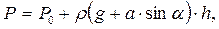(4.2)
где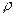 
- плотность жидкости,
а - ускорение,
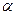- угол наклона к горизонту вектора ускорения,
h – глубина погружения точки под свободной поверхностью,
Р0 – давление, действующее на свободную поверхность.
В случае, когда резервуар открыт в атмосферу, избыточное давление на глубине h под свободной поверхностью определяется
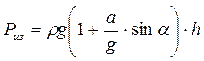(4.3)
При равновесии жидкости в сосуде, равномерно вращаемся относительно вертикальной оси, свободная поверхность представляет собой параболоид вращения, уравнение которой имеет вид
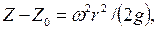(4.4)
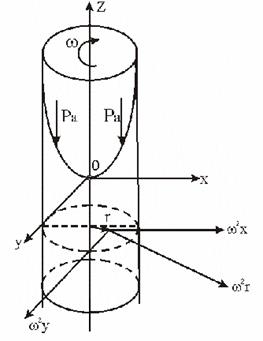
Рис. 4.2
где Z0 – вертикальная координата вершины параболоида,
Z – координаты любой точки свободной поверхности,
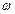- угловая скорость вращения резервуара,
r – радиус.
Высота параболоида определяется по формуле
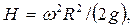(4.5)
где R – радиус сосуда.
Закон распределения давления в жидкости выражается уравнением
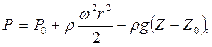(4.6)
где Р0 – давление в точках параболоида поверхности уровня, вертикальная координата вершины которого равна Z0,
Р – давление в произвольной точке жидкости с координатами r и Z.
Для преодоления положения свободной поверхности используются следующие соображения:
а) объем параболоида вращения равен половине произведения площади его основания на высоту.
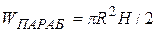(4.7)
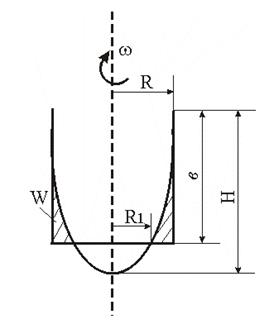
Рис. 4.3
б) объем жидкости, когда свободная поверхность пересекает дно сосуда, определяется по формуле
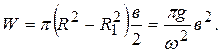(4.8)
Осевая сила жидкости на стенку определяется по формуле
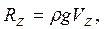(4.9)
где Vz – объем тела давления, построенного параллельно направлению Z между стенкой и пьезометрической поверхностью.
Пример. Имеется цилиндрический резервуар диаметром D 1 и высотой L, имеющий в верхней крышке отверстие диаметром D 2, заполненный жидкостью до высоты В. Необходимо определить угловую скорость вращения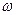 
и силу давления жидкости на закраину.
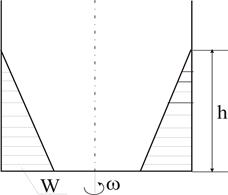
В зависимости от объема жидкости вершина параболоиды свободной поверхности может располагаться ниже (1) или выше (3) дна, а также пересекать дно резервуара (2).
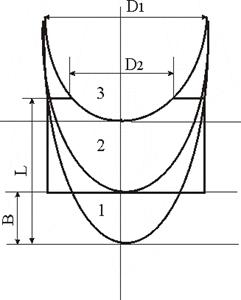
Рис. 4.4
Угловая скорость определяется:
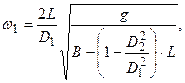(4.10)
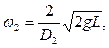(4.11)
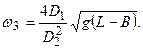(4.12)
Объем жидкости, при котором вершина касается дна резервуара, можно определить по формуле
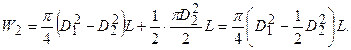(4.13)
Высота заполнения в таком случае
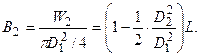(4.14)
Необходимо сравнивать заданную высоту заполнения сосуда с полученным критическим значением В2. Определить, какому из трех случаев соответствует заданный, а затем, выбрав одну из трех формул, определить угловую скорость.
Сила давления жидкости на закраину вычисляется по формуле, в которой объем тела давления определяется по формуле
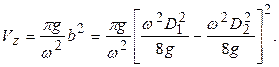(4.15)
Система задач на тему: “Относительный покой жидкости”
1 2
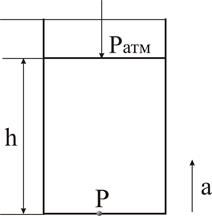
Дано: сосуд движется с ускорением Дано: h = 1м, а = 0,5g
a = 450 Найти: Давление Р, действующее
Найти: b - угол наклона свободной на дно резервуара поверхности
3
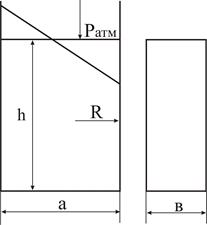
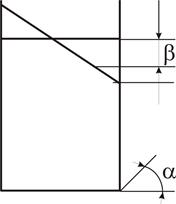
Дано: сосуд движется горизонтально с ускорением
а = 10 м/с2
h = 4м
а = 2м
в = 1м
Найти: силу избыточного давления
жидкости на боковую поверхность
4 5
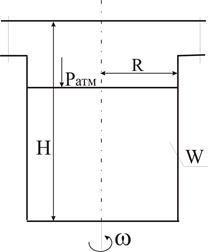
Дано: W = 0,25м3 Дано: R = 0,4м, Н = 0,7 м,
w = 5,5 рад/с W = 0,25м2 , w = 10 рад/с
Найти: h Найти: усилие на верхнюю стенку
5. Режимы движения жидкости.
Движение жидкости происходит не всегда одинаково. Детальные экспериментальные исследования режимов движения жидкости выполнил английский физик О. Рейнольдс. В ходе своих опытов, он выяснил, что при малых скоростях движение жидкости имеет упорядоченный слоистый характер. При более высоких скоростях происходит перемешивание частиц жидкости, и движение становится беспорядочным.
Режим движения, при котором имеет место слоистые движение жидкости, называется ламинарным, хаотическое движение называется турбулентным.
Критерием перехода с ламинарного режима к турбулентному является число Рейнольдса – безразмерный численный параметр, не зависящий от рода жидкости и размеров живого сечения потока.
Определяется число Рейнольдса по формуле
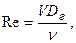(5.1)
где V – средняя скорость движения жидкости,
D г – гидравлический диаметр, определяемый по формуле
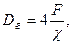(5.2)
где F - площадь сечения потока,
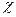- периметр сечения,
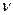- кинематическая вязкость жидкости.
Для трубопроводов, состоящих из круглых труб число Рейнольдса может быть определено по формуле
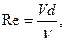(5.3)
где d – диаметр трубопровода.
Принимается расчетное критическое число Рейнольдса для трубопроводов
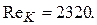(5.4)
Для определения режима движения жидкости в конкретных условиях необходимо установить действительное число Рейнольдса по формуле (5.1) или (5.3), затем полученное число сравнивается с критическим и определяется режим движения
при Re < ReK = 2320 - режим движения ламинарный,
при Re > ReK = 2320 - режим движения турбулентный.
Дата: 2018-12-21, просмотров: 348.
