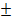| № п/п | Способ определения объема ствола | Объем, м3 | Ошибки | ||||
| в коре | без коры | Абсолютные | Относительные | ||||
| в коре | без коры | в коре | без коры | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | По сложной формуле срединных сечений | 0,6005 | 0,5229 | - | - | - | - |
| 2 | По простой формуле срединного сечения | 0,5645 | 0,5187 | - 0,036 | - 0,0042 | - 6,0 | - 0,8 |
| 3 | По двум концевым сечением | 0,8892 | 0,6434 | +0,2887 | +0,1205 | +48,1 | +23,0 |
Объем вычисленный по сложной формуле срединных сечений, принимаем за истинное условно точное значение, а объемы, вычисленные по простой формуле срединного сечения и формуле концевых сечений – за измеренные. Величина и знак абсолютной ошибки определяется путем вычитания из измеренного результата истинно точного результата.
В нашем примере абсолютная ошибка равна:
 V2 в коре = 0,5645 м3 – 0,6005 м3 = - 0,0360 м3
V2 в коре = 0,5645 м3 – 0,6005 м3 = - 0,0360 м3
 V3 в коре = 0,8892 м3 – 0,6005 м3 = + 0,2887 м3
V3 в коре = 0,8892 м3 – 0,6005 м3 = + 0,2887 м3
 V2 без коры = 0,5187 м3 – 0,5229 м3 = - 0,0042 м3
V2 без коры = 0,5187 м3 – 0,5229 м3 = - 0,0042 м3
 V3 без коры = 0,6434 м3 – 0,5229 м3 = + 0,1205 м3
V3 без коры = 0,6434 м3 – 0,5229 м3 = + 0,1205 м3
Относительная ошибка равна:
Р∆V = 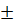
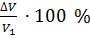
Р∆V2в коре = 
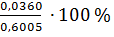 = - 6,0 %
= - 6,0 %
Р∆V3 в коре = 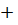
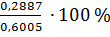 = + 48,1 %
= + 48,1 %
Р∆V2без коры = 
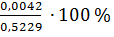 = - 0.8 %
= - 0.8 %
Р∆V3 без коры= 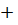
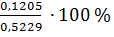 = + 23,0 %
= + 23,0 %
Задача № 26 (примеры вычислений)
Диаметры ствола на ¼, ½, ¾ высоты ствола определяем методом интерполяции.
Для этого определяем высоту ствола ¼, ½, ¾ части от его полной высоты; в нашем примере высота равна – 25,6 м
Н1/4 = 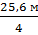 = 6,4 м
= 6,4 м
Н1/2 = 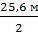 = 12,8 м
= 12,8 м
Н3/4 = 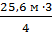 = 19,2 м
= 19,2 м
1. Определяем диаметры:
d1|4 = d6,4 (в коре) = d 5 - 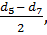 l = 22,0 см –
l = 22,0 см – 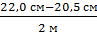 × 1,4 м = 20,95 см = 21,0 см
× 1,4 м = 20,95 см = 21,0 см
l = 6,4 м – 5,0 м = 1,4 м
d1/2 = d12,8 (в коре) = d11 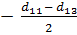 × l = 18,0 см -
× l = 18,0 см - 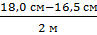 ×1,8 м = 16,7 см
×1,8 м = 16,7 см
l = 12,8 м – 11 м = 1,8 м
d3/4 = d19,2 (в коре) = d19  × L = 12,0 -
× L = 12,0 -  × 0,2 м = 11,7 см
× 0,2 м = 11,7 см
L = 19,2 м – 19 м = 0,2 м
2. Коэффициенты формы вычисляем в коре с точностью до 0,01, используем вычисленные диаметры на относительных высотах (диаметры пня и d1.3 берем из задания к задачам 1-25 таблицы 2).
q0 = 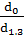 =
=  = 1,17
= 1,17
q1 = 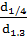 =
=  = 0,80
= 0,80
q2 = 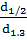 =
=  = 0,64
= 0,64
q3 = 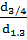 =
=  = 0,45
= 0,45
По значению «q2» устанавливаем степень сбежистости ствола, согласно таблице.
| Степень сбежистости стволов | Значение «q2» |
| Сбежистые | 0,155-0,60 |
| Среднесбежистые | 0,65-0,70 |
| Малосбежистые | 0,75-0,80 |
В нашем примере ствол – среднесбежистый.
3. Определяем значения видовых чисел с точностью до 0,001 по связям:
а) Кунце
f = q2 – C
C – постоянная величина, равная для: сосны – 0,20; ели, липы – 0,21; осины – 0,24; березы, лиственницы, бука, ольхи – 0,22.
В нашем примере: f = 0,64 – 0,20 = 0,440
б) Вейзе
f = q22 = 0,642 = 0,64 × 0,64 = 0,410
в) Шустова
f = 0,60 × q2 + 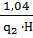
Н – высота дерева, в нашем примере – 25,6 м.
f = 0,60 × 0,64 + 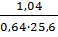 = 0,384 + 0,063 = 0,447
= 0,384 + 0,063 = 0,447
г) Шиффеля
f = 0,66 × q22+ 0,140 + 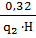
f = 0,66 × 0,642 + 0,140 + 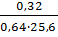 = 0,270 + 0,140+ 0,020 = 0,430
= 0,270 + 0,140+ 0,020 = 0,430
д) Видовое число по таблице Ткаченко определяем в приложении 10 по значению q2 и h.
В нашем примере q2= 0,64, h = 25,6 м
f = 0,433
е) вычисляем «старое» видовое число по формуле:
f =  =
= 
f =  =
= 
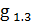 - площадь сечения на высоте груди, определяется l приложении 1 по диаметру в коре на высоте 1,3 м, в нашем примере он равен – 26,0 см.
- площадь сечения на высоте груди, определяется l приложении 1 по диаметру в коре на высоте 1,3 м, в нашем примере он равен – 26,0 см.
Н – высота ствола, в нашем примере равна 25,6 м.
Таблица 8
Сравнение полученных результатов видовых чисел, определенных
Разными способами
| № п/п | Способ определения видового числа | Значение видового числа | Ошибки | |
| Абсолютные | Относительные | |||
| 1 | По связи Кунце | 0,440 | - 0,002 | - 0,5 |
| 2 | По связи Вейзе | 0,410 | - 0,032 | - 7,2 |
| 3 | По связи Шустова | 0,447 | +0,005 | + 1,1 |
| 4 | По связи Шиффеля | 0,430 | - 0,012 | - 2,7 |
| 5 | По таблицам Ткаченко | 0,433 | - 0,009 | - 2,0 |
| 6 | «Старое» видовое число | 0,442 | - | - |
 f1 = 0, 440 – 0,442 = - 0,002
f1 = 0, 440 – 0,442 = - 0,002
Рf 1 = - 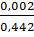 × 100 %= - 0,5 % и т. д.
× 100 %= - 0,5 % и т. д.
За истинное условно точное значение принимаем «старое» видовое число. Отклонения от истинного значения составляют не более 7,2 %.
Задача № 27 (примеры вычислений)
Определение объема растущего дерева приближенными способами подробно описано в учебнике (2), с. 59-61, (3), с. 49-51.
а) определение объема ствола растущего дерева по общей формуле через видовое число:
Vств. =  1,3 × h ×f
1,3 × h ×f
Значение  берем из приложения 1 (площади поперечных сечений), согласно диаметра на высоте груди 1,3 м, в коре, в нашем примере равен – 26 см;
берем из приложения 1 (площади поперечных сечений), согласно диаметра на высоте груди 1,3 м, в коре, в нашем примере равен – 26 см; 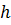 - высота дерева, равна 25,6 м; f – видовое число из приложения 10 таблицы видовых чисел Ткаченко по значению
- высота дерева, равна 25,6 м; f – видовое число из приложения 10 таблицы видовых чисел Ткаченко по значению 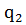 и
и 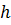 ; среднее значение
; среднее значение 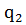 для древесных пород: сосна – 0,67; ель, пихта – 0,70; дуб – 0,68; береза, бук - 0,66; осина – 0,70; ольха черная – 0,69.
для древесных пород: сосна – 0,67; ель, пихта – 0,70; дуб – 0,68; береза, бук - 0,66; осина – 0,70; ольха черная – 0,69.
Vств = 0,0531 м2 × 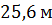 × 0,458 = 0,6226 м3
× 0,458 = 0,6226 м3
б) определение объема ствола по формуле Денцина
Vств =0,001 × 
Эта формула приближенно верна для следующих высот: сосны – 30 м, ели, бука, дуба – 26 м, пихты – 25 м. Если фактические высоты будут больше или меньше этих значений, то на каждый лишний метр высоты следует прибавить или убавить следующий процент от полученного объема: для сосны 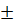 3 %, ели, пихты
3 %, ели, пихты 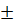 3-4 %; дуба, бука
3-4 %; дуба, бука 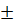 5 %.
5 %.
В нашем примере диаметр на высоте груди 1,3 м в коре 26 см, порода сосна, h = 25,6 м
Vств =0,001×262 = 0,6760 м3
Поправка: 30 м – 25,6 м = 4,4 ×3 % = 13,2 %,
что составит 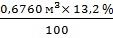 = 0,0892 м3
= 0,0892 м3
Объем ствола с учетом поправки будет равен:
Vств =0,6760 м3 - 0,0892 м3 = 0,5868 м3
Задача № 28 (примеры вычислений)
По исходным данным, приведенным в таблице 2, определяем:
1. Средний прирост  т =
т = 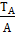
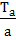
где:
 т – средний прирост по какому-либо показателю;
т – средний прирост по какому-либо показателю;
ТА- значение таксационного показателя в возрасте А (лет);
А – возраст дерева (древостоя), лет
по высоте  h =
h =  =
= 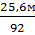 = 0,28 м
= 0,28 м
по диаметру  d1.3 =
d1.3 = 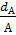 =
=  = 0,25 см
= 0,25 см
по объему  V =
V = 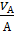 =
= 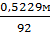 = 0,0057м3
= 0,0057м3
VА = 0,5229 м3 взят из таблицы 6 без коры.
2. Текущий среднепериодический прирост:
 п
п 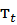 =
= 
 п
п 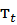 - текущий среднепериодический прирост;
- текущий среднепериодический прирост;
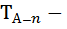 значение таксационного показателя в возрасте предшествующем периоду n
значение таксационного показателя в возрасте предшествующем периоду n
n – число лет в периоде (равно 10)
по высоте:.  пh =
пh =  =
= 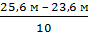 = 0,20 м
= 0,20 м
 =
= 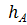 -
-  п
п 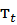 = 25,6м – 2,0м = 23,6 м
= 25,6м – 2,0м = 23,6 м
 пh - текущий периодический прирост по высоте за 10 лет взят из таблицы 2
пh - текущий периодический прирост по высоте за 10 лет взят из таблицы 2
по диаметру:  пd 1.3 =
пd 1.3 = 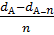 =
= 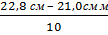 = 0,18 см
= 0,18 см
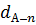 = dА-
= dА- 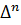 d1,3 = 22,8 – 1,8см = 21,0см
d1,3 = 22,8 – 1,8см = 21,0см
по объему:  пv =
пv = 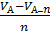 =
=  = 0,0130 м3
= 0,0130 м3
объемы  и
и  - взяты из таблицы 6.
- взяты из таблицы 6.
3. Процент текущих приростов (Р):
Р = 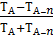 ×
× 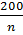
по высоте: Рh =  ×
× 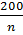 =
= 
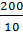 × = 0,8 %
× = 0,8 %
по диаметру: Рd1.3 = 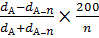 =
= 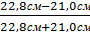
 = 0,8 %
= 0,8 %
по объему: РV = 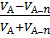
 =
=  = 2,8 %
= 2,8 %
4. У растущего дерева процент объемного прироста можно определить через относительный диаметр (dот) и группу роста (способ Пресслера)
dот = 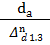 =
=  = 12,7 см
= 12,7 см
Группа роста определяется по энергии роста и протяженности кроны в приложении 8. В нашем примере рост умеренный, крона занимает положениe между ½ - ¾ высоты, значит группа роста III ½. У нас относительный диаметр 12,7 см, группа роста III ½, поэтому делаем интерполяцию, используя приложение 8.
Для III группы роста дерева на 1 единицу расхождение составляет:
(22 – 21) : 5 = 0,2 %
Для IV группы роста дерева на 1 единицу расхождение составит:
(25 – 24) : 5 = 0,2 %
При группе роста дерева III и относительном диаметре 12,7 см процент текущего прироста будет равен:
(22 – 0,2 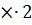 ) = 22 – 0,4 = 21,6 %
) = 22 – 0,4 = 21,6 %
При группе роста дерева IV и относительном диаметре 12,7см процент текущего прироста будет равен:
(25-0,2  ) = 25-0,4 = 24,6 %
) = 25-0,4 = 24,6 %
Для III1/2 группы роста % текущего периода прироста равен:
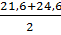 = 23,1 %
= 23,1 %
а за один год равен 23,1 % : 10 = 2,31 % = 2,3 %
5. Высоту дерева в возрасте 10 лет определяем методом арифметической интерполяции.
В нашем примере число годичных слоев на пне – 92; на 1,3 м – 82; на 3 м – 75
Отсюда следует, что:
За 92-86 = 6 лет дерево выросло на 1,3 м
За 92-79 = 13 лет дерево выросло на 3,0 м.
Тогда h10 = h13 - 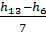 × 3 = 3 -
× 3 = 3 - 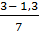 × 3= 3 м-0,73 м = 2,27 м
× 3= 3 м-0,73 м = 2,27 м 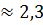 м.
м.
Задачи № 29-53
Исходные данные этих задач представлены в таблице 3.
Дата: 2018-12-21, просмотров: 839.