(задачи № 1-103)
Задачи № 1-25 (примеры вычислений)
1. Определяем объем ствола срубленного дерева в коре и без коры в настоящее время и 10 лет назад без коры по сложной формуле срединных сечений по форме таблицы 6.
Все решения проводятся по 0 варианту. Исходные данные студенты заносят в таблицу 6 из таблицы 2, заполняя графы 1, 2, 3, 4. Диаметр 10 лет назад (графа 5) определяем путем вычитания прироста по диаметру за 10 лет (графа 4) из диаметра без коры (графа 3). В нашем примере диаметр 10 лет назад на высоте 1 м от основания ствола будет равен 23,8-1,9 м = 21,9 см.
Объемы двухметровых отрезков в коре, без коры, 10 лет назад без коры определяем в приложении 2 методических указаний, согласно диаметров в коре, без коры, 10 лет назад на нечетных метрах (серединах двух метровых секций).
Так для диаметра в коре на высоте сечения 1 м (27,0 см) объем двухметрового отрезка по приложению 2 будет 0,1145 м3, а для диаметра без коры (23,8 см) – 0,0889 м 3, для диаметра 10 лет назад (21,9 см) – 0,0753 м3.
Вершину отсекаем на последнем четном метре (24 м). Длину вершины определяем как разность между высотой ствола 25,6 м и длиной ствола без вершинки, равной 24 м, длина вершины будет равна 25,6 м – 24 м = 1,6 м.
Объем вершины определяем по формуле объема Vвер =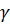 
n+1 
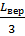
n-1 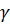– площадь сечения основания вершины, определяется в приложении 1 методических указаний, согласно диаметров основания вершины в коре и без коры, так для диаметра в коре (3,5 см), 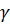n+1 =9,6 см2 = 0,00096 м2;
Для диаметра без коры (2,5 см), 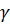n+1 = 4,9 см2 = 0,00049 м2.
Вариант «0»
Порода – сосна
Возраст – 92 года
Высота ствола – 25,6 м
Длина кроны – 10 м
Энергия роста в высоту – рост умеренный
Прирост по высоте за 10 лет – 2,0 м
Число годичных слоев на высоте 1,3 м – 86
Число годичных слоев на высоте 3 м – 79
Таблица 6
| Высота сечения ствола, м | Диаметр, см | Прирост по диаметру за 10 лет, см | Диаметр 10 лет назад, см | Объем двухметровых отрезков | |||
| в коре | без коры | в коре | без коры | 10 лет назад | |||
| 1.3 0 (на пне) 1 3 5 7 9 11 13 15 17 19 21 23 | 26,0 30,5 27,0 23,5 22,0 20,5 19,0 18,0 16,5 15,5 13,5 12,0 9,0 5,5 | 22,8 26,0 23,8 21,4 20,5 19,5 18,2 17,3 15,8 15,0 13,0 11,5 8,5 5,0 | 1,8 2,3 1,9 2,1 2,2 2,3 2,3 2,5 2,5 2,7 2,7 2,8 2,9 2,9 | - - 21,9 19,3 18,3 17,2 15,9 14,8 13,3 12,3 10,3 8,7 5,6 2,1 | - - 0,1145 0,0867 0,0760 0,0660 0,0567 0,0509 0,0428 0,0377 0,0286 0,0226 0,0127 0,0048 | - - 0,0889 0,0719 0,0660 0,0597 0,0520 0,0470 0,0392 0,0353 0,0265 0,0208 0,0114 0,0039 | - - 0,0753 0,0584 0,0526 0,0465 0,0397 0,0344 0,0278 0,0238 0,0167 0,0119 0,0049 0,0007 |
| Итого по 2х м отрезкам | 0,6000 | 0,5226 | 0,3927 | ||||
| Основание вершинки | 3,5 | 2,5 | |||||
| Объем вершинки | 0,0005 | 0,0003 | - | ||||
| Общий объем ствола | 0,6005 | 0,5229 | 0,3927 | ||||
Объем вершинки в коре Vв коре = 0,00096 м2 ×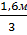 
= 0,0005 м3
Объем вершинки без коры V без коры = 0,00049 м2 × 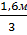= 0,0003 м3
Все данные расчетов заносим в таблицу 6. Сложив в таблице 6 по вертикали объемы двухметровых отрезков в коре, без коры, 10 лет назад и объемы вершинки, получим общий объем ствола в коре – 0,6005 м3; без коры – 0,5229 м3; объем 10 лет назад без коры – 0,3927 м3.
2. Определяем объем ствола по простой формуле срединного сечения
V = 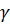× L + Vвер
где L – длина ствола от основания до вершинки, в нашем примере – 24,0 м.
Vвер – объем вершинки.
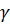- площадь сечения на ½ длины ствола без вершинки, для её определения необходимо найти диаметр на половине длины ствола без вершины
(24 м : 2 =12 м), его мы находим:
d12 (в коре) =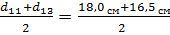 
= 
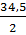= 17,25 см = 17,3 см
d12 (без коры) 
= 
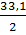= 16,55 см = 16,6 см
по приложению 1 находим по вычисленным диаметрам площади сечений на половине длины ствола без вершины
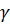1/2 в коре = 0,0235 м2
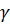1/2 без коры = 0,0216 м2
Тогда объем ствола в нашем примере по простой формуле срединного сечения равен
Vв коре = 0,0235 м2 × 24 м + 0,0005 м3 = 0,5645 м3
Vбез коры = 0,0216 м2 × 24 м + 0,0003 м3 = 0,5187 м3
3. Определяем объем ствола по двум концевым сечениям
V =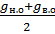 
× L + Vвер
где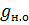 
- площадь сечения нижнего основания, определяется по диаметрам в коре и без коры на 0 (на пне);
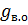- площадь сечения верхнего основания, определяется по диаметрам в коре и без коры основания вершины, т.е. на четном метре. Используем приложение 1.
В нашем примере диаметр в коре на пне – 30,5 см, без коры – 26,0 см, согласно этим диаметрам
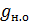(в коре) = 0,0731 м2; 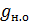(без коры) = 0,0531 м2;
Диаметр в коре на четном метре – 3,5 см; без коры - 2,5 см,
согласно этим диаметрам 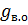(в коре) = 0,00096м2, 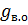(без коры) = 0,00049м2
В нашем примере объем равен:
Vв коре =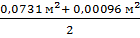 
× 24 м + 0,0005 м3 = 0,8892 м3
Vбез коры =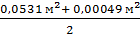 
× 24 м + 0,0005 м3 = 0,6434 м3
1. Результаты определения объемов ствола разными способами заносим в таблицу
Сравнение и анализ полученных результатов определения
Дата: 2018-12-21, просмотров: 624.
