Решают 2 задачи: прямую и обратную.

При прямой задаче по известному исходному звену (его номинальному значению, допуску и предельным отклонениям) определяют номинальные размеры, допуски и предельные отклонения всех составляющих звеньев, задача решается на стадии проектных расчетов. (известно A_∆, TA_∆, ESA_∆, EIA_∆

Определяют А₁, А₂, А₃ … А_і, TA_і, ESA_і, EIA_і).

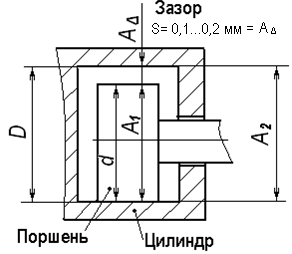
Пример. Из функционального назначения соединения определили, что величина зазора S в паре трения поршень-цилиндр должна быть от 0,1 до 0,2мм, т.е. замыкающее звено можно представить в виде A_∆ = 0,1 ^+0,1.

При решении определяют А₁, А₂; TA₁, TA₂; ESA₁, EIA₁, ESA₂, EIA₂.

 При обратной задаче по известным составляющим звеньям (номинальным размерам, допускам и предельным отклонениям) определяется номинальное значение, допуск и отклонение замыкающего звена.

Известно: А_і, TA_і, ESA_і, EIA_і;

Находят: A_∆, TA_∆, ESA_∆, EIA_∆.

Методы достижения точности замыкающего звена

1. Метод полной взаимозаменимости

2. Метод неполной взаимозаменимости

3. Метод групповой взаимозаменимости

4. Регулирования

5. Пригонки

Методы расчета размерных  цепей

1. Метод максимума и минимума обеспечивает полную взаимозаменяемость

2. Теоретико-вероятностный метод расчета обеспечивает неполную взаимозаменяемость.

3.Решение размерных цепей методом полной взаимозаменимости ( максимума и минимума)

При методе полной взаимозаменяемости точность замыкающего звена обеспечивается у всех изделий без исключения, без предварительного подбора или пригонки звеньев.

Этот метод еще носит название максимума и минимума, т.к. даже при самых неблагоприятных сочетаниях размеров составляющих звеньев точность замыкающего звена должна обеспечиваться. Сборка изделий заключается в простом соединении деталей и является самой дешевой из всех возможных (время сборки минимально).

Недостатки:

- используется для расчета размерных цепей с количеством звеньев до 5.

- составляющие звенья цепи имеют достаточно малые допуски, что повышает себестоимость изготовления деталей.

При решении размерных цепей используется понятие координаты середины поля допуска Е_сА_∆

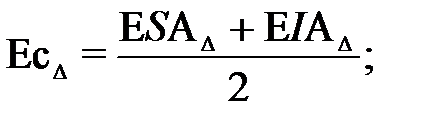
Зная координату середины поля допуска и допуск рассчитывают предельные отклонения замыкающего звена:

                                         ;                                   

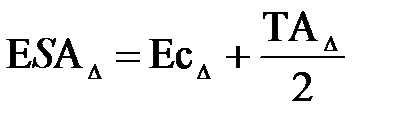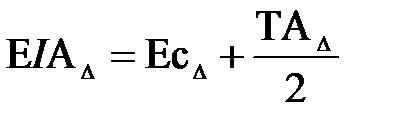
Рассмотрим решение размерной цепи методом полной взаимозаменяемости на конкретном примере. Решаем прямую задачу.

Исходные данные A_∆ = 2 ^+0,45.

1.Составляем схему размерной цепи (по сборочному чертежу машины или узла)

1. Выявляем увеличивающие и уменьшающие звенья.

А_1ум.,     А_2ув., А_3ув.

2. Записываем параметры замыкающего звена:

- номинальное значение A_∆ = 2мм;    

- предельные отклонения ESA_∆ = +450мкм, EIA_∆ = 0мкм;

- координата середины поля допуска

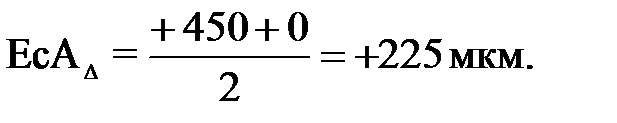
3. Устанавливаем (назначаем) номинальные значения всех составляющих звеньев (по сборочному чертежу с учетом масштаба).

А₁ = 108 мм; А₂ = 40 мм; А₃ =70 мм.

4. Проверяем правильность назначения номинальных размеров по уравнению размерной цепи в номиналах.

A _∆ = Σ A _{і ув.} - Σ A _{і ум.}                                                                                   (1)

или

                                    A_∆ = (A_{2 ув.}  + A_{3 ув.}) – A_{1 ум.}

                                   2 = (40 +70) – 108 = 2 мм,

т.е. номинальные значения составлены правильно.

5. Определяем среднюю величину допуска из уравнения:

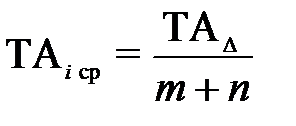 ,                                                                               (2)

где m – количество увеличивающих звеньев цепи,

                n – количество уменьшающих звеньев.

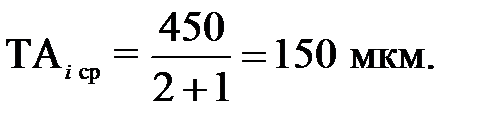
6. На все звенья, кроме одного (А₁) по таблице допусков назначаем стандартные допуски близкие к расчетному среднему значению ТА_іср.=150 мкм с учетом номинальных значений:  ТА₂ = 160 мкм, ТА₃ = 120 мкм.

7. На звено А₁ назначаем нестандартный допуск, используя уравнение (3)

ТА_∆ = Σ ТА _i                                                                                                     (3)

                                    ТА_∆ = ТА₁ + ТА₂ + ТА₃                                                                     

450 = ТА₁ + 160 + 120;       ТА₁ = 170 мкм.

9. Для охватывающих звеньев допуск задается в «+»,как для основного отверстия (Н), а для охватываемых в «-», как для основного вала (h). Для размеров деталей типа ступеней в «±» (Js).

Считаем, что А₂ и А₃ – охватывающие звенья (при отсутствии сборочного чертежа условнопринимаем задание допуска для увеличивающих звеньев в «+», а уменьшающих в «-»), записываем номинальные значения с отклонениями для второго и третьего звена (кроме звена А₁):

А₂ = 40^+0,16; А₃ = 70^+0,12.

10. Определяем координаты середин полей допусков составляющих звеньев кроме звена А_1.

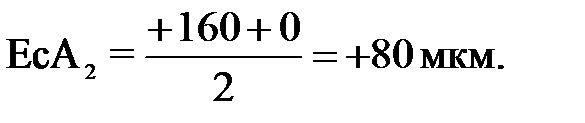
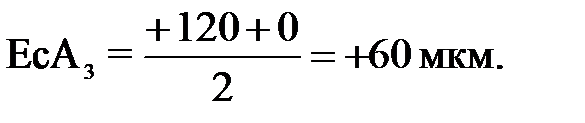
11. Координату середины поля допуска звена А₁ определяем из уравнения.

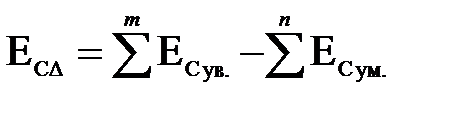                                                       (4) 

Е_сА_∆ = (Е_сА₂ + Е_сА₃) - Е_сА₁;

+225 = (+80) + (+60) - Е_сА₁; Е_сА₁ = +140 – 225 = -85 мкм.

12. Предельные отклонения звена А₁

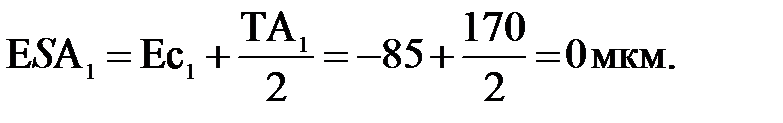
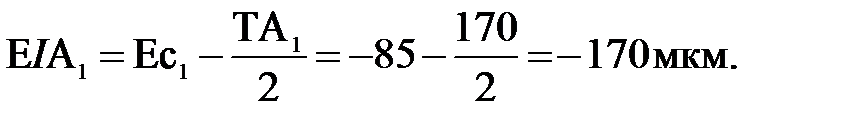
Записываем номинальное значение звена А₁ с найденными предельными отклонениями: А₁ = 108 _-0,17.

13. Проверку правильности расчетов выполняем по формулам

                                 .

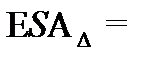
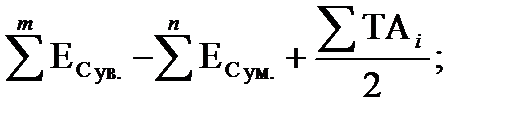
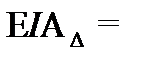
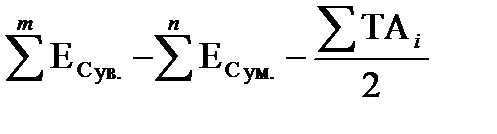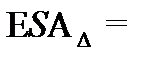
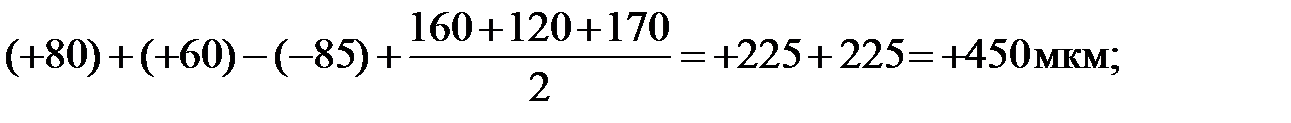
EIA_∆ =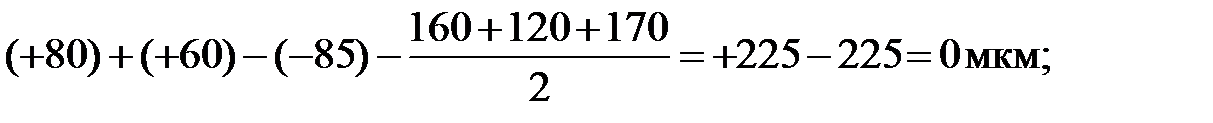

Проверка показала, что расчетные значения предельных отклонений замыкающего звена равны исходным, следовательно задача решена верно.